의학 통계 코드 저장소

[SAS] 도수분포표 (Frequency table), 분할표 (Contingency table) 만들기 - PROC FREQ

 수천 명의 정보를 포함한 데이터를 한눈에 요약하고 싶을 때가 많다. 나이, 혈압과 같은 연속형 변수는 평균으로 요약하곤 하는데, 성별이나 음주 여부는 평균을 구할 수 없으니 빈도를 제시하곤 한다. 이를 표로 제시하면 도수분포표 (Frequency table)가 된다. 이를 넘어서 남성 중 음주자가 몇 명인지, 여성중 비음주자가 몇 명인지 알고 싶을 때가 있는데, 이때 사용하는 것이 분할표 (Contingency table)이다. 즉 본 글의 목적은 다음 두 개의 표 내용을 채우는 것이다.

<도수분포표>

<분할표>

*실습용 데이터는 아래 링크를 클릭하면 다운로드할 수 있습니다.

2022.08.04 - [공지사항 및 소개] - 분석용 데이터 (update 22.08.18)

시작하기 위해 라이브러리를 만들고, 파일을 불러온다.

라이브러리 만드는 방법: 2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 라이브러리 만들기 - LIBNAME

파일 불러오는 방법: 2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 데이터 불러오기 및 저장하기 - PROC IMPORT, PROC EXPORT

*라이브러리 지정하기;
LIBNAME hong "C:/Users/User/Documents/Tistory_blog";

*파일 불러오기;
PROC IMPORT
DATAFILE="C:\Users\user\Documents\Tistory_blog\Data.xlsx"
DBMS=EXCEL
OUT=hong.df
REPLACE;
RUN;

코드

성별과 음주 여부의 분할표를 만드는 코드는 다음과 같다.

-변수

 1) SEX: 성별

  -0: 여성

  -1: 남성

 2) ALCOHOL: 음주 여부

  -0: 비음주자

  -1: 음주자

도수분포표 

PROC FREQ DATA=hong.df; 
TABLE SEX;
RUN;

PROC FREQ DATA=hong.df; : 도수분포표를 구하는 코드를 시작하며, 데이터는 hong 라이브러리 내의 df 파일을 사용한다.
TABLE SEX; : SEX의 도수분포표를 구하라

결과

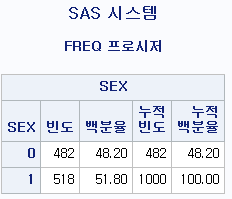
 위 결과에 숫자가 너무 많아 지저분해 보이고, 한눈에 잘 들어오지 않을 수 있다. 그런 경우 다음과 같은 옵션을 통해 표시되는 숫자들을 제어할 수 있다.

 NOPERCENT: 백분율 표시 안 함

 NOCUM: 누적 빈도 및 누적 백분율 표시 안 함

PROC FREQ DATA=hong.df; 
TABLE SEX/ NOCUM ;
RUN;

결과

분할표 

PROC FREQ DATA=hong.df; 
TABLE SEX*ALCOHOL;
RUN;

PROC FREQ DATA=hong.df; : 분할표를 구하는 코드를 시작하며, 데이터는 hong 라이브러리 내의 df 파일을 사용한다.
TABLE SEX*ALCOHOL; : SEX와 ALCOHOL 변수로 분할표를 만들어라.

 - *표시 앞에 오는 변수가 세로축에, 뒤에 오는 변수가 가로축에 놓이게 된다.

결과

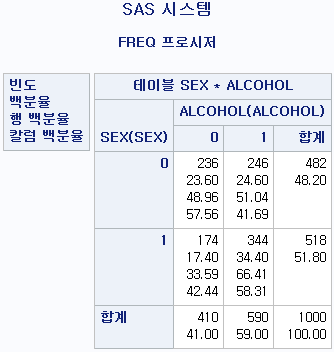
각 셀 안의 내용물은 다음과 같다

(1) 빈도 - 각 셀에 해당하는 인구의 수

(2) 백분율 - 빈도를 전체 인구 (1,000)으로 나눠 %로 나타낸 값

세로 혹은 가로로 더하면 합계의 백분율과 일치하며 백분율의 총합은 100과 같다.

(3) 행 백분율 - 각 행에서 빈도가 차지하는 분율.

 - 여성에서 비음주자가 차지하는 분율은 48.96%, 음주자가 차지하는 분율은 51.04%다.

 - 남성에서 비음주자가 차지하는 분율은 33.59%, 음주자가 차지하는 분율은 66.41%다.

따라서 행별로 더하면 (=같은 색깔끼리 더하면) 100%가 나오게 된다.

(4) 칼럼 백분율 - 각 열(칼럼)에서 빈도가 차지하는 분율.

 - 비음주자에서 여성이 차지하는 분율은 57.56%, 남성이 차지하는 분율은 42.44%다.

 - 음주자에서 여성이 차지하는 분율은 41.69%, 남성이 차지하는 분율은 58.31%다.

따라서 열(칼럼) 별로 더하면 (=같은 색깔끼리 더하면) 100%가 나오게 된다.

 위 결과에 숫자가 너무 많아 지저분해 보이고, 한눈에 잘 들어오지 않을 수 있다. 그런 경우 다음과 같은 옵션을 통해 표시되는 숫자들을 제어할 수 있다.

 NOFREQ: 빈도 표시 안 함 

 NOPERCENT: 백분율 표시 안 함

 NOROW: 행 백분율 표시 안 함

 NOCOL: 열(칼럼) 백분율 표시 안 함

PROC FREQ DATA=hong.df; 
TABLE SEX*ALCOHOL / NOPERCENT NOROW NOCOL;
RUN;

결과

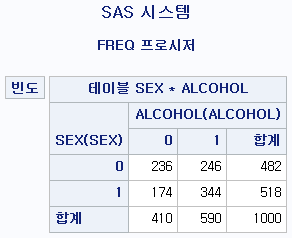
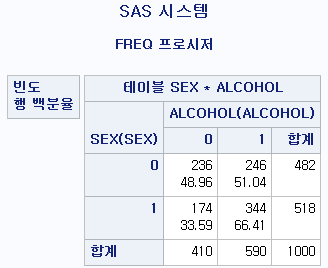
PROC FREQ DATA=hong.df; 
TABLE SEX*ALCOHOL / NOPERCENT NOCOL;
RUN;

결과

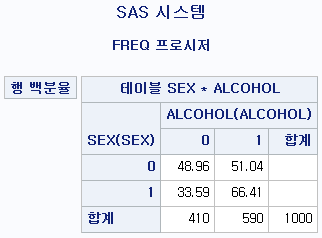
PROC FREQ DATA=hong.df; 
TABLE SEX*ALCOHOL / NOFREQ NOPERCENT NOCOL;
RUN;

결과

세 개 이상의 변수를 사용하는 분할표

세 개 이상의 변수를 사용하여 분할표를 작성하고 싶을 때가 있다. 다음 두 경우를 생각해보도록 하겠다.

1) 두 가지의 분할표를 작성하는 경우

:성별-음주의 분할표와 성별-고혈압의 분할표를 각각 그리고자 할 때

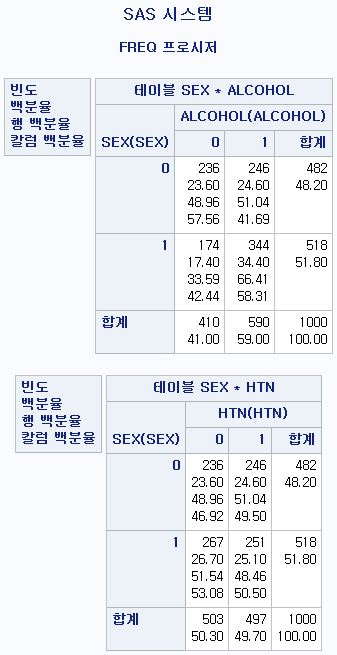
*방법 1: TABLE 구문 안에 원하는 변수의 조합을 모두 쓴다;
PROC FREQ DATA=hong.df; 
TABLE SEX*ALCOHOL SEX*HTN;
RUN;

*방법 2: 공통변수로 묶은 뒤 괄호 안에 나머지 변수를 띄어쓰기로 구분하여 작성한다;
PROC FREQ DATA=hong.df; 
TABLE SEX*(ALCOHOL HTN);
RUN;

두 개의 코드는 완벽히 똑같은 결과를 제시해준다. 

결과

2) 조건에 따라 분할표를 작성하는 경우

:고혈압 여부에 따른 성별-음주의 분할표를 그리고자 할 때

PROC FREQ DATA=hong.df; 
TABLE HTN*SEX*ALCOHOL;
RUN;

문제 상황처럼 고혈압 여부(HTN)에 따른 성별(SEX)과 음주(ALCOHOL)의 분할표를 그리고자 한다면, 고혈압 여부(HTN)를 TABLE구문 맨 앞에 추가로 붙여준다. 시행하면 다음과 같은 결과를 얻는다.

결과

고혈압이 없는 (HTN=0) 사람의 성별-음주 분할표가 위에 나오고, 고혈압이 있는 (HTN=1) 사람의 성별-음주 분할표가 따라 나오게 된다. 

 - SAS를 조금 아는 사람이라면 "WHERE 구문을 쓰면 되는데 왜 이렇게 복잡하게 하냐?"라고 이야기할 수도 있지만, 국민건강 영양조사(NHANES, KNHANES) 자료를 쓸 때엔 WHERE 구문이나 BY 구문의 사용이 엄격하게 금지되므로 이 방법이 필수적이다. 물론 이땐 PROC FREQ이 아니라 PROC SURVEYFREQ을 사용하게 된다.

 - SAS에는 인구를 나누는 변수를 맨 앞에 쓰지만, R에서는 맨 뒤에 쓴다는 것을 유의해야 한다.

SAS 도수분포표, 분할표 정복 완료!

작성일: 2022.08.18.

최종 수정일: 2022.08.31.

이용 프로그램: SAS v9.4

운영체제: Windows 10

[SPSS] 고급 Q-Q Plot - Van der Waerden, Rankit, Tukey, Blom

다음 글을 읽고 와야 이해하기 편하므로 먼저 읽고 올 것을 권한다.

2022.08.12 - [통계 이론] - [이론] Q-Q Plot (Quantile-Quantile Plot)

Q-Q Plot의 이론에서 상대적 위치를 대칭적으로 정하는 방법이 여럿 있다고 언급했다. 본 글에서는 특정 방법을 지정하여 Q-Q Plot을 그리는 법에 대해 소개하겠다.

*실습용 데이터는 아래 링크를 클릭하면 다운로드할 수 있습니다.

2022.08.04 - [공지사항 및 소개] - 분석용 데이터 (update 22.08.29)

데이터를 불러오도록 하겠다. 데이터를 불러오는 방법은 다음 링크에서 확인할 수 있다.

2022.08.04 - [통계 프로그램 사용 방법/SPSS] - [SPSS] 데이터 불러오기 및 저장하기

1) 분석(A) > 기술통계량(E) > Q-Q 도표...

2) 분석하고자 하는 변수 (ALT)를 오른쪽으로 넘긴다.

*검정분포(T), 분포모수, 변환은, 등순위에 부여되는 순위의 설정은 변경하지 않는다.

3)비율추정 공식에서 원하는 방식을 선택한다.

결과

1) Van der Waerden

2) Rankit

3) Tukey

4) Blom

 지금까지의 결과를 보면 알겠지만, 그림의 차이를 찾아볼 수 없을 정도로 거의 동일하다. 이렇게 $n$수가 충분하면 어떤 방법을 고르든 거의 똑같은 결과를 내주므로 적용할 방법에 대해 크게 연연할 필요가 없다.

[SPSS] 고급 Q-Q Plot 정복 완료!

작성일: 2022.08.18.

최종 수정일: 2022.09.06.

이용 프로그램: IBM SPSS v26

운영체제: Windows 10

[R] 고급 Q-Q Plot - Van der Waerden, Rankit, Tukey, Blom

다음 글을 읽고 와야 이해하기 편하므로 먼저 읽고 올 것을 권한다.

2022.08.12 - [통계 이론] - [이론] Q-Q Plot (Quantile-Quantile Plot)

Q-Q Plot의 이론에서 상대적 위치를 대칭적으로 정하는 방법이 여럿 있다고 언급했다. 본 글에서는 R에서 권하는 방법이 아니라, 특정 방법을 지정하여 Q-Q Plot을 그리는 법에 대해 소개하겠다.

코드를 보여드리기에 앞서 워킹 디렉토리부터 지정하겠다.

워킹 디렉토리에 관한 설명은 다음 링크된 포스트에서 볼 수 있다.

2022.08.05 - [통계 프로그램 사용 방법/R] - [R] 작업 디렉토리 (Working Directory) 지정 - getwd(), setwd()

setwd("C:/Users/user/Documents/Tistory_blog")

*실습용 데이터는 아래 링크를 클릭하면 다운로드할 수 있습니다.

2022.08.04 - [공지사항 및 소개] - 분석용 데이터 (update 22.08.10)

데이터를 불러와 a에 객체로 저장하겠다.

데이터 불러오는 방법은 다음 링크에서 볼 수 있다.

2022.08.05 - [통계 프로그램 사용 방법/R] - [R] 데이터 불러오기 : EXCEL - read_excel(), read.xlsx()

2022.08.08 - [통계 프로그램 사용 방법/R] - [R] 데이터 불러오기 : CSV - read_csv(), read.csv(), fread()

2022.08.10 - [통계 프로그램 사용 방법/R] - [R] 데이터 불러오기 : SAS file (.sas7bdat) - read.sas7bdat(), read_sas()

install.packages("readr")
library("readr")
a<-read_csv("Data.csv")

1) Van der Waerden 방법

Van der Waerden방법은 $\frac{k}{n+1}$이라는 수식을 사용한다.

코드

ALT_Data<-sort(a$ALT)
QQ_Van<-(c(1:length(ALT_Data)))/(length(ALT_Data)+1)
Z_Van<-qnorm(QQ_Van,0,1)
plot(Z_Van,ALT_Data)

ALT_Data<-sort(a$ALT) : a라는 데이터셋의 ALT 변수를 가져와 오름차순으로 정렬하여 ALT_Data에 저장한다.
QQ_Van<-(c(1:length(ALT_Data)))/(length(ALT_Data)+1) : Van der Waerden 수식의 $n$에 해당하는 데이터셋의 수를 의미한다. 우리 데이터에는 1,000명의 정보가 있으므로, 이는 1,000와 같다.

QQ_Van<-(c(1:length(ALT_Data)))/(length(ALT_Data)+1) : 1부터 1,000까지 1,001로 나누어 이를 QQ1에 저장한다.

Z_Van<-qnorm(QQ_Van,0,1) : 정규분포 상 $-\infty$부터 적분했을 때 QQ1의 각 값과 같아지는 $Z$값들을 구해 Z1에 저장한다.
plot(Z_Van,ALT_Data) : Z1과 ALT_Data로 plot을 그린다.

결과

2) Rankit 방법

Rankit 방법은 $\frac{k-\frac{1}{2}}{n}$이라는 수식을 사용한다.

코드

ALT_Data<-sort(a$ALT)
QQ_Rankit<-(c(1:length(ALT_Data))-1/2)/length(ALT_Data)
Z_Rankit<-qnorm(QQ_Rankit,0,1)
plot(Z_Rankit,ALT_Data)

결과

3) Tukey 방법

Tukey 방법은 $\frac{k-\frac{1}{3}}{n+\frac{1}{3}}$이라는 수식을 사용한다.

코드

ALT_Data<-sort(a$ALT)
QQ_Tukey<-(c(1:length(ALT_Data))-1/3)/(length(ALT_Data)+1/3)
Z_Tukey<-qnorm(QQ_Tukey,0,1)
plot(Z_Tukey,ALT_Data)

결과

4) Blom 방법

Blom 방법은 $\frac{k-\frac{3}{8}}{n+\frac{1}{4}}$이라는 수식을 사용한다.

코드

ALT_Data<-sort(a$ALT)
QQ_Blom<-(c(1:length(ALT_Data))-3/8)/(length(ALT_Data)+1/4)
Z_Blom<-qnorm(QQ_Blom,0,1)
plot(Z_Blom,ALT_Data)

결과

 지금까지의 결과를 보면 알겠지만, 그림의 차이를 찾아볼 수 없을 정도로 거의 동일하다. 이렇게 $n$수가 충분하면 어떤 방법을 고르든 거의 똑같은 결과를 내주므로 적용할 방법에 대해 크게 연연할 필요가 없다.

[R] 고급 Q-Q Plot 정복 완료!

작성일: 2022.08.16.

최종 수정일: 2022.08.16.

이용 프로그램: R 4.1.3

RStudio v1.4.1717

RStudio 2021.09.1+372 "Ghost Orchid" Release 

운영체제: Windows 10, Mac OS 10.15.7

[이론] 카이 제곱 검정 (Chi-squared test)

 범주형 자료의 분포에 유의미한 차이가 있는지 검정하기 위해 카이 제곱 검정 (Chi-squared test)를 시행하곤 한다. 깊은 이야기를 하기 전에 이번 글에서는 카이 제곱 검정 계산이 실제로 어떻게 시행되고, 자유도의 개념이 왜 존재하는지에 대해 다뤄보고자 한다.

 어떤 동네의 주민 1,000명의 흡연 여부, 폐암 여부에 따른 분포(관찰 빈도)가 다음과 같다고 하자. 

이 표를 보고 폐암 환자가 더 많다고 할 수 있는지에 대한 검정이 카이 제곱 검정이다. 카이 제곱 검정을 하는 과정은 다음과 같다.

1) 기대 빈도 산출

2) 카이 제곱 검정량 산출

3) 자유도 산출

4) p-value 계산

1) 기대 빈도 산출

카이 제곱 검정의 시작점은 "총합"이 정해져 있다고 하는데서부터 시작한다. 

 폐암 환자는 200명, 정상인은 800명, 흡연자는 300명, 비흡연자는 700명이라는 사실은 변하지 않는다고 생각하는 것이다. 이때 흡연자이자 폐암 환자인 사람은 몇 명이라고 예상하는 것이 합당할까? 다시 말하면, 흡연과 폐암이 아무 관련성이 없다면 (A)에는 몇 명이 있다고 예측하는 것이 합리적일까?

 폐암 환자는 200명이다. 또한 전체 인구 중 흡연자는 30%를 차지한다 (1,000명 중 300명). 따라서 200명의 30%인 60명이 흡연자가 될 것이라고 생각할 수 있다.  이런 식으로 기대 빈도 표를 모두 채우면 다음과 같다.

2) 카이 제곱 검정량 산출

관찰 빈도에서 기대 빈도 값을 뺀다.

각 값을 제곱한다.

각 값을 기대 빈도로 나눈다.

네 개의 값을 모두 더하면 카이 제곱 통계량이 된다.

$$카이 제곱 검정량=\frac{\left(75-60\right)^{2}}{60}+\frac{\left(225-240\right)^{2}}{240}+\frac{\left(125-140\right)^{2}}{140}+\frac{\left(6575-560\right)^{2}}{560}=6.6964$$

이 값을 잘 생각해보면, 관찰 빈도와 기대 빈도의 차이가 클수록 카이 제곱 검정량이 커진다는 것을 알 수 있다. 즉, 아무 관련성이 없다고 가정했을 때 예상되는 기대 빈도보다 더 많은 양이 관찰되거나, 훨씬 적은 양이 관찰된다면 카이 제곱 검정량이 커진다는 것이다. 따라서 너무나도 당연한 소리지만, 카이 제곱 검정량이 클수록 예상하지 못했던 결과라는 뜻이고, 유의미한 관련성이 있다는 뜻이다. 

 (따라서, 카이 제곱 검정량이 클수록 p-value가 작아지는 방식의 디자인이 필요하다.)

3) 자유도 산출

$$자유도=\left(열의\ 개수 - 1 \right)\times\left(행의\ 개수 - 1 \right)=1$$

4) p-value 계산

다음 두 가지 과정을 생각해보도록 한다.

 1) ɑ=0.05로 하였을 때 유의미한 관련성이 있다고 할 수 있는가?

자유도가 1인 카이 제곱 분포에서 카이 제곱 검정량이 0~3.84 사이일 때 적분 값이 0.95다. 즉, 아래 그림에서 빨간색 영역의 면적이 0.95, 파란색 영역의 면적이 0.05다. 따라서, 자유도가 1일 때, 카이 제곱 검정량이 0에서 3.84 사이로 관찰될 확률은 95%라는 뜻이고, 동시에 3.84 이상 관찰될 확률은 5%라는 뜻이다. 그러므로, 산출된 카이 제곱 검정량이 3.84보다 크면 유의미한 관련성이 있다는 것인데, 위 폐암-흡연의 카이 제곱 검정량은 6.6964였으므로 유의미한 관련성이 있다고 결론 내릴 수 있다.

[R] 위 그림 코드

x<-seq(0,10,0.001)
y<-dchisq(x,1)
plot(x,y,type="l",ann=FALSE, ylim=c(0,0.5))
title(main="Chi-Squared Distribution")
xrange<-seq(0,3.841458821,0.01)
funx<-dchisq(xrange,1)
polyx<-c(xrange,rev(xrange))
polyy<-c(rep(0,length(funx)),rev(funx))
polygon(polyx,polyy,col=2,border=NA)

xrange2<-seq(3.841458821,10,0.01)
funx2<-dchisq(xrange2,1)
polyx2<-c(xrange2,rev(xrange2))
polyy2<-c(rep(0,length(funx2)),rev(funx2))
polygon(polyx2,polyy2,col=4,border=NA)

2) 그래서 p-value가 몇인데?

0부터 산출된 카이 제곱 검정량인 6.6964까지의 자유도가 1인 카이 제곱 함수의 적분 값(아래 그림 초록색 영역)은 0.9903394이다. 따라서 p-value는 1에서 초록색 영역 넓이를 뺀 0.0097 (아래 그림 보라색 영역)이다. 즉, p-value는 산출된 카이 제곱 검정량에서부터의 카이 제곱 함수의 적분 값을 의미한다.

[R] 위 그림 코드

x<-seq(0,10,0.001)
y<-dchisq(x,1)
plot(x,y,type="l",ann=FALSE, ylim=c(0,0.5))
title(main="Chi-Squared Distribution")
xrange<-seq(0,6.696428571,0.01)
funx<-dchisq(xrange,1)
polyx<-c(xrange,rev(xrange))
polyy<-c(rep(0,length(funx)),rev(funx))
polygon(polyx,polyy,col=3,border=NA)

xrange2<-seq(6.696428571,10,0.01)
funx2<-dchisq(xrange2,1)
polyx2<-c(xrange2,rev(xrange2))
polyy2<-c(rep(0,length(funx2)),rev(funx2))
polygon(polyx2,polyy2,col=6,border=NA)

[R] p-value 산출 코드

1-pchisq(6.696428571,1)

그렇다면 카이 제곱 분포란 무엇인가?

카이 제곱 분포란 제곱한 정규분포의 합을 의미한다. 제곱한 정규분포를 여러 개 더할 수 있는데, 몇 개를 더했느냐가 자유도다.

$k$가 자유도, $Z$가 정규분포라면 카이 제곱 분포 $Q$는 다음과 같이 표현된다.

$$Q=\sum_{n=1}^k Z_{i}^{2}$$

이해할 수 있는 언어로 설명하기 위해 $k=1$인 상황을 가정하여 설명해 보겠다.

$$Q= Z^{2}$$

우리가 익히 알고 있는 정규분포에서 95%를 나타내는 범주는 [-1.96, 1.96]이다. 즉, 아래 그림에서 노란색 영역의 넓이는 0.95다.

[R] 위 그림 코드

x<-seq(-4,4,0.001)
y<-dnorm(x)
plot(x,y,type="l",ann=FALSE)
title(main="Normal Distribution")
xrange<-seq(-1.959964,1.959964,0.01)
funx<-dnorm(xrange)
polyx<-c(xrange,rev(xrange))
polyy<-c(rep(0,length(funx)),rev(funx))
polygon(polyx,polyy,col=7,border=NA)

카이 제곱은 정규분포를 제곱한다고 하였다. 

0은 0으로,

1은 1로,

2는 4로,

3은 9로, 

4는 16으로 이동한다.

음의 영역에서도

-1은 1로,

-2는 4로,

-3은 9로,

-4는 16으로 이동한다. 

즉 $x=0$이라는 직선을 기준으로 그래프를 반으로 접은 뒤에 양옆으로 잡아당긴 형태가 된다.

따라서 카이 제곱 분포의 그래프는 음의 영역이 존재하지 않는다.

그러면 위 그림의 노란색 영역은 어떻게 변할까?

1.96의 제곱도 3.84, -1.96의 제곱도 3.84이다.

[R] 위 그림 코드

x<-seq(-1.959964,1.959964,0.001)
y<-x^2
plot(x,y,type="l",ann=FALSE,xlim=c(-2,2),ylim=c(0,4))
par(new=TRUE)
x<-seq(-3,3,0.001)
y<-x*0+3.841458821
plot(x,y,type="l",col="red",ann=FALSE,xlim=c(-2,2),ylim=c(0,4))
par(new=TRUE)
y<-seq(-3,3.841458821,0.001)
x<-y*0-1.959964
plot(x,y,type="l",col="blue",ann=FALSE,xlim=c(-2,2),ylim=c(0,4))
par(new=TRUE)
y<-seq(-3,3.841458821,0.001)
x<-y*0+1.959964
plot(x,y,type="l",col="blue",ann=FALSE,xlim=c(-2,2),ylim=c(0,4))

따라서, 0에서 3.84까지 적분한 값이 0.95가 되는 아래와 같은 그래프일 것이다.

[R] 위 그림 코드

x<-seq(0,5,0.001)
y<-dchisq(x,1)
plot(x,y,type="l",ann=FALSE, ylim=c(0,0.5))
title(main="Chi-Squared Distribution")
xrange<-seq(0,3.841458821,0.01)
funx<-dchisq(xrange,1)
polyx<-c(xrange,rev(xrange))
polyy<-c(rep(0,length(funx)),rev(funx))
polygon(polyx,polyy,col=7,border=NA)

따라서, 일반적인 양수에 대해 다음의 두 등식이 성립한다.

[1] pnorm(a)=0.5*pchisq(a^2,1)+0.5
[2] pnorm(-a)+0.5*pchisq(a^2,1)+0.5=1

그런데 자유도는 왜 존재하는 개념인가?

우리는 위에서 폐암 환자는 200명, 정상인은 800명, 흡연자는 300명, 비흡연자는 700명이라는 사실이 변하지 않는다고 가정하고 논의를 이어갔다. 여기에서 만약 (A)가 100이라면 (B), (C), (D)의 값은 바로 100, 200, 600으로 정해진다. 우리가 "자유"로이 정할 수 있는 값은 (A), (B), (C), (D)중 단 한 개일 뿐이다. 따라서 자유도는 1이 된다.

자유도를 구하는 공식은 왜 $\left(열의\ 개수 - 1 \right)\times\left(행의\ 개수 - 1 \right)$인가?

 각 영역의 총합은 정해져 있으므로 "초등학교 졸업"영역에서 자유로이 정할 수 있는 것은 (A), (B), (C)중 두 개 뿐이다. 두 개의 값을 정하면 나머지 하나는 자연스럽게 정해지기 때문이다. 여기에서는 (A), (B)를 자유롭게 정했다고 하자.

 저체중 영역에서도 (A), (D), (G), (J) 중 세 개만 자유롭게 정할 수 있는데 (A), (D), (G)를 자유로이 정했다고 하자. 같은 방식으로 논리를 전개하면 자유롭게 정할 수 있는 값은 파란 색으로 표시된 6개 뿐이다. 즉, 열의 개수에서 1을 뺀 값과, 행의 개수에서 1을 뺀 값을 곱하여 자유도를 구할 수 있게 된다.

[이론] 카이 제곱 검정 (Chi-squared test) 정복 완료!

작성일: 2022.08.16.

최종 수정일: 2022.08.16.

이용 프로그램: R 4.1.3

RStudio v1.4.1717

RStudio 2021.09.1+372 "Ghost Orchid" Release 

운영체제: Windows 10, Mac OS 10.15.7

[이론] Q-Q Plot (Quantile-Quantile Plot)

정규성을 검정할 때 Q-Q Plot을 쓰곤 한다. 그런데 이런 궁금증이 들 수 있다.

왜 Q-Q Plot이 직선에 가까운 것이 정규성을 따른다는 뜻인가?

이에 대해 조목조목 설명해나갈 것이다.

먼저, 정규성을 따른다는 것이 어떤 의미인지 명확히 이해하고, 명확하게 설명할 수 있어야 한다.

정규성을 따른다는 것이 무엇인가?

정규성을 따른다는 것을 가장 쉽게 말하자면, 이는 히스토그램이 정규분포 곡선과 같이 종모양으로 생겼다는 것을 의미한다.

그렇다면 정규분포 곡선은 무엇을 의미하는가?

[사전 지식: 확률 밀도 함수의 그래프 아래 전체 면적은 1이다.]

어렵게 표현하자면 정규분포곡선은 정규분포의 확률 밀도 함수 (Probability Density Function, PDF)다. 그리고 확률 밀도 함수의 적분 값은 대상의 분율을 의미한다. 이해할 수 있는 언어로 표현하면 다음과 같다. 현실 세계에서 ALT의 분포는 정규분포를 따른다고 가정하자. 이때 아래 그림은 ALT의 분포를 나타낸 것이다. 여기에서 파란색으로 칠한 부분의 면적은 0.84인데 이 말은 전체 인구 중 84%의 ALT가 40 이하라는 뜻이다. 즉 전체 인구가 100명이라면 ALT 작은 순서대로 줄을 세웠을 때 84번째 서있는 사람의 ALT는 40이 된다.

  우리가 연구를 할 때 인구 전체를 대상으로 할 수는 없고 일부를 표본으로 뽑을 수밖에 없다. 설명을 용이하게 하기 위해 간단한 상황으로 전체 인구 중 3명을 뽑는 상황을 가정해보자. 누군가 ALT가 높거나 낮은 사람이 잘 뽑히도록 조작을 하지 않는 한 평균 정도에 있는 사람이 한 명, 평균 이하인 사람 중 한 명, 평균 이상인 사람 중 한 명이 뽑힐 것이라고 생각하는 것이 상식적이다. 

 위 그래프는 평균을 기준으로 대칭이므로 종 모양의 가장 높은 곳에 평균이 위치한다. 또한, 확률 밀도 함수 곡선 아래 면적은 1과 같으므로 아래 보라색 영역의 면적은 0.5와 같다. (평균은 35.1이다.)

 평균 이하인 사람 중 한 명은 어디에서 고르는 것이 합리적일까? 당연히 중간이다. 그런데 중간이 어디인지 어떻게 아는가? ALT의 최솟값이 19, 평균이 35이므로 두 값의 정중앙인 27로 골라야 하는가? 아니다. 평균 이하인 사람이 50명이라면 순서대로 줄을 세운 뒤 정중앙인 25번째에 서있는 사람을 골라야 한다. 줄을 세운 뒤 몇 등인지 확인하는 것은 정규분포 곡선 아래 면적을 구하는 것과 같으므로 왼쪽 끝에서부터 적분했을 때 0.25가 되는 ALT값을 찾아야 한다.  즉, 아래 그림에서 초록색 면적이 0.25가 되는 ALT값을 찾아야 한다. (이 ALT 값은 31.7이다)

평균 이상인 사람 중 한 명을 고르는 것도 같은 논리가 적용된다. 곡선 아래 면적이 0.75인 ALT값을 찾아야 한다. 즉, 아래 그림에서 노란색 면적이 0.75가 되는 ALT값을 찾아야 한다. (이 ALT 값은 38.5이다)

따라서 전체 인구 중 3명을 뽑았는데 그 ALT값이 각각 31.7, 35.1, 38.5였다면 정규분포를 따른다고 생각할 수 있다. (물론 이 예시는 3명이므로 당연히 정규분포를 따른다고 결론 내리는 것이 매우 부적절하다. 하지만 n수가 많다면 타당한 논리일 수 있다.) 

거꾸로 생각해보기

 그렇다면 위의 사전 지식이 없을 때 3명의 ALT 값이 각각 31.7, 35.1, 38.5였다면 이 값들이 정규분포를 따르는지 어떻게 확인할 수 있을까? 위의 과정을 그대로 거꾸로 쫓아가면 된다.

1) 데이터 줄세우고 상대적 위치 확인하기

ALT 값을 작은 순서대로 줄 세우면 31.7, 35.1, 38.5와 같다. 가장 작은 ALT값의 위치를 0, 가장 큰 ALT값의 위치를 1이라고 가정하면 중간의 35.1은 0.5에 위치한다고 볼 수 있고, 작은 값인 31.7은 0.25에 위치한다고 볼 수 있고, 큰 값인 38.5는 0.75에 위치한다고 볼 수 있다. 즉, 전체 인구가 100명이고 ALT가 정규분포를 따른다고 가정했을 때, 만약 25등의 ALT값이 31.7, 50등의 ALT값이 35.1, 75등의 ALT값이 38.5라면 3명의 데이터는 정규분포를 따른다고 생각할 수 있다.

2) 25등, 50등, 75등의 ALT값 확인하기

ALT의 평균은 35.1, 표준편차는 5.0이다. 그렇다면 평균이 35.1, 표준편차가 5.0인 정규분포 곡선을 그리고 왼쪽 끝에서부터 적분했을 때, 넓이가 0.25, 0.5, 0.75가 되는 ALT 값을 찾으면 된다. 그 값은 31.7, 35.1, 38.5이다. 이 위치는 정규분포를 따른다면 이론적으로 3명의 데이터가 위치해야 하는 곳을 의미한다.

3) [표본 3명의 ALT값]과 위에서 구한 [25등, 50등, 75등의 ALT값]을 비교하기

표본 3명의 ALT값은 31.7, 35.1, 38.5이고, 25등, 50등, 75등의 ALT값 이론적으로  31.7, 35.1, 38.5에 위치해야 한다. 실제 표본의 ALT값과 이론적인 값을 순서쌍으로 만들면 (31.7, 31.7), (35.1,35.1), (38.5, 38.5)다. 이를 좌표평면에 나타내면 일직선상에 존재하게 된다.

4) ALT의 평균과 표준편차를 모르는데?

 일반적으로, 우리가 표본을 뽑아 연구하는 이유는 모집단 전체를 대상으로 연구하기엔 시간과 돈이 많이 소비되기 때문이다. 따라서 모집단의 ALT 평균과 표준편차를 알 리가 없다. 이미 알고 있다면 연구할 필요가 없다. 이럴 때 어떻게 할 수 있을까? 평균이 0, 표준편차가 1인 표준 정규분포를 이용하면 된다. 표준 정규분포 곡선을 왼쪽 끝에서부터 적분했을 때, 넓이가 0.25, 0.5, 0.75가 되는 Z값을 찾으면 된다. 그 값은 각각 -0.67, 0, 0.67이다.

만약 모집단의 평균과 표준편차를 알고 있다면 다음 수식을 통해 이론적인 ALT 값(X)을 구할 수 있다.

$$Z=\frac{X-\mu}{\sigma}$$

 하지만, 정규성을 따지는데 굳이 이론적인 값까지 알 필요는 없다. 정규성을 따른다면 실제 값과 이론적인 값(X)이 일직선상에 존재한다는 것은 이미 위에서 밝혔다. 그런데 위 수식에 의거 이론적인 값(X)은 Z와 선형 관계에 있다. 따라서 실제 값 또한 Z와 선형 관계에 있다. 따라서 정규성을 따른다면 실제 값은 Z와 선형 관계를 띄기 때문에 일직선 상에 위치하게 된다. 이 점에 착안하여 실제 값과 Z의 plot을 그린 것이 Q-Q plot이다.

 또한 가로축에 Z, 세로축에 X를 놓는다면, 당연하게도 기울기는 $\sigma$가 된다.

실제 Q-Q plot 그릴 때 다를 수 있는 점

 여기까지 읽어본 독자 중 누군가는 Q-Q plot을 직접 그려보았을 수도 있다. (그리는 법은 다음 링크 참고:2022.08.11 - [기술 통계/R] - [R] 정규성 검정 (1) : QQplot - qqnorm(), qqline()) 그러면 위와 다른 그림을 그려주는 것을 확인할 수 있다.

코드

qq<-qqnorm(c(31.7, 35.1, 38.5))
identity(qq)

결과

$x
[1] -0.8694238  0.0000000  0.8694238

$y
[1] 31.7 35.1 38.5

x축 위치가 (-0.67, 0, 0.67)이 아니다! 왜 이런 일이 발생한 것일까?

필자는 3명의 상대적 위치를 0.25, 0.5, 0.75로 잡았다. 하지만 상대적 위치를 어디로 잡는 것이 좋은가에 대해서는 갑론을박이 있을 수 있으며 많은 방법론이 다음 표와 같이 존재한다. 필자는 이해를 돕기 위해 가장 간단한 첫 번째 방법 (Van der Waerden)을 사용하였다.

R에서는 n수가 10 이하일 때까지는 Blom의 방법을, 11부터는 Rankit의 방법을 사용한다. 

SPSS, R에서는 각각의 방법에 따라 Q-Q plot을 그릴 수 있다. 다음 링크에서 확인할 수 있다.

SPSS:

R:

[이론] Q-Q plot 정복 완료!

작성일: 2022.08.12.

최종 수정일: 2022.08.12.

이용 프로그램: R 4.1.3, RStudio v1.4.1717

운영체제: Windows 10

[SAS] 정규성 검정 - PROC UNIVARIATE

 많은 통계 분석에서 전제조건으로 데이터의 정규성(normality)을 요구하곤 한다. SAS로 정규성 검정을 하는 방법을 살펴보고자 한다.

라이브러리를 지정하고 데이터를 불러온다

라이브러리 지정 방법 :2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 라이브러리 만들기 - LIBNAME

데이터 불러오는 방법: 2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 데이터 불러오기 및 저장하기 - PROC IMPORT, PROC EXPORT

*라이브러리 지정하기;
LIBNAME hong "C:/Users/User/Documents/Tistory_blog";

*데이터 불러오기;
PROC IMPORT
DATAFILE="C:\Users\user\Documents\Tistory_blog\Data.xlsx"
DBMS=EXCEL
OUT=hong.df
REPLACE;
RUN;

코드

데이터 중 ALT라는 변수로 정규성을 검정하고자 할 때 코드는 다음과 같다.

PROC UNIVARIATE DATA=hong.df NORMAL PLOT;
VAR ALT;
HISTOGRAM ALT/ NORMAL (MU=EST SIGMA=EST);
RUN;

PROC UNIVARIATE : 변수에 대해 알아보는 코드를 작성하겠다.

DATA=hong.df : 데이터는 hong이라는 라이브러리 내에 있는 df를 사용하겠다.

NORMAL : 정규성 검정을 시행해라.

PLOT : 히스토그램과 QQ plot을 그려라
VAR ALT : 분석할 변수는 ALT다
HISTOGRAM ALT : ALT의 히스토그램도 그려라

/ NORMAL (MU=EST SIGMA=EST) : 히스토그램에 정규분포 곡선도 그리는데, 정규분포 곡선의 평균은 ALT 데이터로부터 계산한 평균이고, 표준편차도 ALT 데이터의 표준편차다.

1) Q-Q plot

결과

해석방법

데이터가 직선상에 있음: 정규성 따름

데이터가 직선에서 벗어나 있음: 정규성 따르지 않음

따라서, "대부분의 데이터들이 일직선 상에 있으므로 정규성을 따른다고 할 수 있다."

Q-Q plot 이론은 다음 링크에서 확인할 수 있다.

2022.08.12 - [통계 이론] - [이론] Q-Q Plot (Quantile-Quantile Plot)

2) 히스토그램

결과

해석 방법

히스토그램 막대가 정규분포 곡선 상에 있음: 정규성 따름

히스토그램 막대가 정규분포 곡선에서 벗어남: 정규성 따르지 않음

따라서, "대부분의 히스토그램 막대가 정규분포 곡선 상에 있으므로 정규성을 따른다고 할 수 있다."

3) 통계적 검정

결과

해석 방법

초급자: p-value>0.05이므로 정규성을 따른다.

중급자:

귀무 가설과 대립 가설은 다음과 같다.

-귀무 가설: ALT는 정규성을 따른다.

-대립 가설: ALT는 정규성을 따르지 않는다.

이때 제 1종 오류는 다음과 같다.

제 1종 오류

=귀무 가설이 참인데도 기각하고 대립 가설을 택함

=ALT는 정규성을 따르는데도 따르지 않는다고 결론 내림

p-value는 제 1종 오류를 범할 확률을 의미하므로 다음과 같이 결론 내릴 수 있다.

결론: 정규성을 따르는 것이 진실인데, 따르지 않는다고 결론 내렸을 확률이 0.05보다 크다.

=정규성을 따르는 것이 진실인데, 따르지 않는다고 결론 내린 것은 잘못일 수 있다.

=정규성을 따르지 않는다고는 할 수 없다.

고급자:

-본 데이터의 n 수는 1,000명으로 2,000명 미만이므로 Shapiro-Wilk test의 결과를 인용한다. (SAS 기준, 2,000명까지는 Shapiro-Wilk test을 계산해주고, Kolmogorov-Smirnov test는 2,000명 이상이 필요하다.)

-또한, QQplot과 히스토그램의 결과도 고려하여 정규성 여부를 판단해야 한다.

SAS 정규성 검정 정복 완료!

작성일: 2022.08.12.

최종 수정일: 2022.08.13.

이용 프로그램: SAS v9.4

운영체제: Windows 10

[R] 정규성 검정 (4) : 정량적 검정 (Lilliefors test) - lillie.test()

정규성 검정을 하는 방법은 지금까지 다룬 세 가지가 많이 쓰인다.

정규성 검정 방법

1) QQ plot : 2022.08.11 - [기술 통계/R] - [R] 정규성 검정 (1) : QQplot - qqnorm()

2) 히스토그램: 2022.08.11 - [기술 통계/R] - [R] 정규성 검정 (2) : 히스토그램 - hist(), dnorm()

3) 통계적 검정: 2022.08.11 - [기술 통계/R] - [R] 정규성 검정 (3) : 정량적 검정 (Shapiro-Wilk, Kolmogorov-Smirnov) - shapiro.test(), ks.test()

세 번째 방법인 통계적 검정에서 Kolmogorov-Smirnov test는 그대로 사용하지 않고 p-value만 교정한 Lilliefors test를 더 많이 사용한다. SPSS에서도 Lilliefors 교정된 Kolmogorov-Smirnov test 결과를 보여주는 것을 다음 링크에서 확인할 수 있다. 2022.08.11 - [기술 통계/SPSS] - [SPSS] 정규성 검정

그래서 이번에는 R에서 Lilliefors test를 하는 방법을 다뤄보고자 한다.

코드를 보여드리기에 앞서 워킹 디렉토리부터 지정하겠다.

워킹 디렉토리에 관한 설명은 다음 링크된 포스트에서 볼 수 있다.

2022.08.05 - [통계 프로그램 사용 방법/R] - [R] 작업 디렉토리 (Working Directory) 지정 - getwd(), setwd()

setwd("C:/Users/user/Documents/Tistory_blog")

*실습용 데이터는 아래 링크를 클릭하면 다운로드할 수 있습니다.

2022.08.04 - [공지사항 및 소개] - 분석용 데이터 (update 22.08.10)

데이터를 불러와 a에 객체로 저장하겠다.

데이터 불러오는 방법은 다음 링크에서 볼 수 있다.

2022.08.05 - [통계 프로그램 사용 방법/R] - [R] 데이터 불러오기 : EXCEL - read_excel(), read.xlsx()

2022.08.08 - [통계 프로그램 사용 방법/R] - [R] 데이터 불러오기 : CSV - read_csv(), read.csv(), fread()

2022.08.10 - [통계 프로그램 사용 방법/R] - [R] 데이터 불러오기 : SAS file (.sas7bdat) - read.sas7bdat(), read_sas()

install.packages("readr")
library("readr")
a<-read_csv("Data.csv")

Lilliefors test를 위해서는 "nortest" 패키지의 "lillie.test()"함수를 사용한다. 따라서 설치한 뒤 데이터의 변수 ALT로 lilliefors test를 시행하는 코드는 다음과 같다.

코드

install.packages("nortest")
library("nortest")
lillie.test(a$ALT)

결과

	Lilliefors (Kolmogorov-Smirnov) normality test

data:  a$ALT
D = 0.015397, p-value = 0.8184

Kolmogorov-Smirnov test결과와 D statistics 값은 0.015397로 같은데, p-value만 다르다는 것을 알 수 있다. (Kolmogorov-Smirnov test결과는 다음 링크에서 확인할 수 있다.2022.08.11 - [기술 통계/R] - [R] 정규성 검정 (3) : 정량적 검정 (Shapiro-Wilk, Kolmogorov-Smirnov) - shapiro.test(), ks.test())

해석방법

초급자: p-value>0.05이므로 정규성을 따른다.

중급자:

귀무 가설과 대립 가설은 다음과 같다.

-귀무 가설: ALT는 정규성을 따른다.

-대립 가설: ALT는 정규성을 따르지 않는다.

이때 제 1종 오류는 다음과 같다.

제 1종 오류

=귀무 가설이 참인데도 기각하고 대립 가설을 택함

=ALT는 정규성을 따르는데도 따르지 않는다고 결론 내림

p-value는 제 1종 오류를 범할 확률을 의미하므로 다음과 같이 결론 내릴 수 있다.

결론: 정규성을 따르는 것이 진실인데, 따르지 않는다고 결론 내렸을 확률이 0.05보다 크다.

=정규성을 따르는 것이 진실인데, 따르지 않는다고 결론 내린 것은 잘못일 수 있다.

=정규성을 따르지 않는다고는 할 수 없다.

고급자:

-본 데이터의 n 수는 1,000명으로 2,000명 미만이므로 Shapiro-Wilk test의 결과를 인용해야 한다. 따라서 본 결과는 신뢰하지 않는다.

-또한, QQplot과 히스토그램의 결과도 고려하여 정규성 여부를 판단해야 한다.

R 정규성 검정 (정량적 검정 - Lilliefors test) 정복 완료!

작성일: 2022.08.12.

최종 수정일: 2022.08.12.

이용 프로그램: R 4.1.3, RStudio v1.4.1717

운영체제: Windows 10

[SPSS] 정규성 검정

많은 통계 분석에서 전제조건으로 데이터의 정규성(normality)을 요구하곤 한다. SPSS로 정규성 검정을 하는 방법을 살펴보고자 한다.

*실습용 데이터는 아래 링크를 클릭하면 다운로드할 수 있습니다.

2022.08.04 - [공지사항 및 소개] - 분석용 데이터 (update 22.08.29)

먼저 데이터를 불러온다

(데이터 불러오는 방법은 다음 링크 참고:

2022.08.04 - [통계 프로그램 사용 방법/SPSS] - [SPSS] 데이터 불러오기 및 저장하기)

정규성 검정 방법

1) 분석 (A)>기술통계량 (E) > 데이터 탐색 (E)

2) 분석하고자 하는 변수를 "종속변수(D)" 쪽으로 이동

3) 도표(T)를 누르고, "히스토그램(H)", "검정과 함께 정규성도표(O)" 체크박스를 클릭. 다 되었으면 "계속(C)" 클릭

4) "확인" 을 눌러 결과 확인

1) Q-Q plot

R에서 그린 그림과 비교해보면 약간 다른데, x축과 y축이 바뀌어 있기 때문이다.

R로 그린 Q-Q plot은 다음 링크에서 확인할 수 있다: 2022.08.11 - [기술 통계/R] - [R] 정규성 검정 (1) : QQplot - qqnorm(), qqline() 

해석방법

데이터가 직선상에 있음: 정규성 따름

데이터가 직선에서 벗어나 있음: 정규성 따르지 않음

따라서, "대부분의 데이터들이 일직선 상에 있으므로 정규성을 따른다고 할 수 있다."

Q-Q plot 이론은 다음 링크에서 확인할 수 있다.

2022.08.12 - [통계 이론] - [이론] Q-Q Plot (Quantile-Quantile Plot)

2) 정량적 검정 (Shapiro-Wilk, Kolmogorov-Smirnov test) 

해석방법

초급자: p-value>0.05이므로 정규성을 따른다.

중급자:

귀무 가설과 대립 가설은 다음과 같다.

-귀무 가설: ALT는 정규성을 따른다.

-대립 가설: ALT는 정규성을 따르지 않는다.

이때 제 1종 오류는 다음과 같다.

제 1종 오류

=귀무 가설이 참인데도 기각하고 대립 가설을 택함

=ALT는 정규성을 따르는데도 따르지 않는다고 결론 내림

p-value는 제 1종 오류를 범할 확률을 의미하므로 다음과 같이 결론내릴 수 있다.

결론: 정규성을 따르는 것이 진실인데, 따르지 않는다고 결론내렸을 확률이 0.05보다 크다.

=정규성을 따르는 것이 진실인데, 따르지 않는다고 결론내린 것은 잘못일 수 있다.

=정규성을 따르지 않는다고는 할 수 없다.

고급자:

-(비록 본 데이터는 n수가 충분하지만) n수가 굉장히 적다면 정규성 검정을 잘 통과하므로 결과를 맹신해서는 안 된다.

-본 데이터의 n수는 1,000명으로 2,000명 미만이므로 Shapiro-Wilk test의 결과를 인용한다. (SAS 기준, 2,000명까지는 Shapiro-Wilk test을 계산해주고, Kolmogorov-Smirnov test는 2,000명 이상이 필요하다.)

-또한, QQplot과 히스토그램의 결과도 고려하여 정규성 여부를 판단해야 한다.

R에서 시행한 Kolmogorov-Smirnov test 결과와 약간 다르다. R의 Kolmogorov-Smirnov test결과는 다음 링크에서 확인할 수 있다.2022.08.11 - [기술 통계/R] - [R] 정규성 검정 (3) : 정량적 검정 (Shapiro-Wilk, Kolmogorov-Smirnov) - shapiro.test(), ks.test()

다르게 나타나는 이유는 두 가지가 있다.

1) SPSS 결과의 p-value "0.200*" 이란 ">0.2"를 의미한다. 즉 적어도 0.2보다는 크다는 뜻을 의미하며, R에서의 결과인 "0.9717"과는 그렇게 배치되는 이야기가 아니다. 

2) SPSS는 Lilliefors가 수정한 방식의 유의확률을 계산해준다. 초창기에 만든 Kolmogorov-Smirnov test는 모종의 문제가 있어 Lilliefors가 p-value를 수정하게 되었다. SPSS는 이를 제시해주고 있다. R에서 Lilliefors가 수정한 Kolmogorov-Smirnov test를 하는 방법은 다음 링크에서 확인할 수 있다.

3) 히스토그램

히스토그램은 이렇게 그려주는데 정규분포 곡선이 그려져있지 않다. 이를 위해서는 다음의 단계를 거쳐 새로 그려야 한다.

1) 그래프(G)>레거시 대화 상자 (L)> 히스토그램 (I)

2) 분석하고자 하는 변수를 "변수(V):"쪽으로 옮기고, "정규곡선 표시(D)" 체크박스에 체크를 한다. 그리고 "확인"을 누른다.

결과

해석방법

히스토그램 막대가 정규분포 곡선 상에 있음: 정규성 따름

히스토그램 막대가 정규분포 곡선 에서 벗어남: 정규성 따르지 않음

따라서, "대부분의 히스토그램 막대가 정규분포 곡선 상에 있으므로 정규성을 따른다고 할 수 있다."

SPSS 정규성 검정 정복 완료!

작성일: 2022.08.11.

최종 수정일: 2022.11.29.

이용 프로그램: IBM SPSS v26

운영체제: Windows 10