
[이론] 카이 제곱 검정 (Chi-squared test)
범주형 자료의 분포에 유의미한 차이가 있는지 검정하기 위해 카이 제곱 검정 (Chi-squared test)를 시행하곤 한다. 깊은 이야기를 하기 전에 이번 글에서는 카이 제곱 검정 계산이 실제로 어떻게 시행되고, 자유도의 개념이 왜 존재하는지에 대해 다뤄보고자 한다.
어떤 동네의 주민 1,000명의 흡연 여부, 폐암 여부에 따른 분포(관찰 빈도)가 다음과 같다고 하자.
| 관찰 빈도 | 흡연자 | 비흡연자 | 총합 |
| 폐암 환자 | 75 | 125 | 200 |
| 정상인 | 225 | 575 | 800 |
| 총합 | 300 | 700 | 1000 |
이 표를 보고 폐암 환자가 더 많다고 할 수 있는지에 대한 검정이 카이 제곱 검정이다. 카이 제곱 검정을 하는 과정은 다음과 같다.
1) 기대 빈도 산출
2) 카이 제곱 검정량 산출
3) 자유도 산출
4) p-value 계산
1) 기대 빈도 산출
카이 제곱 검정의 시작점은 "총합"이 정해져 있다고 하는데서부터 시작한다.
| 흡연자 | 비흡연자 | 총합 | |
| 폐암 환자 | (A) | 200 | |
| 정상인 | 800 | ||
| 총합 | 300 | 700 | 1000 |
폐암 환자는 200명, 정상인은 800명, 흡연자는 300명, 비흡연자는 700명이라는 사실은 변하지 않는다고 생각하는 것이다. 이때 흡연자이자 폐암 환자인 사람은 몇 명이라고 예상하는 것이 합당할까? 다시 말하면, 흡연과 폐암이 아무 관련성이 없다면 (A)에는 몇 명이 있다고 예측하는 것이 합리적일까?
폐암 환자는 200명이다. 또한 전체 인구 중 흡연자는 30%를 차지한다 (1,000명 중 300명). 따라서 200명의 30%인 60명이 흡연자가 될 것이라고 생각할 수 있다. 이런 식으로 기대 빈도 표를 모두 채우면 다음과 같다.
| 기대 빈도 | 흡연자 | 비흡연자 | 총합 |
| 폐암 환자 | 60 | 140 | 200 |
| 정상인 | 240 | 560 | 800 |
| 총합 | 300 | 700 | 1000 |
2) 카이 제곱 검정량 산출
관찰 빈도에서 기대 빈도 값을 뺀다.
| 관찰 빈도-기대 빈도 | 흡연자 | 비흡연자 |
| 폐암 환자 | $75-60$ | $125-140$ |
| 정상인 | $225-240$ | $575-560$ |
각 값을 제곱한다.
| $\left(관찰 빈도-기대 빈도\right)^{2}$ | 흡연자 | 비흡연자 |
| 폐암 환자 | $\left(75-60\right)^{2}$ | $\left(125-140\right)^{2}$ |
| 정상인 | $\left(225-240\right)^{2}$ |
$\left(575-560\right)^{2}$ |
각 값을 기대 빈도로 나눈다.
| $\frac{\left(관찰 빈도-기대 빈도\right)^{2}}{기대 빈도}$ | 흡연자 | 비흡연자 |
| 폐암 환자 | $\frac{\left(75-60\right)^{2}}{60}$ | $\frac{\left(125-140\right)^{2}}{140}$ |
| 정상인 | $\frac{\left(225-240\right)^{2}}{240}$ | $\frac{\left(575-560\right)^{2}}{560}$ |
네 개의 값을 모두 더하면 카이 제곱 통계량이 된다.
$$카이 제곱 검정량=\frac{\left(75-60\right)^{2}}{60}+\frac{\left(225-240\right)^{2}}{240}+\frac{\left(125-140\right)^{2}}{140}+\frac{\left(6575-560\right)^{2}}{560}=6.6964$$
이 값을 잘 생각해보면, 관찰 빈도와 기대 빈도의 차이가 클수록 카이 제곱 검정량이 커진다는 것을 알 수 있다. 즉, 아무 관련성이 없다고 가정했을 때 예상되는 기대 빈도보다 더 많은 양이 관찰되거나, 훨씬 적은 양이 관찰된다면 카이 제곱 검정량이 커진다는 것이다. 따라서 너무나도 당연한 소리지만, 카이 제곱 검정량이 클수록 예상하지 못했던 결과라는 뜻이고, 유의미한 관련성이 있다는 뜻이다.
(따라서, 카이 제곱 검정량이 클수록 p-value가 작아지는 방식의 디자인이 필요하다.)
3) 자유도 산출
$$자유도=\left(열의\ 개수 - 1 \right)\times\left(행의\ 개수 - 1 \right)=1$$
4) p-value 계산
다음 두 가지 과정을 생각해보도록 한다.
1) ɑ=0.05로 하였을 때 유의미한 관련성이 있다고 할 수 있는가?
자유도가 1인 카이 제곱 분포에서 카이 제곱 검정량이 0~3.84 사이일 때 적분 값이 0.95다. 즉, 아래 그림에서 빨간색 영역의 면적이 0.95, 파란색 영역의 면적이 0.05다. 따라서, 자유도가 1일 때, 카이 제곱 검정량이 0에서 3.84 사이로 관찰될 확률은 95%라는 뜻이고, 동시에 3.84 이상 관찰될 확률은 5%라는 뜻이다. 그러므로, 산출된 카이 제곱 검정량이 3.84보다 크면 유의미한 관련성이 있다는 것인데, 위 폐암-흡연의 카이 제곱 검정량은 6.6964였으므로 유의미한 관련성이 있다고 결론 내릴 수 있다.
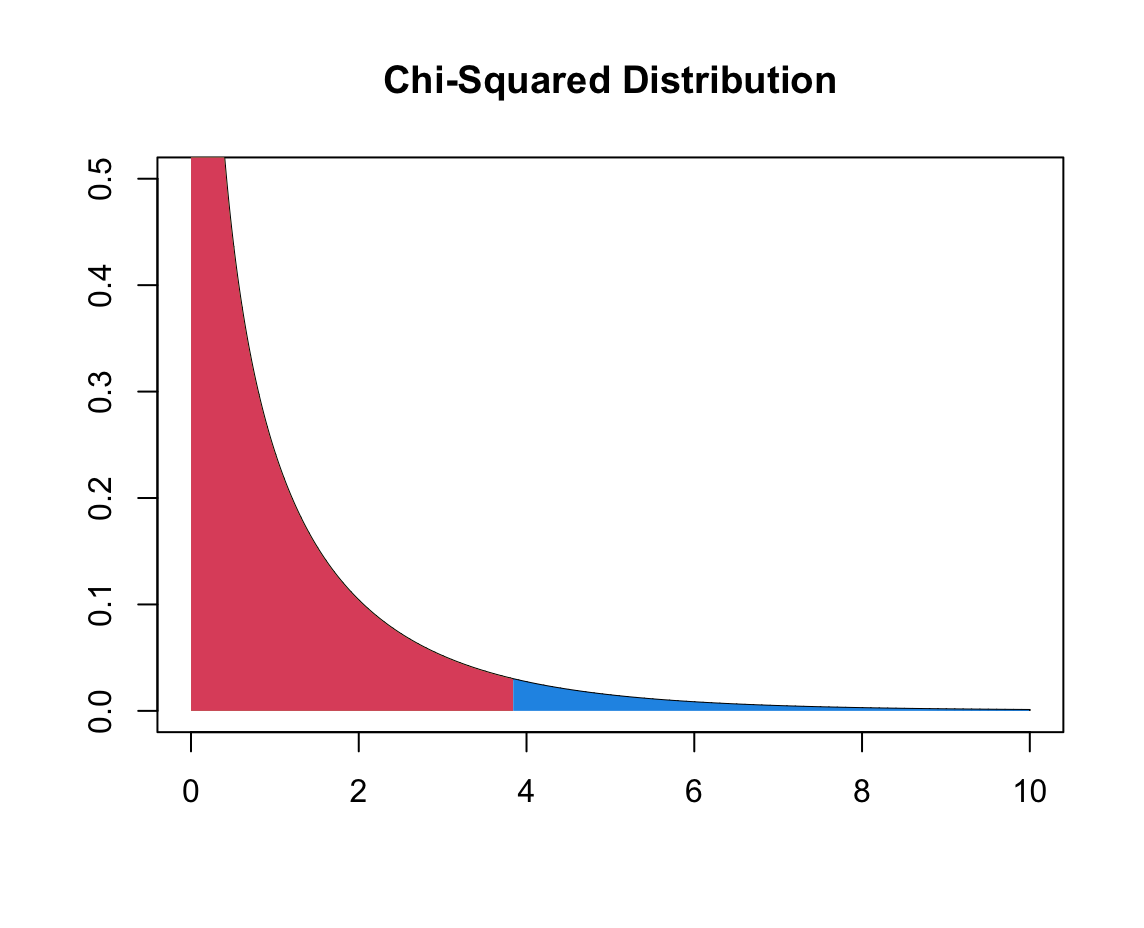
[R] 위 그림 코드
x<-seq(0,10,0.001)
y<-dchisq(x,1)
plot(x,y,type="l",ann=FALSE, ylim=c(0,0.5))
title(main="Chi-Squared Distribution")
xrange<-seq(0,3.841458821,0.01)
funx<-dchisq(xrange,1)
polyx<-c(xrange,rev(xrange))
polyy<-c(rep(0,length(funx)),rev(funx))
polygon(polyx,polyy,col=2,border=NA)
xrange2<-seq(3.841458821,10,0.01)
funx2<-dchisq(xrange2,1)
polyx2<-c(xrange2,rev(xrange2))
polyy2<-c(rep(0,length(funx2)),rev(funx2))
polygon(polyx2,polyy2,col=4,border=NA)
2) 그래서 p-value가 몇인데?
0부터 산출된 카이 제곱 검정량인 6.6964까지의 자유도가 1인 카이 제곱 함수의 적분 값(아래 그림 초록색 영역)은 0.9903394이다. 따라서 p-value는 1에서 초록색 영역 넓이를 뺀 0.0097 (아래 그림 보라색 영역)이다. 즉, p-value는 산출된 카이 제곱 검정량에서부터의 카이 제곱 함수의 적분 값을 의미한다.
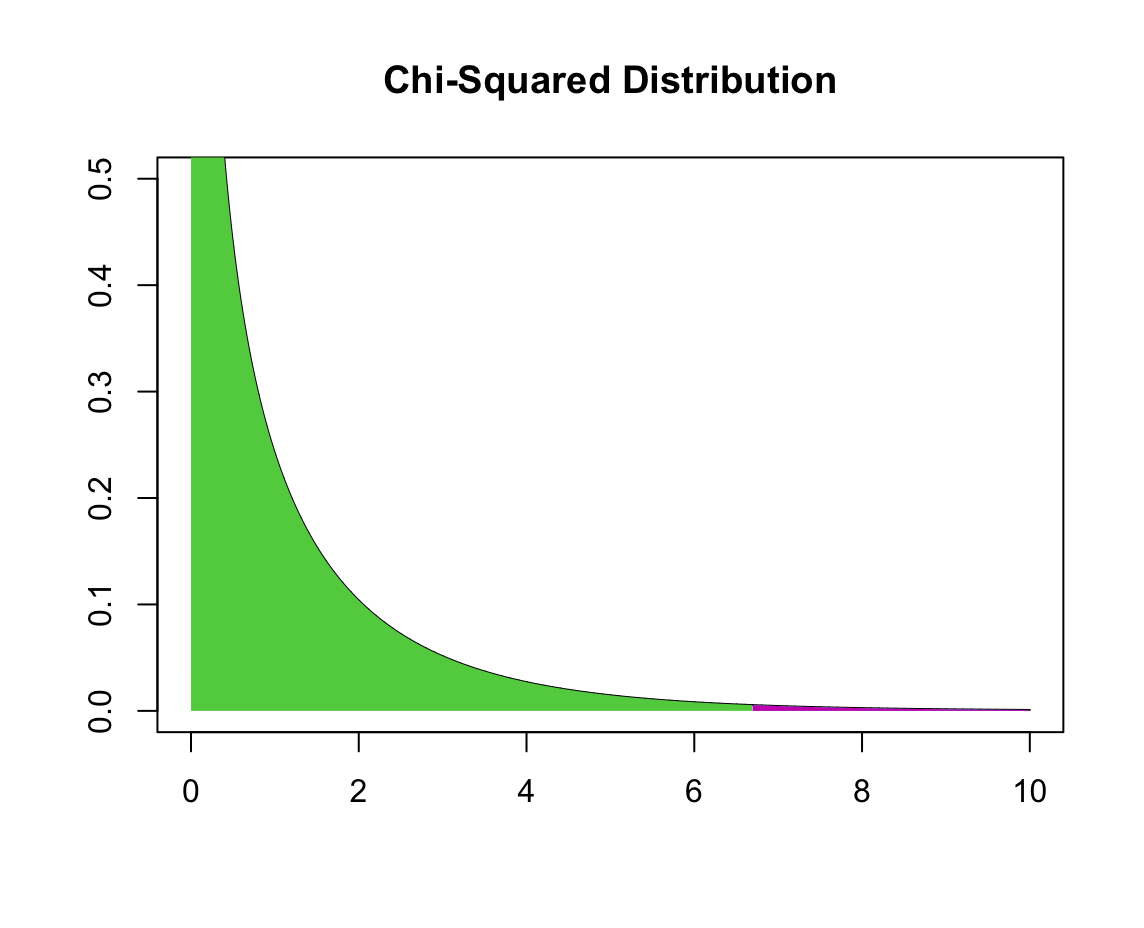
[R] 위 그림 코드
x<-seq(0,10,0.001)
y<-dchisq(x,1)
plot(x,y,type="l",ann=FALSE, ylim=c(0,0.5))
title(main="Chi-Squared Distribution")
xrange<-seq(0,6.696428571,0.01)
funx<-dchisq(xrange,1)
polyx<-c(xrange,rev(xrange))
polyy<-c(rep(0,length(funx)),rev(funx))
polygon(polyx,polyy,col=3,border=NA)
xrange2<-seq(6.696428571,10,0.01)
funx2<-dchisq(xrange2,1)
polyx2<-c(xrange2,rev(xrange2))
polyy2<-c(rep(0,length(funx2)),rev(funx2))
polygon(polyx2,polyy2,col=6,border=NA)
[R] p-value 산출 코드
1-pchisq(6.696428571,1)
그렇다면 카이 제곱 분포란 무엇인가?
카이 제곱 분포란 제곱한 정규분포의 합을 의미한다. 제곱한 정규분포를 여러 개 더할 수 있는데, 몇 개를 더했느냐가 자유도다.
$k$가 자유도, $Z$가 정규분포라면 카이 제곱 분포 $Q$는 다음과 같이 표현된다.
$$Q=\sum_{n=1}^k Z_{i}^{2}$$
이해할 수 있는 언어로 설명하기 위해 $k=1$인 상황을 가정하여 설명해 보겠다.
$$Q= Z^{2}$$
우리가 익히 알고 있는 정규분포에서 95%를 나타내는 범주는 [-1.96, 1.96]이다. 즉, 아래 그림에서 노란색 영역의 넓이는 0.95다.
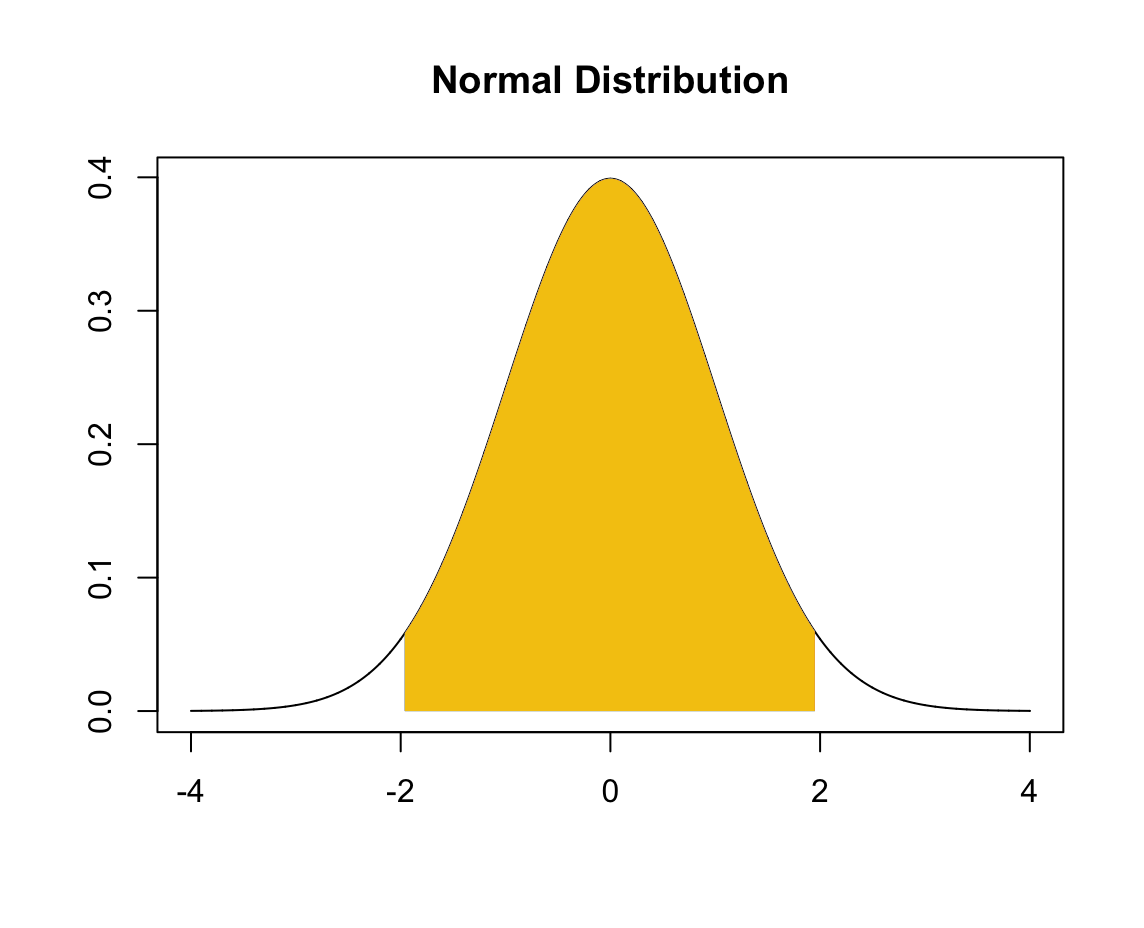
[R] 위 그림 코드
x<-seq(-4,4,0.001)
y<-dnorm(x)
plot(x,y,type="l",ann=FALSE)
title(main="Normal Distribution")
xrange<-seq(-1.959964,1.959964,0.01)
funx<-dnorm(xrange)
polyx<-c(xrange,rev(xrange))
polyy<-c(rep(0,length(funx)),rev(funx))
polygon(polyx,polyy,col=7,border=NA)
카이 제곱은 정규분포를 제곱한다고 하였다.
0은 0으로,
1은 1로,
2는 4로,
3은 9로,
4는 16으로 이동한다.
음의 영역에서도
-1은 1로,
-2는 4로,
-3은 9로,
-4는 16으로 이동한다.
즉 $x=0$이라는 직선을 기준으로 그래프를 반으로 접은 뒤에 양옆으로 잡아당긴 형태가 된다.
따라서 카이 제곱 분포의 그래프는 음의 영역이 존재하지 않는다.
그러면 위 그림의 노란색 영역은 어떻게 변할까?
1.96의 제곱도 3.84, -1.96의 제곱도 3.84이다.
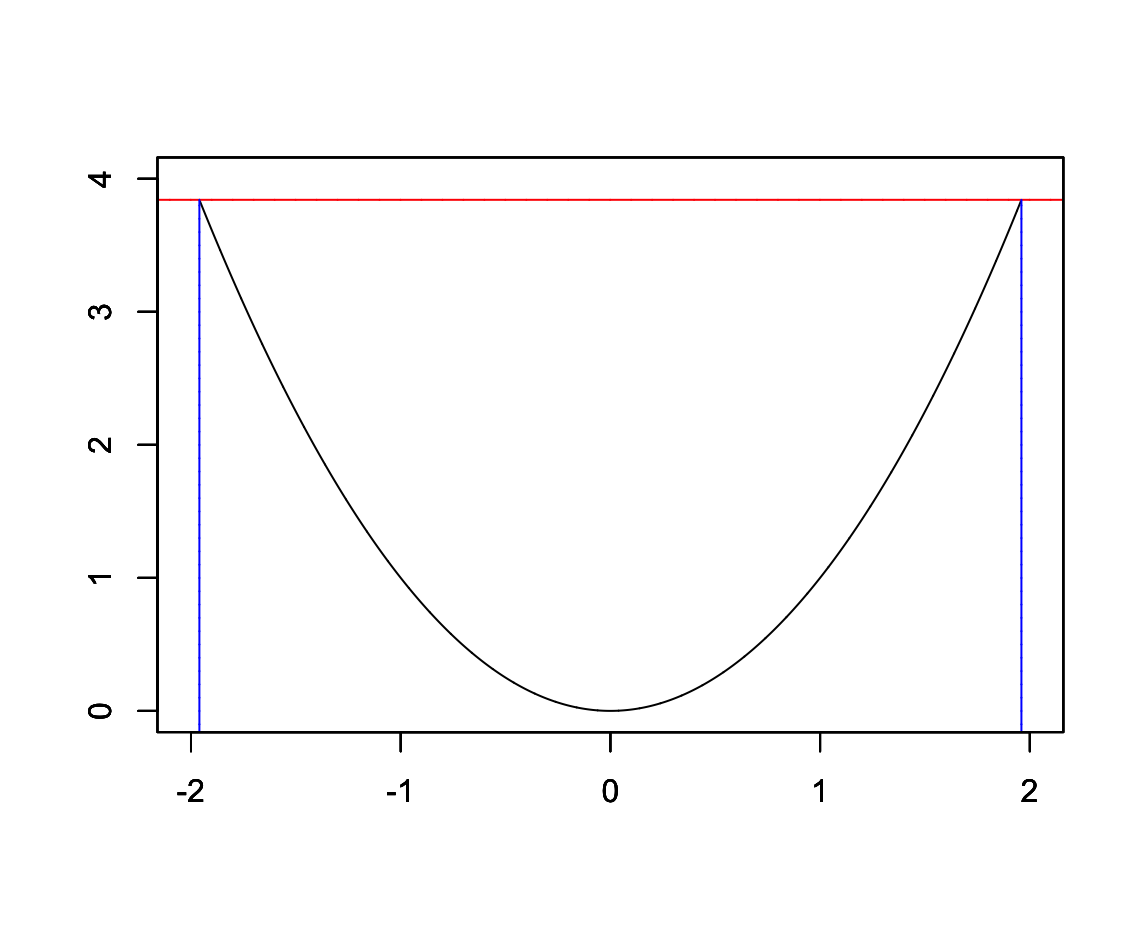
[R] 위 그림 코드
x<-seq(-1.959964,1.959964,0.001)
y<-x^2
plot(x,y,type="l",ann=FALSE,xlim=c(-2,2),ylim=c(0,4))
par(new=TRUE)
x<-seq(-3,3,0.001)
y<-x*0+3.841458821
plot(x,y,type="l",col="red",ann=FALSE,xlim=c(-2,2),ylim=c(0,4))
par(new=TRUE)
y<-seq(-3,3.841458821,0.001)
x<-y*0-1.959964
plot(x,y,type="l",col="blue",ann=FALSE,xlim=c(-2,2),ylim=c(0,4))
par(new=TRUE)
y<-seq(-3,3.841458821,0.001)
x<-y*0+1.959964
plot(x,y,type="l",col="blue",ann=FALSE,xlim=c(-2,2),ylim=c(0,4))
따라서, 0에서 3.84까지 적분한 값이 0.95가 되는 아래와 같은 그래프일 것이다.
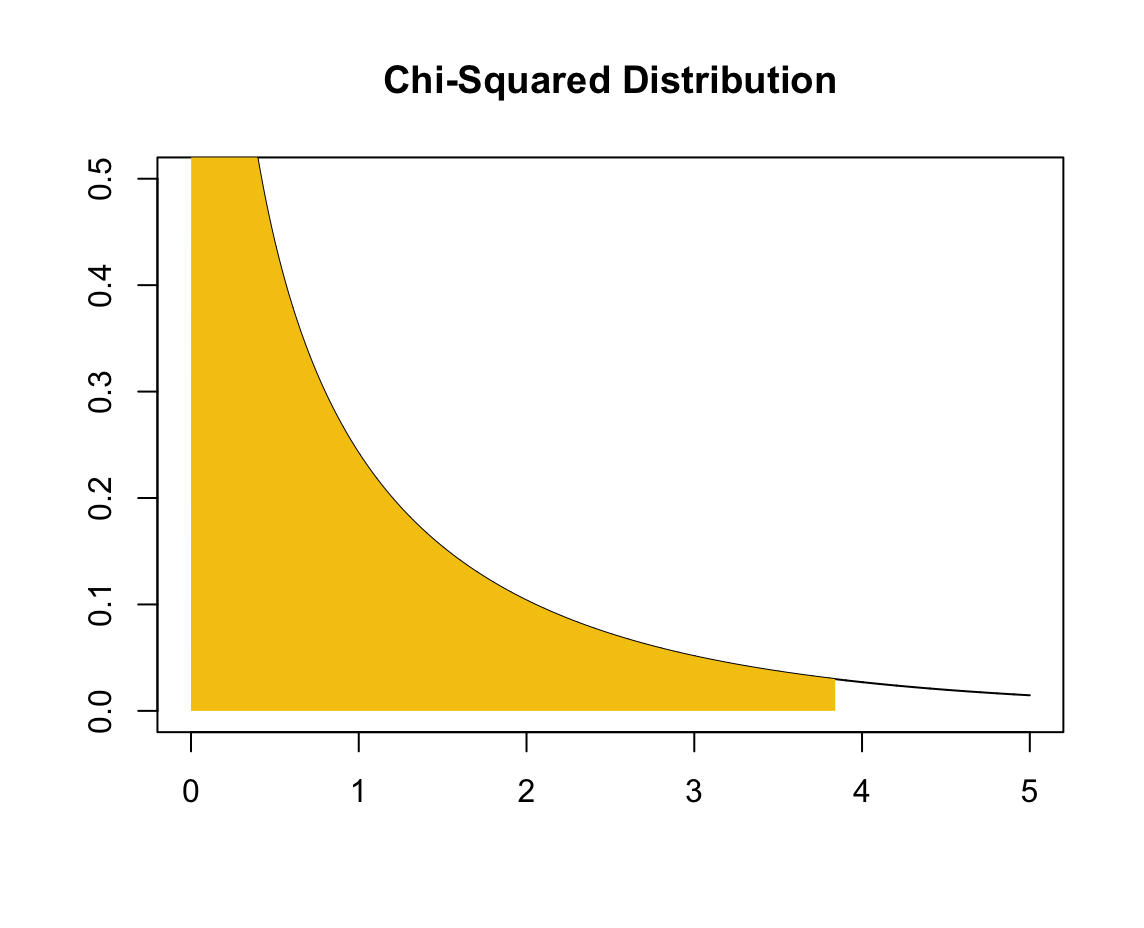
[R] 위 그림 코드
x<-seq(0,5,0.001)
y<-dchisq(x,1)
plot(x,y,type="l",ann=FALSE, ylim=c(0,0.5))
title(main="Chi-Squared Distribution")
xrange<-seq(0,3.841458821,0.01)
funx<-dchisq(xrange,1)
polyx<-c(xrange,rev(xrange))
polyy<-c(rep(0,length(funx)),rev(funx))
polygon(polyx,polyy,col=7,border=NA)
따라서, 일반적인 양수에 대해 다음의 두 등식이 성립한다.
[1] pnorm(a)=0.5*pchisq(a^2,1)+0.5
[2] pnorm(-a)+0.5*pchisq(a^2,1)+0.5=1
그런데 자유도는 왜 존재하는 개념인가?
| 흡연자 | 비흡연자 | 총합 | |
| 폐암 환자 | (A) | (B) | 200 |
| 정상인 | (C) | (D) | 800 |
| 총합 | 300 | 700 | 1000 |
우리는 위에서 폐암 환자는 200명, 정상인은 800명, 흡연자는 300명, 비흡연자는 700명이라는 사실이 변하지 않는다고 가정하고 논의를 이어갔다. 여기에서 만약 (A)가 100이라면 (B), (C), (D)의 값은 바로 100, 200, 600으로 정해진다. 우리가 "자유"로이 정할 수 있는 값은 (A), (B), (C), (D)중 단 한 개일 뿐이다. 따라서 자유도는 1이 된다.
자유도를 구하는 공식은 왜 $\left(열의\ 개수 - 1 \right)\times\left(행의\ 개수 - 1 \right)$인가?
| 저체중 | 정상 | 비만 | 총합 | |
| 초등학교 졸업 | (A) | (B) | (C) | |
| 중학교 졸업 | (D) | (E) | (F) | |
| 고등학교 졸업 | (G) | (H) | (I) | |
| 대학교 졸업 이상 | (J) | (K) | (L) | |
| 총합 |
각 영역의 총합은 정해져 있으므로 "초등학교 졸업"영역에서 자유로이 정할 수 있는 것은 (A), (B), (C)중 두 개 뿐이다. 두 개의 값을 정하면 나머지 하나는 자연스럽게 정해지기 때문이다. 여기에서는 (A), (B)를 자유롭게 정했다고 하자.
저체중 영역에서도 (A), (D), (G), (J) 중 세 개만 자유롭게 정할 수 있는데 (A), (D), (G)를 자유로이 정했다고 하자. 같은 방식으로 논리를 전개하면 자유롭게 정할 수 있는 값은 파란 색으로 표시된 6개 뿐이다. 즉, 열의 개수에서 1을 뺀 값과, 행의 개수에서 1을 뺀 값을 곱하여 자유도를 구할 수 있게 된다.
[이론] 카이 제곱 검정 (Chi-squared test) 정복 완료!
작성일: 2022.08.16.
최종 수정일: 2022.08.16.
이용 프로그램: R 4.1.3
RStudio v1.4.1717
RStudio 2021.09.1+372 "Ghost Orchid" Release
운영체제: Windows 10, Mac OS 10.15.7
'통계 이론' 카테고리의 다른 글
| [이론] p-value에 관한 고찰 (0) | 2022.09.05 |
|---|---|
| [이론] 연속성을 수정한 카이 제곱 검정 (Chi-squared test with Yates's correction for continuity) (0) | 2022.08.30 |
| [이론] 카이 제곱 검정과 피셔 정확 검정의 관계 (0) | 2022.08.29 |
| [이론] 피셔 정확 검정 (Fisher's exact test) (0) | 2022.08.26 |
| [이론] Q-Q Plot (Quantile-Quantile Plot) (0) | 2022.08.12 |