[R] 윌콕슨 부호 순위 검정 (비모수 짝지어진 표본 중앙값 검정: Wilcoxon signed rank test) - wilcox.test()
짝지어진 두 분포의 평균이 다른지 확인하는 방법을 이전에는 대응 표본 T검정 (Paireed Sample T test)로 시행했었다. (2022.11.25 - [반복 측정 자료 분석/R] - [R] 대응 표본 T검정 (Paired samples T-test) - t.test()) 하지만 여기에는 중요한 가정이 필요한데, 두 변수의 차이가 정규분포를 이룬다는 것이다. 하지만 차이의 분포가 정규성을 따르지 않는다면 어떻게 해야 할까? 그럴 때 사용하는 것이 Wilcoxon signed rank test (윌콕슨 부호 순위 검정)이다.
*실습용 데이터는 아래 링크를 클릭하면 다운로드할 수 있습니다.
2022.08.04 - [공지사항 및 소개] - 분석용 데이터 (update 22.12.01)
분석용 데이터 (update 22.12.01)
2022년 12월 01일 버전입니다. 변수는 계속하여 추가될 예정입니다. 다음 카테고리에 있는 글에서 이용된 데이터입니다. - 기술 통계 - 범주형 자료 분석 - 모평균 검정 - 반복 측정 자료 분석 - 통계
medistat.tistory.com
코드를 보여드리기에 앞서 워킹 디렉토리부터 지정하겠다.
워킹 디렉토리에 관한 설명은 다음 링크된 포스트에서 볼 수 있다.
2022.08.05 - [통계 프로그램 사용 방법/R] - [R] 작업 디렉토리 (Working Directory) 지정 - getwd(), setwd()
setwd("C:/Users/user/Documents/Tistory_blog")
데이터를 불러와 df에 객체로 저장하겠다.
데이터 불러오는 방법은 다음 링크에서 볼 수 있다.
2022.08.05 - [통계 프로그램 사용 방법/R] - [R] 데이터 불러오기 : EXCEL - read_excel(), read.xlsx()
2022.08.10 - [통계 프로그램 사용 방법/R] - [R] 데이터 저장하기 : CSV 파일 - write.csv(), write_csv()
2022.08.10 - [통계 프로그램 사용 방법/R] - [R] 데이터 불러오기 : SAS file (.sas7bdat) - read.sas7bdat(), read_sas()
install.packages("readr")
library("readr")
df<-read_csv("Data.csv")
목표: 모집단에서 GGT와 간기능 개선제 복용 후 GGT 중앙값에 차이가 있다고 할 수 있는가?
이번 포스팅의 목적은 1000명의 데이터를 가지고, 이 1000명이 기원한 모집단에서 GGT와 간 기능 개선제 복용 후 GGT의 중앙값에 차이가 있다고 할 수 있는지 판단하는 것이다.
전제: 정규성 검정 (차이)
검정하고자 하는 두 변수의 차이가 정규성을 띤다면 paired t-test를 하면 되므로 정규성 여부를 파악하도록 한다. 따라서 GGT와 간 기능 개선제 복용 후 GGT(GGT_POSTMED)의 차이를 구하고 정규성 검정을 시행한다.
차이를 구하는 방법:
2022.11.25 - [통계 프로그램 사용 방법/R] - [R] 변수 계산 (산술 연산)
정규성 검정을 하는 방법:
2022.08.11 - [기술 통계/R] - [R] 정규성 검정 (1) : Q-Q plot - qqnorm(), qqline()
2022.08.11 - [기술 통계/R] - [R] 정규성 검정 (2) : 히스토그램 - hist(), dnorm()
2022.08.12 - [기술 통계/R] - [R] 정규성 검정 (4) : 정량적 검정 (Lilliefors test) - lillie.test()
2022.08.16 - [기술 통계/R] - [R] 고급 Q-Q Plot - Van der Waerden, Rankit, Tukey, Blom
코드
##GGT 차이 변수 만들기
df$GGT_DIF<-df$GGT-df$GGT_POSTMED
##GGT_DIF의 정규성 검정
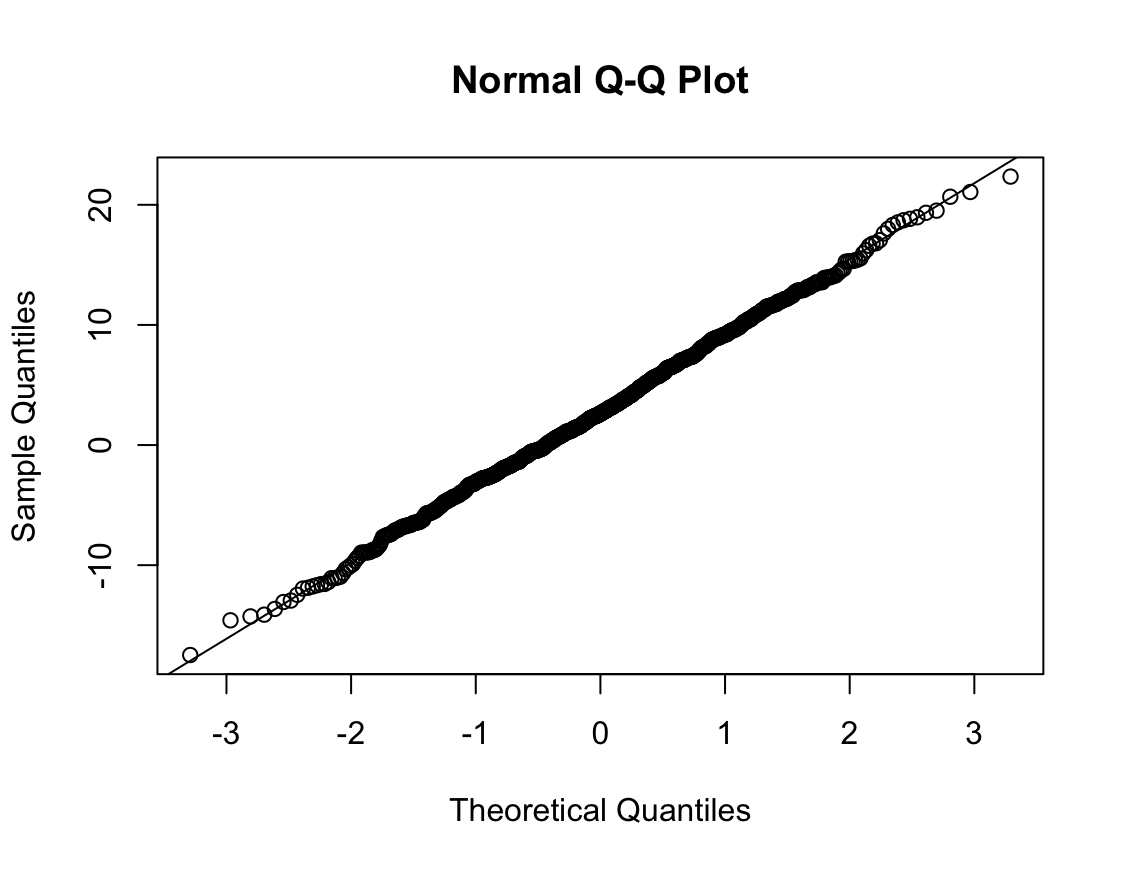
# 1) Q-Q plot 그리기
qqnorm(df$GGT_DIF)
qqline(df$GGT_DIF)
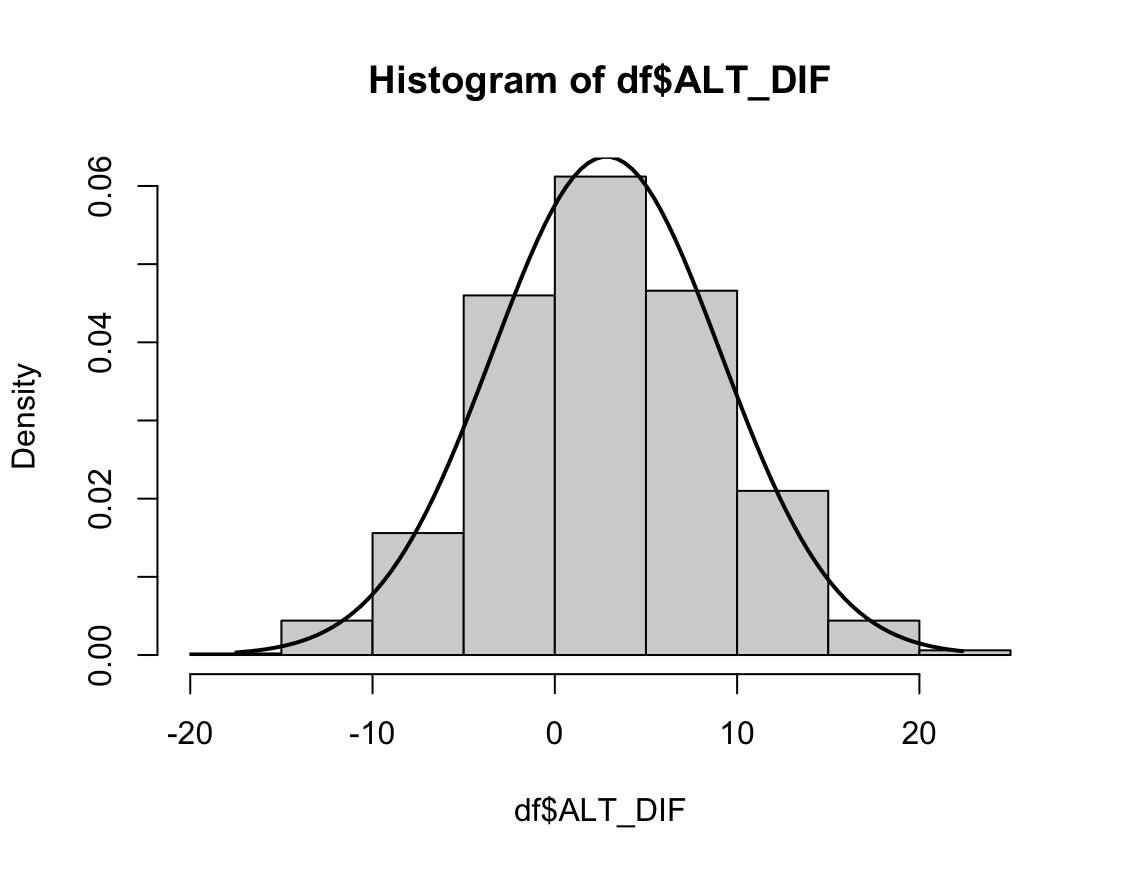
# 2) 히스토그램 그리기
hist(df$GGT_DIF, prob=TRUE, breaks=20)
GGT_DIFrange<-seq(min(df$GGT_DIF),max(df$GGT_DIF),length=max(max(df$GGT_DIF)-min(df$GGT_DIF),100))
ND<-dnorm(GGT_DIFrange,mean=mean(df$GGT_DIF),sd=sd(df$GGT_DIF))
lines(GGT_DIFrange, ND, lwd=2)
# 3) Shapiro-Wilk test 시행하기
shapiro.test(df$GGT_DIF)
결과


Shapiro-Wilk normality test
data: df$GGT_DIF
W = 0.94868, p-value < 2.2e-16N수가 2,000개 미만이므로 Shapiro-Wilk 통계량의 p-value를 보면 0.05 이하이며, Q-Q Plot은 대부분의 데이터가 선상에 있지 않다. 히스토그램에서는 정규성을 따르는 것처럼 보이지만 이는 개인의 느낌이므로 정확한 것은 아니다. 따라서 대응 표본 T검정 (Paired sample T-test)를 시행할 수 없고, 윌콕슨 부호 순위 검정 (Wilcoxon Signed Rank Test)을 시행해야 한다.
윌콕슨 부호 순위 검정 (Wilcoxon Signed Rank Test) 코드
wilcox.test(df$GGT, df$GGT_POSTMED, correct=FALSE, paired=TRUE)wilcox.test(df$GGT, df$GGT_POSTMED, correct=FALSE, paired=TRUE) : df데이터의 GGT변수와 df데이터의 GGT_POSTMED로 검정을 하는데, 연속성 수정은 하지 말고 (correct=FALSE), 대응표본이니까 (paired=TRUE) 윌콕슨 부호 순위 검정을 시행하라. (연속성 수정은 다음 글을 참고하길 바란다.2022.08.30 - [통계 이론] - [이론] 연속성을 수정한 카이 제곱 검정 (Chi-squared test with Yates's correction for continuity))
결과
Wilcoxon signed rank test
data: df$GGT and df$GGT_POSTMED
V = 22907, p-value < 2.2e-16
alternative hypothesis: true location shift is not equal to 0Wilcoxon signed rank test
data: df$GGT and df$GGT_POSTMED
V = 22907, p-value < 2.2e-16
alternative hypothesis: true location shift is not equal to 0
중요한 건 p-value다. p-value가 0.05보다 작으므로 df의 GGT와 GGT_POSTMED는 차이가 있다고 할 수 있다. 지난번 일표본 윌콕슨 부호 순위 검정에서도 밝혔듯이 윌콕슨 부호 순위 검정은 가정이 필요 없는 검정이 아니다. 대칭이라는 가정이 필요하다.(2022.11.29 - [모평균 검정/R] - [R] 일표본 윌콕슨 부호 순위 검정 (비모수 일표본 중앙값 검정: One-Sample Wilcoxon Signed Rank Test) - wilcox.test()) 따라서 대칭여부를 확인해야 하는데, 위 GGT_DIF의 히스토그램을 보면 좌우대칭임을 확인할 수 있다. 따라서 원 결론 그대로 차이가 난다고 결론을 내리면 된다.
그런데, 눈치를 챈 독자도 있겠지만, 비모수 일표본 검정도, 대응 표본 검정도 모두 윌콕슨 부호 순위 검정을 실시한다. 이는 모수적인 방법에서 대응 표본 T 검정 (paired T test)가 사실 일표본 T 검정 (One sample T test)와 같다는 것과 일맥상통하는 이야기다. 이 말을 비틀어 생각하면, 일표본 윌콕슨 부호 순위 검정으로 대응표본 윌콕슨 부호 순위 검정을 시행할 수 있다는 말이다. 즉 위에서 만들 DDT_DIF변수로 0에 대해 일표본 윌콕슨 부호 순위 검정을 시행하면 같은 결과를 내는 것을 확인할 수 있다.
코드
wilcox.test(df$GGT_DIF, mu=0, correct=FALSE)
결과
Wilcoxon signed rank test
data: df$GGT_DIF
V = 22907, p-value < 2.2e-16
alternative hypothesis: true location is not equal to 0
코드 정리
##워킹 디렉토리 지정
setwd("C:/Users/user/Documents/Tistory_blog")
##데이터 불러오기
install.packages("readr")
library("readr")
df<-read_csv("Data.csv")
##GGT 차이 변수 만들기
df$GGT_DIF<-df$GGT-df$GGT_POSTMED
##GGT_DIF의 정규성 검정
# 1) Q-Q plot 그리기
qqnorm(df$GGT_DIF)
qqline(df$GGT_DIF)
# 2) 히스토그램 그리기
hist(df$GGT_DIF, prob=TRUE, breaks=20)
GGT_DIFrange<-seq(min(df$GGT_DIF),max(df$GGT_DIF),length=max(max(df$GGT_DIF)-min(df$GGT_DIF),100))
ND<-dnorm(GGT_DIFrange,mean=mean(df$GGT_DIF),sd=sd(df$GGT_DIF))
lines(GGT_DIFrange, ND, lwd=2)
# 3) Shapiro-Wilk test 시행하기
shapiro.test(df$GGT_DIF)
##윌콕슨 부호 순위 검정 시행하기
wilcox.test(df$GGT, df$GGT_POSTMED, correct=FALSE, paired=TRUE)
##일표본 윌콕슨 부호 순위 검정 시행하기
wilcox.test(df$GGT_DIF, mu=0, correct=FALSE)
[R] 윌콕슨 부호 순위 검정 (비모수 짝지어진 표본 중앙값 검정: Wilcoxon signed rank test) 정복 완료!
작성일: 2022.12.01.
최종 수정일: 2022.12.06.
이용 프로그램: R 4.2.2
RStudio v2022.07.2
RStudio 2022.07.2+576 "Spotted Wakerobin" Release
운영체제: Windows 10, Mac OS 12.6.1
'반복 측정 자료 분석 > R' 카테고리의 다른 글
| [R] 대응 표본 T검정 (Paired samples T-test) - t.test() (0) | 2022.11.25 |
|---|