
[R] 독립 표본 T검정 (Independent samples T-test) - t.test(), var.test(), levene.test()
세상에 존재하는 모든 사람을 대상으로 연구를 하면 참 좋겠지만, 시간적인 이유로, 그리고 경제적인 이유로 일부를 뽑아서 연구를 진행할 수밖에 없다. 모든 사람을 모집단이라고 하고, 뽑힌 일부를 표본이라고 한다. 우리는 표본으로 시행한 연구로 모집단에 대한 결론을 도출해내고자 할 것이다.
1000명에게 피검사를 시행하였고, 간 기능 검사의 일환으로 ALT 수치를 모았다. 이 데이터를 기반으로 1000명이 기원한 모집단 인구에서의 ALT평균이 어떻게 될지 예측하는 것이 T-test이다. T-test는 크게 세 가지로 나눌 수 있다.
1) 일표본 T검정 (One sample T-test) : 2022.11.03 - [모평균 검정/R] - [R] 일표본 T검정 (One-sample T-test) - t.test()
: 모집단의 평균이 특정 값이라고 할 수 있는가?
예) 모집단의 ALT 평균이 50이라고 할 수 있는가?
2) 독립 표본 T검정 (Independent samples T-test, Two samples T-test)
: 두 모집단의 평균이 다르다고 할 수 있는가?
예) 고혈압 환자와 일반인의 수축기 혈압 평균이 서로 다르다고 할 수 있는가?
3) 대응표본 T검정 (Paired samples T-test) : 2022.11.25 - [반복 측정 자료 분석/R] - [R] 대응 표본 T검정 (Paired samples T-test) - t.test()
: 모집단의 짝지어진 변수들의 평균이 다르다고 할 수 있는가?
예) 간기능 개선제 복용 전 ALT 평균은 간기는 개선제 복용 후 ALT 평균과 다르다고 할 수 있는가?
이번 포스팅에서는 독립 표본 T검정 (Independent samples T-test, Two samples T-test)에 대해 알아볼 것이다.
*실습용 데이터는 아래 링크를 클릭하면 다운로드할 수 있습니다.
2022.08.04 - [공지사항 및 소개] - 분석용 데이터 (update 22.10.11)
분석용 데이터 (update 22.10.11)
2022년 10월 11일 버전입니다. 변수는 계속하여 추가될 예정입니다. 다음 카테고리에 있는 글에서 이용된 데이터입니다. - 기술 통계 - 범주형 자료 분석 - 모평균 검정 - 반복 측정 자료 분석 - 통계
medistat.tistory.com
코드를 보여드리기에 앞서 워킹 디렉토리부터 지정하겠다.
워킹 디렉토리에 관한 설명은 다음 링크된 포스트에서 볼 수 있다.
2022.08.05 - [통계 프로그램 사용 방법/R] - [R] 작업 디렉토리 (Working Directory) 지정 - getwd(), setwd()
setwd("C:/Users/user/Documents/Tistory_blog")
데이터를 불러와 df에 객체로 저장하겠다.
데이터 불러오는 방법은 다음 링크에서 볼 수 있다.
2022.08.05 - [통계 프로그램 사용 방법/R] - [R] 데이터 불러오기 : EXCEL - read_excel(), read.xlsx()
2022.08.10 - [통계 프로그램 사용 방법/R] - [R] 데이터 저장하기 : CSV 파일 - write.csv(), write_csv()
2022.08.10 - [통계 프로그램 사용 방법/R] - [R] 데이터 불러오기 : SAS file (.sas7bdat) - read.sas7bdat(), read_sas()
install.packages("readr")
library("readr")
df<-read_csv("Data.csv")
목표: 고혈압 환자의 수축기 혈압(SBP) 평균은 정상인의 수축기 혈압 평균과 다르다고 모집단 수준에서 말할 수 있는가?
이번 포스팅의 목적은 1000명의 데이터를 가지고, 이 1000명이 기원한 모집단에서 수축기 혈압 평균이 고혈압 유병 여부에 따라 다르다고 할 수 있는지 판단하는 것이다.
전제조건 (정규성) - 코드
독립 표본 (Indepent samples, Two tamples) T 검정의 전제조건은 각각의 독립 표본의 분포가 정규성을 따른다는 것이다. 즉, 여기에서는 고혈압 유병 여부에 따라 수축기 혈압 (SBP)의 정규성을 검정하도록 하겠다.
따라서 다음 두 가지의 일을 해야 한다.
1) 고혈압 여부에 따라 데이터를 나누기
나누는 방법에 대한 설명은 다음 링크에서 볼 수 있다. 2022.11.10 - [통계 프로그램 사용 방법/R] - [R] 조건에 맞는 자료 추출하기
위 링크에서 확인할 수 있듯이 여러 가지 방법으로 나눌 수 있지만 indexing을 이용하여 나누도록 하겠다.
df_whtn<-df[df$HTN==1,]
df_wohtn<-df[df$HTN==0,]
2) 고혈압 여부에 따라 정규성을 검정하기
정규성 검정에 대한 설명은 다음 링크들에서 확인할 수 있다.
2022.08.11 - [기술 통계/R] - [R] 정규성 검정 (1) : Q-Q plot - qqnorm(), qqline()
2022.08.11 - [기술 통계/R] - [R] 정규성 검정 (2) : 히스토그램 - hist(), dnorm()
2022.08.12 - [기술 통계/R] - [R] 정규성 검정 (4) : 정량적 검정 (Lilliefors test) - lillie.test()
2022.08.16 - [기술 통계/R] - [R] 고급 Q-Q Plot - Van der Waerden, Rankit, Tukey, Blom
##고혈압 환자의 수축기 혈압 정규성 검정
# 1) Q-Q plot 그리기
qqnorm(df_whtn$SBP)
qqline(df_whtn$SBP)
# 2) 히스토그램 그리기
hist(df_whtn$SBP, prob=TRUE)
SBPrange<-seq(min(df_whtn$SBP),max(df_whtn$SBP),length=max(max(df_whtn$SBP)-min(df_whtn$SBP),100))
ND<-dnorm(SBPrange,mean=mean(df_whtn$SBP),sd=sd(df_whtn$SBP))
lines(SBPrange, ND, lwd=2)
# 3) Shapiro-Wilk test 시행하기
shapiro.test(df_whtn$SBP)
##정상인의 수축기 혈압 정규성 검정
# 1) Q-Q plot 그리기
qqnorm(df_wohtn$SBP)
qqline(df_wohtn$SBP)
# 2) 히스토그램 그리기
hist(df_wohtn$SBP, prob=TRUE)
SBPrange<-seq(min(df_wohtn$SBP),max(df_wohtn$SBP),length=max(max(df_wohtn$SBP)-min(df_wohtn$SBP),100))
ND<-dnorm(SBPrange,mean=mean(df_wohtn$SBP),sd=sd(df_wohtn$SBP))
lines(SBPrange, ND, lwd=2)
# 3) Shapiro-Wilk test 시행하기
shapiro.test(df_wohtn$SBP)
정규성 검정 - 결과
1) 고혈압 환자
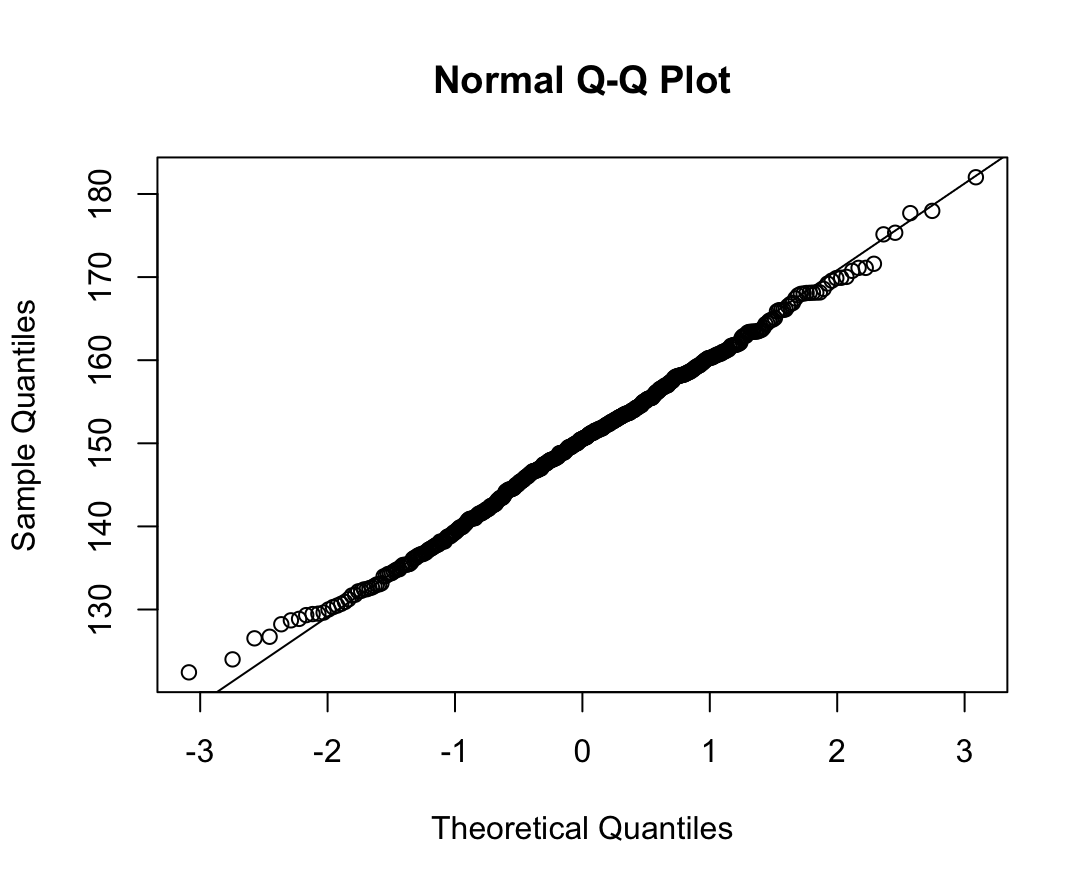
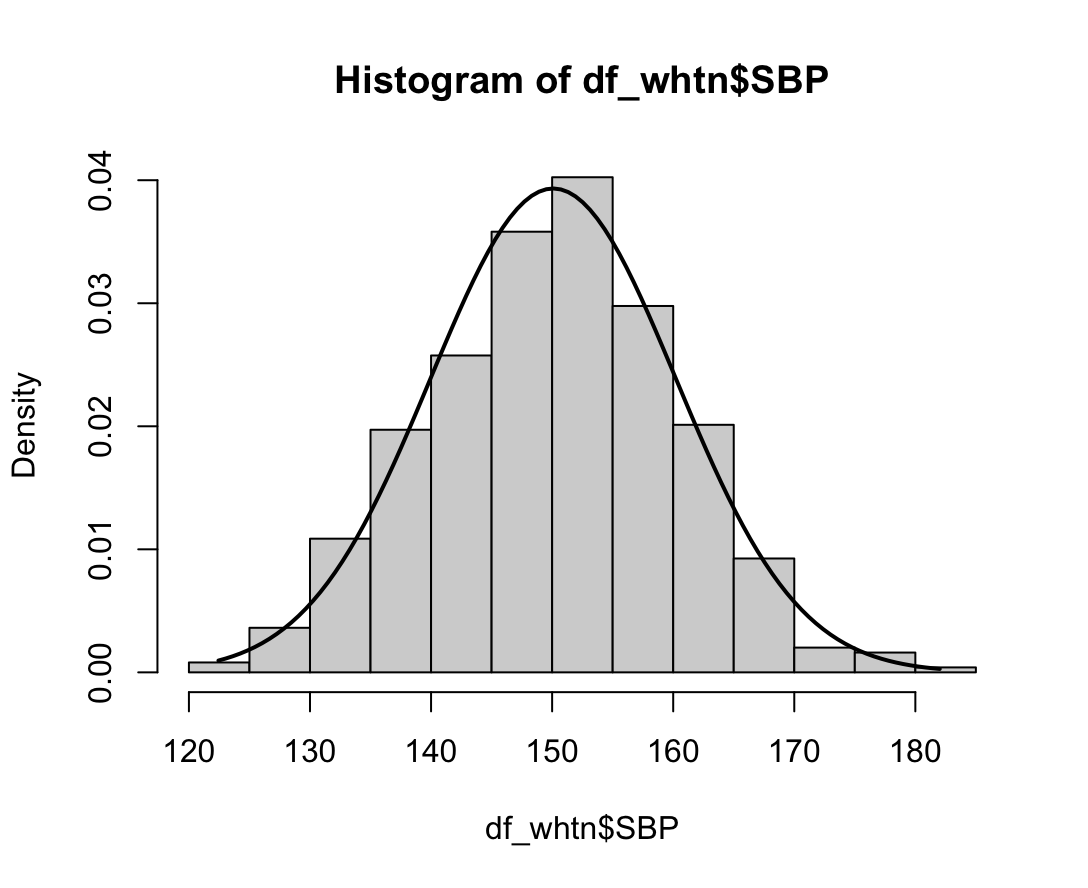
Shapiro-Wilk normality test
data: df_whtn$SBP
W = 0.9975, p-value = 0.6677N수가 2,000개 미만이므로 Shapiro-Wilk 통계량의 p-value를 보면 0.05 이상이며, Q-Q Plot은 대부분의 데이터가 선상에 있고, 히스토그램에서도 정규성을 따르는 것처럼 볼 수 있다.
2) 정상인
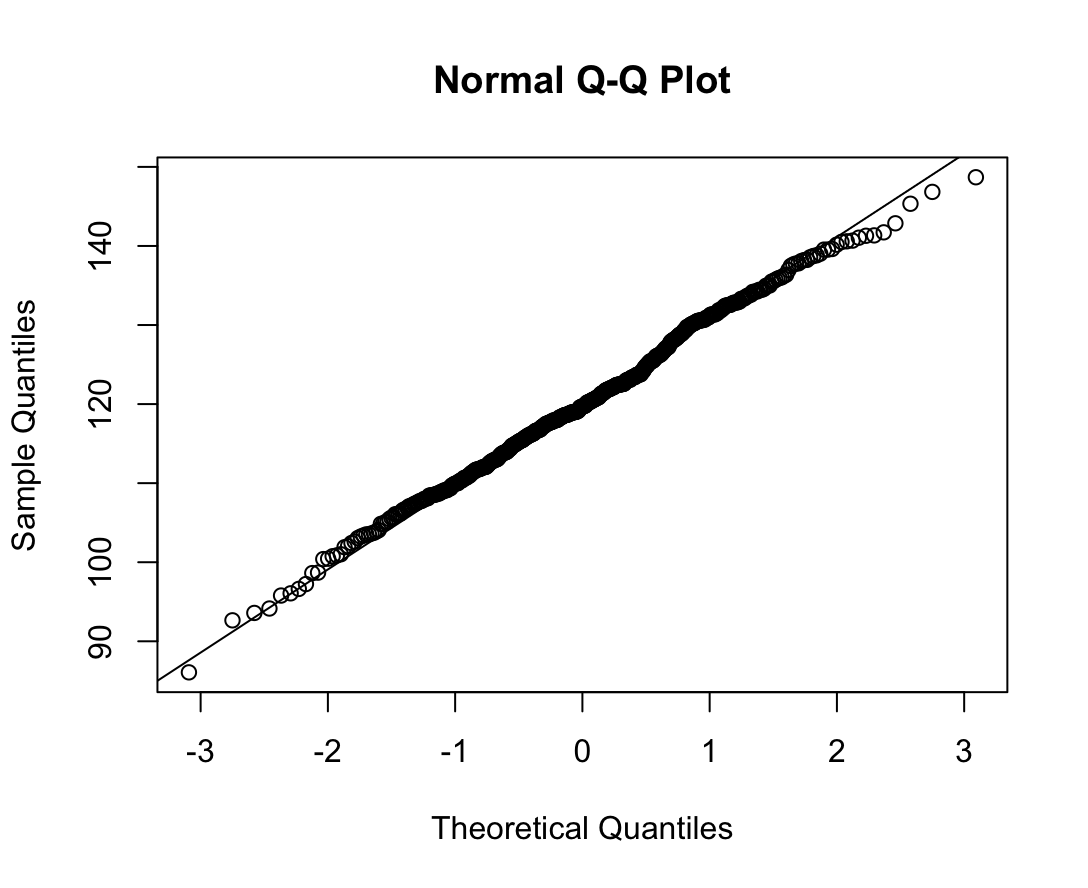
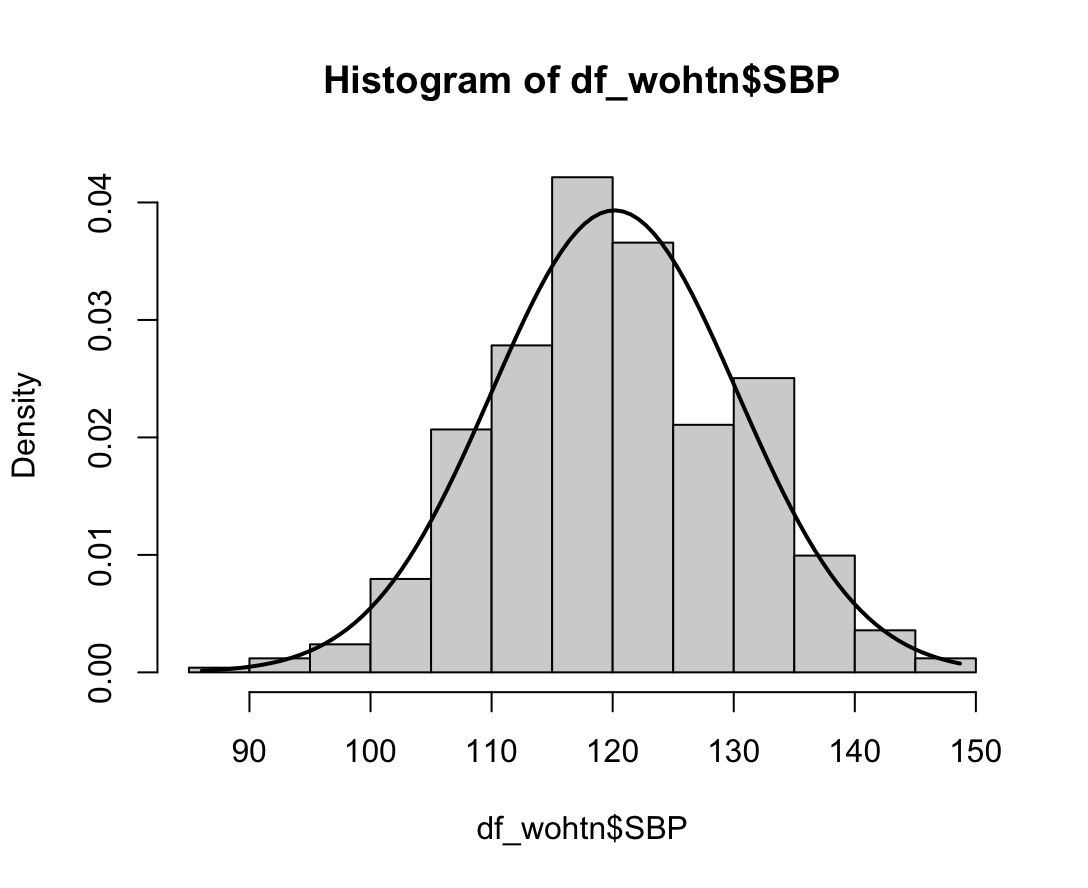
Shapiro-Wilk normality test
data: df_wohtn$SBP
W = 0.99676, p-value = 0.4119N수가 2,000개 미만이므로 Shapiro-Wilk 통계량의 p-value를 보면 0.05 이상이며, Q-Q Plot은 대부분의 데이터가 선상에 있고, 히스토그램에서도 정규성을 따르는 것처럼 볼 수 있다.
전제조건이 성립한다. 즉, 고혈압 유병 여부에 따른 수축기 혈압 (SBP)의 분포가 정규성을 따른다고 할 수 있다. 따라서 독립 표본 T 검정 (Independent samples T test, Two samples T test)을 시행할 수 있다.
등분산성 검정
독립 표본 T 검정 (Independent samples T test, Two samples T test)은 고혈압 유병 여부에 따른 수축기 혈압의 분포의 분산이 같은지 여부에 따라 시행하는 검사 방법이 다르다. 따라서 분산이 같은지 확인하는 등분산성 검정을 먼저 시행해야 한다.
많이 사용하는 등분산성 검정 방법은 다음 다섯 가지가 있다.
1) F test
2) Levene의 등분산 검정
3) O'Brien의 등분산 검정(R에서 검정 불가)
4) Brown and Forsythe의 등분산 검정
5) Bartlett의 등분산 검정
이 글에서는 F test와 Levene의 등분산 검정까지만 해보고, 나머지는 다음 링크에서 다루기로 한다. 2022.11.20 - [모평균 검정/R] - [R] 등분산성 검정 (Homogeneity of variance) - levene.test(), bartlett.test()
#F test
var.test(SBP~HTN, data=df)
#Levene의 등분산 검정
install.packages("lawstat")
library("lawstat")
levene.test(df$SBP, df$HTN, location="mean")#F test
var.test(SBP~HTN, data=df) : 등분산 검정을 하는데, HTN에 따라 SBP의 분포의 분산이 같은지 검정하라. 데이터는 df를 사용한다.
#Levene의 등분산 검정
install.packages("lawstat") : Levene의 등분산 검정을 하기 위해서는 lawstat이라는 패키지를 설치해야 한다.
library("lawstat") : lawstat패키지를 불러온다.
levene.test(df$SBP, df$HTN, location="mean") : df 데이터의 HTN에 따라 df 데이터의 SBP의 분포의 분산이 같은지 검정하라. 이때 [location="mean"]을 적어주어야 Levene의 등분산 검정을 시행한다.
결과
F test to compare two variances
data: SBP by HTN
F = 0.99995, num df = 502, denom df = 496, p-value =
0.9994
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.8387988 1.1919414
sample estimates:
ratio of variances
0.9999465
Classical Levene's test based on the absolute deviations
from the mean ( none not applied because the location is
not set to median )
data: df$SBP
Test Statistic = 0.010363, p-value = 0.9189 F test to compare two variances
data: SBP by HTN
F = 0.99995, num df = 502, denom df = 496, p-value =0.9994
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.8387988 1.1919414
sample estimates:
ratio of variances
0.9999465
Classical Levene's test based on the absolute deviations from the mean ( none not applied because the location is not set to median )
data: df$SBP
Test Statistic = 0.010363, p-value = 0.9189
결과 창에 나오는 것들이 많아 복잡해 보이지만 위에 파란색 볼드로 처리해놓은 내용만 보면 된다. F test의 p-value는 0.9994, Levene의 등분산 검정의 p-value는 0.9189이다. 모두 0.05보다 크므로 귀무가설을 기각할 수 없으며 귀무가설을 택해야 한다. 여기에서의 귀무가설은 "HTN에 따라 SBP의 분포의 분산에 차이가 없다."이므로 분산이 같다는 결론을 내린다.
이제 드디어 사전 점검이 모두 끝났고, t-test를 시행할 수 있다.
코드
##T-test
t.test(df_wohtn$SBP, df_whtn$SBP, var.equal=TRUE)
t.test(df_wohtn$SBP, df_whtn$SBP, var.equal=TRUE) : 고혈압이 없는 사람들의 수축기 혈압 (df_wohtn$SBP)과 고혈압이 있는 사람들의 수축기 혈압 (df_whtn$SBP)으로 t-test를 시행하라. 대신 두 군의 분산은 같다고 가정한다.
만약, 등분산성 검정 결과 분산이 다르다고 결론이 났으면 "var.equal=FALSE" 라고 적으면 된다. 혹은 t.test의 var.equal은 FALSE를 기본값으로 가지므로, "var.equal=TRUE"를 그냥 지워도 된다.
결과
Two Sample t-test
data: df_wohtn$SBP and df_whtn$SBP
t = -46.666, df = 998, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-31.19793 -28.68000
sample estimates:
mean of x mean of y
120.1473 150.0862Two Sample t-test
data: df_wohtn$SBP and df_whtn$SBP
t = -46.666, df = 998, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval: -31.19793 -28.68000
sample estimates:
mean of x mean of y
120.1473 150.0862
결과가 복잡한 듯 하지만 파란색 글씨만 읽으면 된다. p-value는 $2.2 \times 10^{-16}$보다 작다. 따라서 귀무가설을 기각할 수 있으며, 본 검정에서 귀무가설은 "HTN에 따라 SBP의 평균이 같다."이므로 "HTN에 따라 SBP의 평균은 다르다."라고 결론 내릴 수 있다. 마지막 행을 보면 "mean of x"은 120.1473, "mean of y"은 150.0862라고 알려주고 있는데, x는 코드에 처음 들어간 "df_wohtn$SBP"를 의미하고, y는 두 번째로 들어간 "df_whtn$SBP"를 의미한다. 즉 고혈압이 없는 군의 수축기 혈압 평균은 120.1473, 고혈압이 없는 군의 수축기 혈압 평균은 150.0862다.
코드 정리
#워킹 디렉토리 지정
setwd("C:/Users/user/Documents/Tistory_blog")
#파일 불러오기
install.packages("readr")
library("readr")
df<-read_csv("Data.csv")
#고혈압 여부에 따라 데이터 나누기
df_whtn<-df[df$HTN==1,]
df_wohtn<-df[df$HTN==0,]
##고혈압 환자의 수축기 혈압 정규성 검정
# 1) Q-Q plot 그리기
qqnorm(df_whtn$SBP)
qqline(df_whtn$SBP)
# 2) 히스토그램 그리기
hist(df_whtn$SBP, prob=TRUE)
SBPrange<-seq(min(df_whtn$SBP),max(df_whtn$SBP),length=max(max(df_whtn$SBP)-min(df_whtn$SBP),100))
ND<-dnorm(SBPrange,mean=mean(df_whtn$SBP),sd=sd(df_whtn$SBP))
lines(SBPrange, ND, lwd=2)
# 3) Shapiro-Wilk test 시행하기
shapiro.test(df_whtn$SBP)
##정상인의 수축기 혈압 정규성 검정
# 1) Q-Q plot 그리기
qqnorm(df_wohtn$SBP)
qqline(df_wohtn$SBP)
# 2) 히스토그램 그리기
hist(df_wohtn$SBP, prob=TRUE)
SBPrange<-seq(min(df_wohtn$SBP),max(df_wohtn$SBP),length=max(max(df_wohtn$SBP)-min(df_wohtn$SBP),100))
ND<-dnorm(SBPrange,mean=mean(df_wohtn$SBP),sd=sd(df_wohtn$SBP))
lines(SBPrange, ND, lwd=2)
# 3) Shapiro-Wilk test 시행하기
shapiro.test(df_wohtn$SBP)
##등분산성 검정
#F test
var.test(SBP~HTN, data=df)
#Levene의 등분산 검정
install.packages("lawstat")
library("lawstat")
levene.test(df$SBP, df$HTN, location="mean")
##T-test
t.test(df_wohtn$SBP, df_whtn$SBP, var.equal=TRUE)
R 독립 표본 T검정 (Dependent samples T-test, Two samples T-test) 정복 완료!
작성일: 2022.11.12.
최종 수정일: 2022.11.30.
이용 프로그램: R 4.2.2
RStudio v2022.07.2
RStudio 2022.07.2+576 "Spotted Wakerobin" Release
운영체제: Windows 10, Mac OS 12.6.1