[R] 크루스칼 왈리스 검정 (비모수 일원 배치 분산 분석: Kruskal-Wallis Test) - kruskal.test(), pairwise.wilcox.test(), ConoverTest(), DunnTest(), NemenyiTest()
셋 이상의 분포에서 평균이 다른지 확인하는 방법은 ANOVA (ANalysis Of VAriance)였다.
그런데, 여기에는 각각의 분포가 정규성을 따른다는 중요한 가정이 필요하다. 하지만 정규성을 따르지 않는다면 어떻게 해야 할까? 그럴 때 사용하는 것이 크루스칼-왈리스 검정(Kruskal-Wallis Test)이다. 이번 포스팅에서는 크루스칼 왈리스 검정과 그 사후 분석 (post hoc analysis)까지 알아보고자 한다.
*실습용 데이터는 아래 링크를 클릭하면 다운로드할 수 있습니다.
2022.08.04 - [공지사항 및 소개] - 분석용 데이터 (update 22.12.01)
분석용 데이터 (update 22.12.01)
2022년 12월 01일 버전입니다. 변수는 계속하여 추가될 예정입니다. 다음 카테고리에 있는 글에서 이용된 데이터입니다. - 기술 통계 - 범주형 자료 분석 - 모평균 검정 - 반복 측정 자료 분석 - 통계
medistat.tistory.com
코드를 보여드리기에 앞서 워킹 디렉토리부터 지정하겠다.
워킹 디렉토리에 관한 설명은 다음 링크된 포스트에서 볼 수 있다.
2022.08.05 - [통계 프로그램 사용 방법/R] - [R] 작업 디렉토리 (Working Directory) 지정 - getwd(), setwd()
setwd("C:/Users/user/Documents/Tistory_blog")
데이터를 불러와 df에 객체로 저장하겠다.
데이터 불러오는 방법은 다음 링크에서 볼 수 있다.
2022.08.05 - [통계 프로그램 사용 방법/R] - [R] 데이터 불러오기 : EXCEL - read_excel(), read.xlsx()
2022.08.10 - [통계 프로그램 사용 방법/R] - [R] 데이터 저장하기 : CSV 파일 - write.csv(), write_csv()
2022.08.10 - [통계 프로그램 사용 방법/R] - [R] 데이터 불러오기 : SAS file (.sas7bdat) - read.sas7bdat(), read_sas()
install.packages("readr")
library("readr")
df<-read_csv("Data.csv")
목표: 흡연 상태(SMOK)에 따라 니코틴 중독 점수 (NICOT_ADDICT) 중앙값이 모집단 수준에서 서로 다르다고 말할 수 있는가?
만약 NICOT_ADDICT의 분포가 정규성을 따른다면, ANOVA로 이를 확인할 수 있을 것이다. 따라서 정규성 여부를 먼저 확인해보자.
1) 정규성 - 코드
흡연 상태 별로 NICOT_ADDICT의 정규성을 확인하기 위해서는 다음 두 가지의 일을 해야 한다.
1) 흡연 상태에 따라 데이터를 나누기
2) 각각 정규성을 확인하기.
1)데이터 나누기
조건에 따라 데이터를 나누는 방법에 대한 설명은 다음 링크에서 볼 수 있다. 2022.11.10 - [통계 프로그램 사용 방법/R] - [R] 조건에 맞는 자료 추출하기
위 링크에서 확인할 수 있듯이 여러 가지 방법으로 나눌 수 있지만 indexing을 이용하여 나누도록 하겠다.
dfne<-df[df$SMOK==0,]
dffo<-df[df$SMOK==1,]
dfcu<-df[df$SMOK==2,]dfne: 비흡연자의 데이터
dffo: 과거 흡연자의 데이터
dfcu: 현재 흡연자의 데이터
2) 정규성 확인
정규성 검정에 관한 내용은 다음 링크에서 확인할 수 있다.
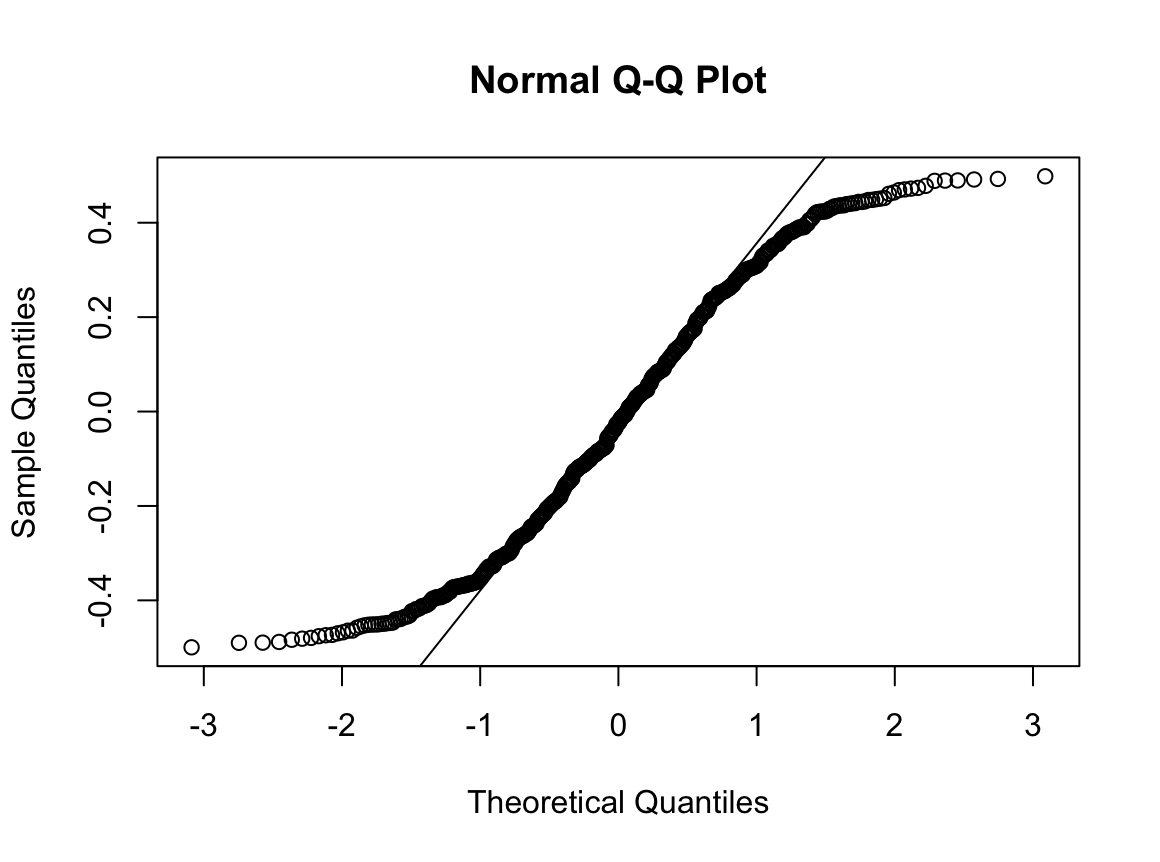
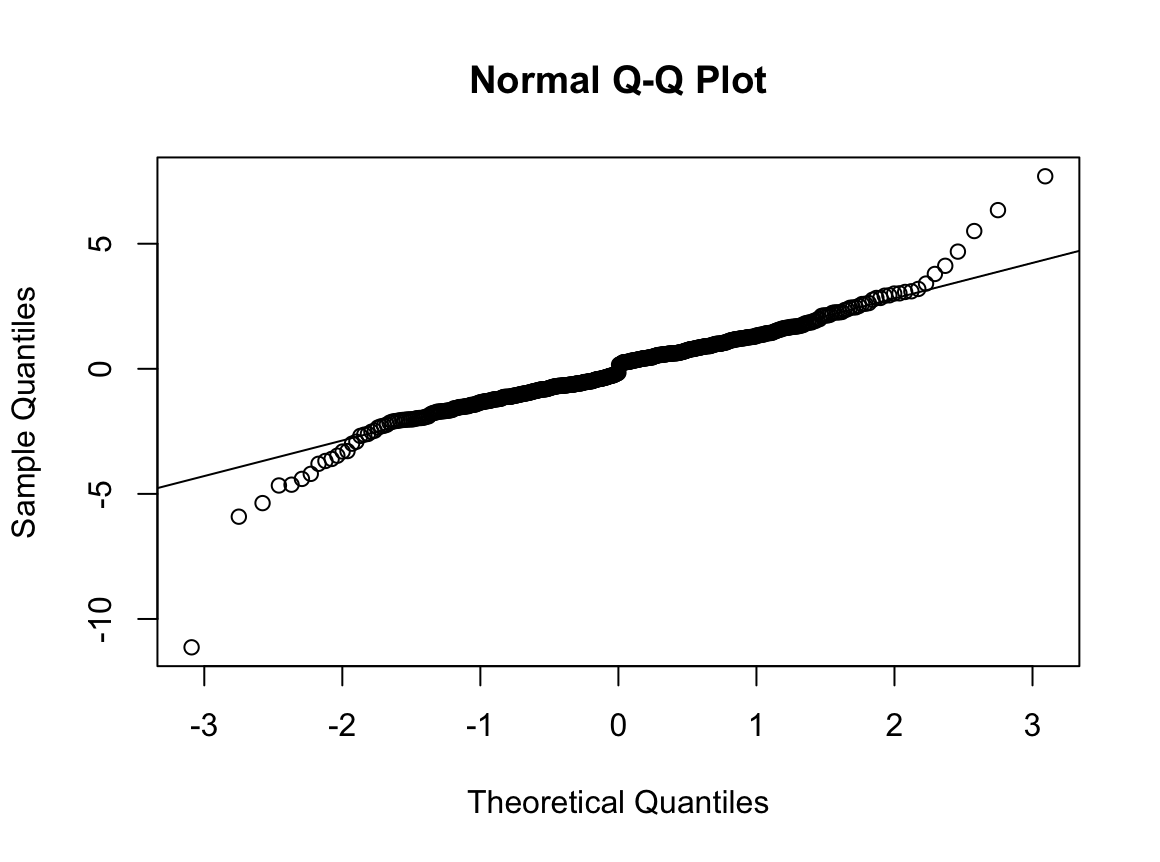
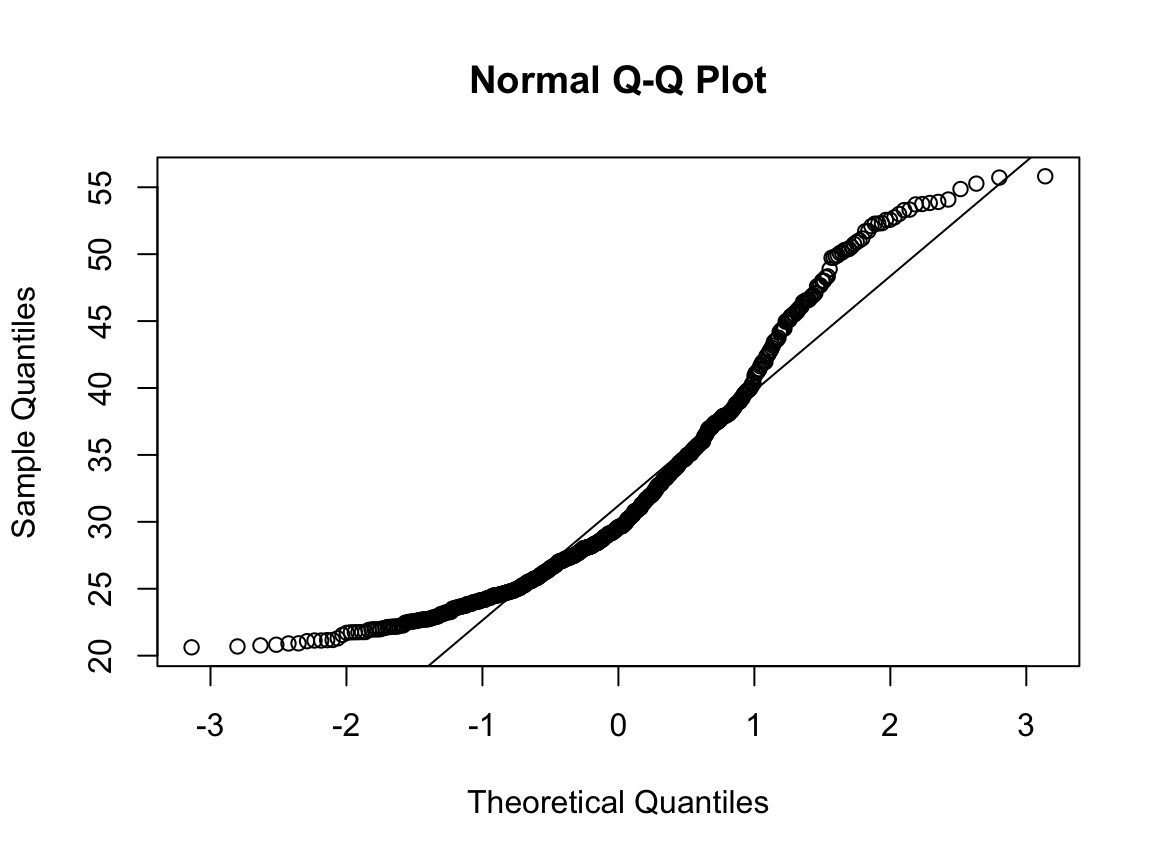
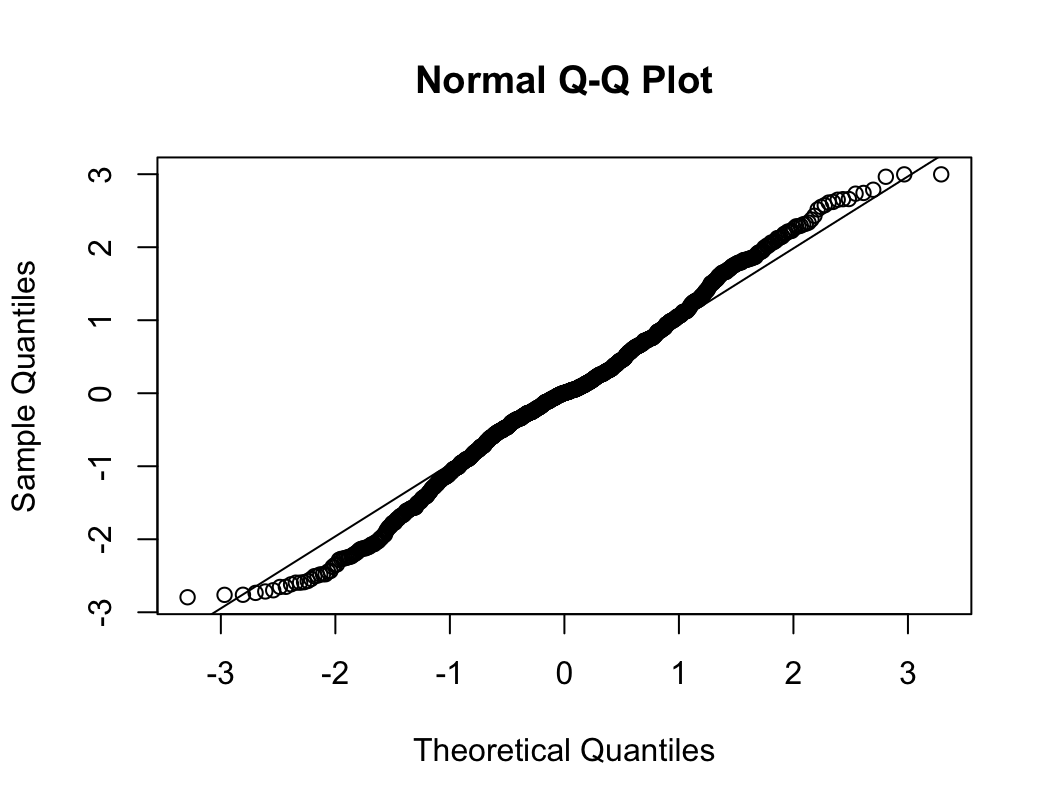
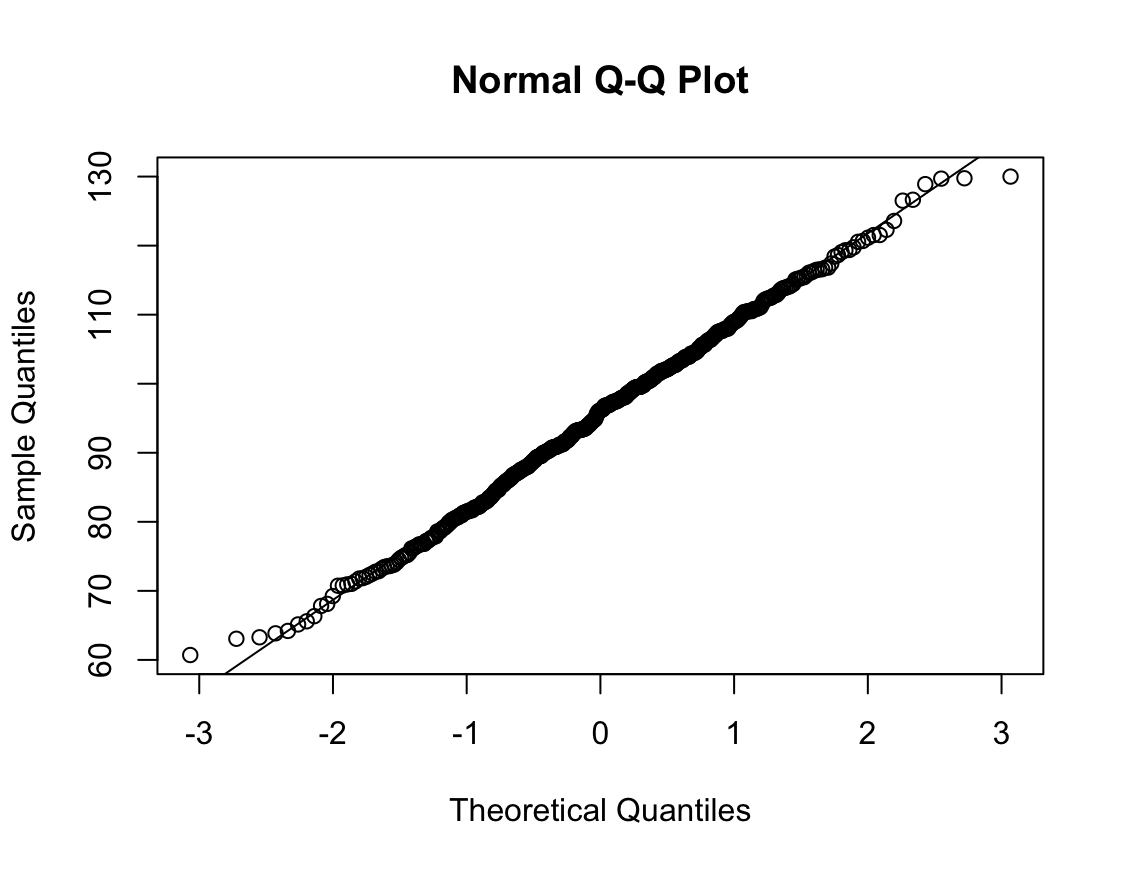
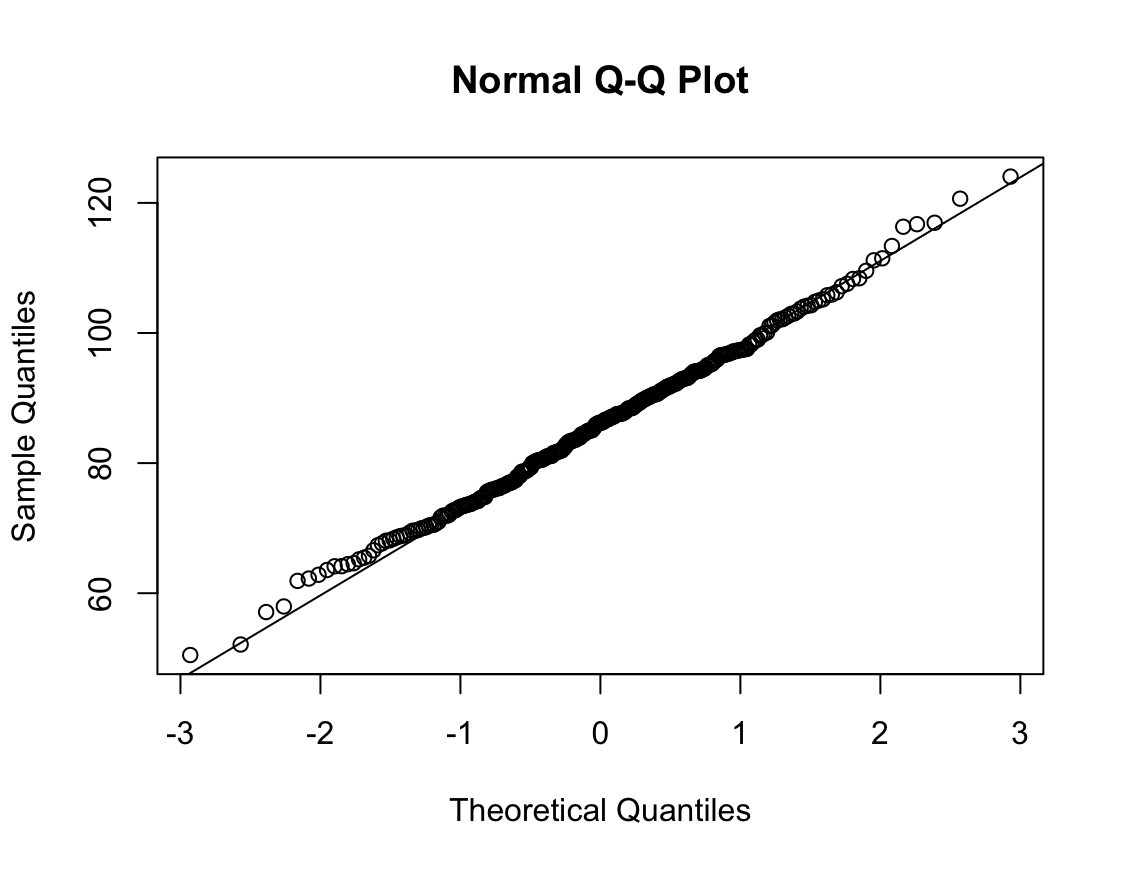
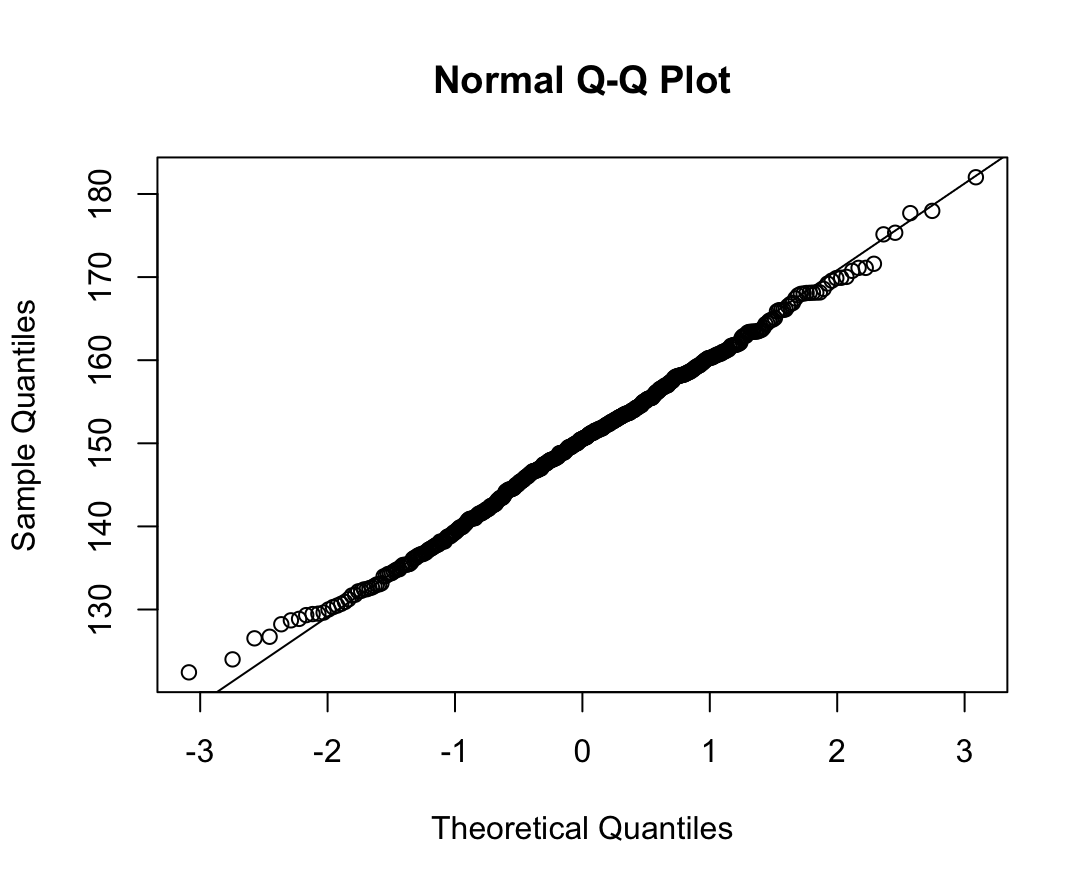
2022.08.11 - [기술 통계/R] - [R] 정규성 검정 (1) : Q-Q plot - qqnorm(), qqline()
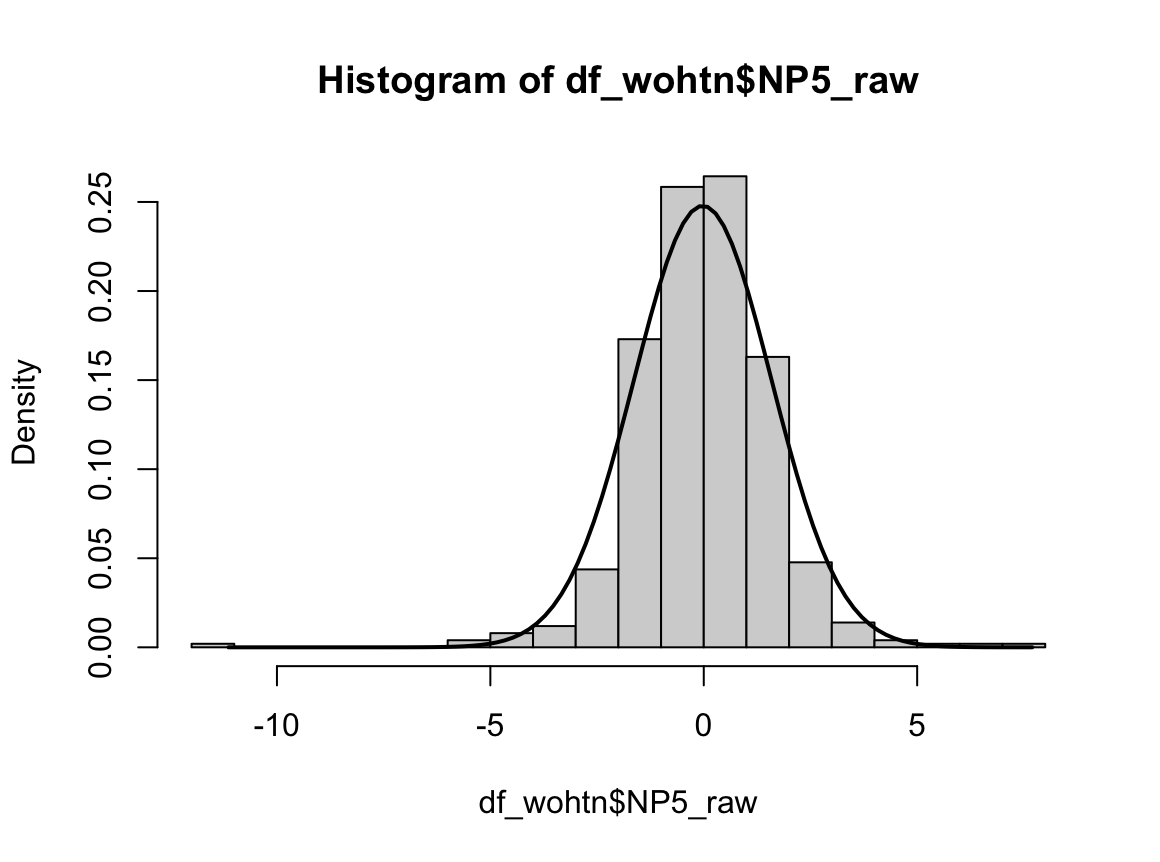
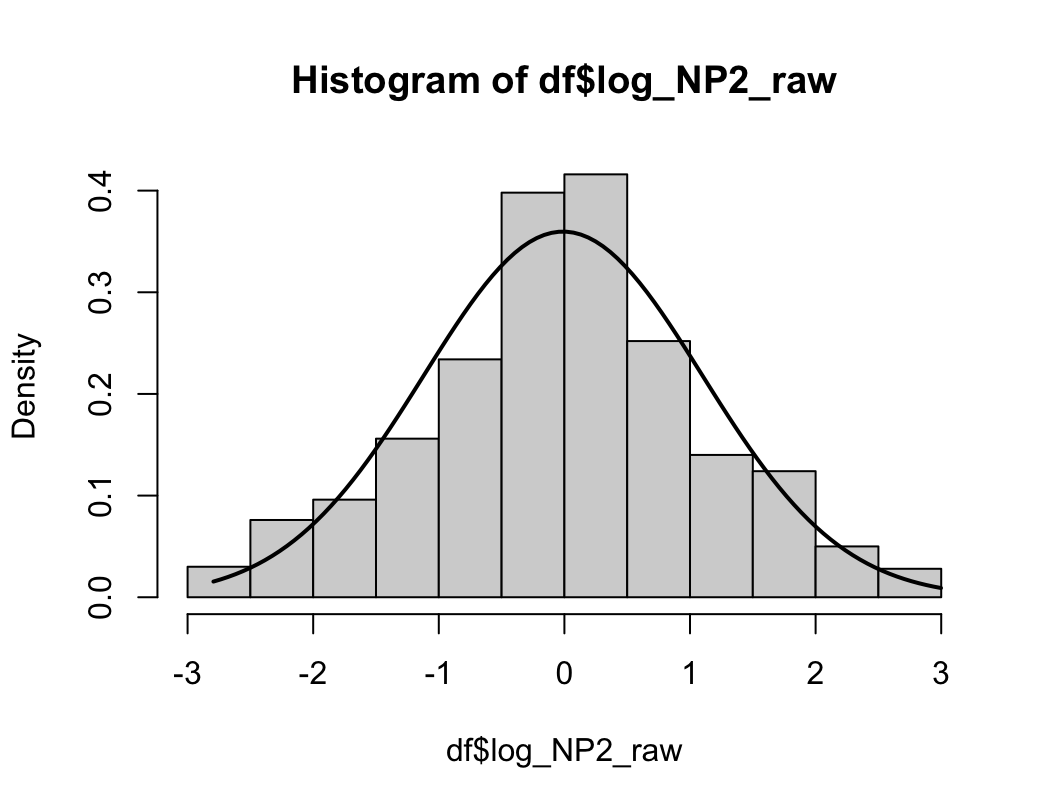
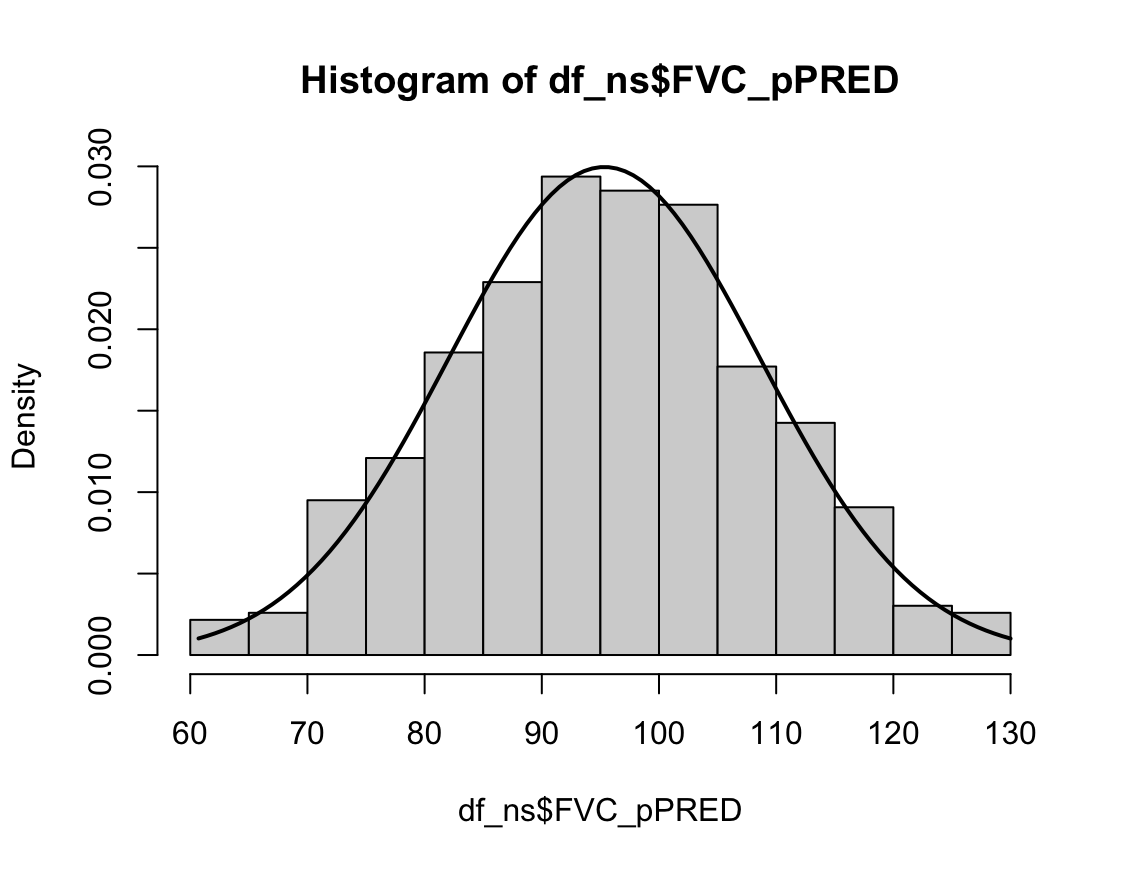
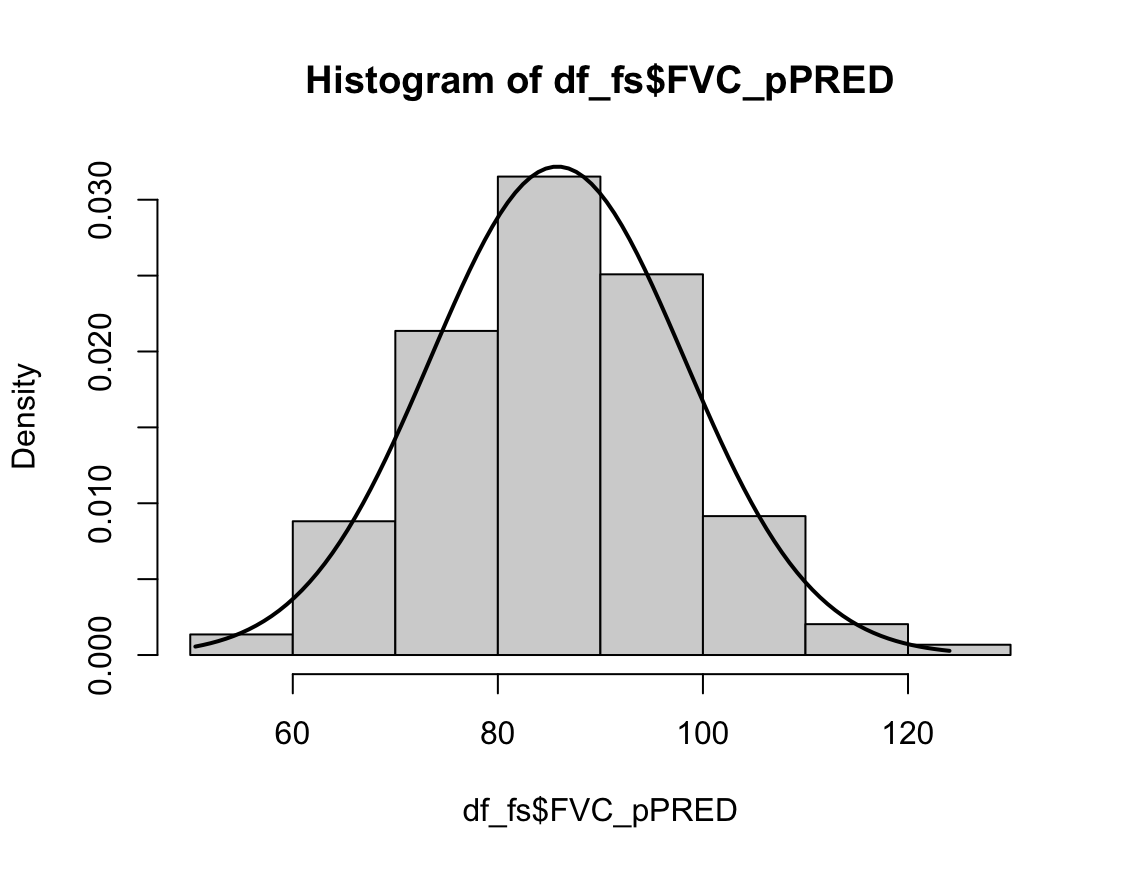
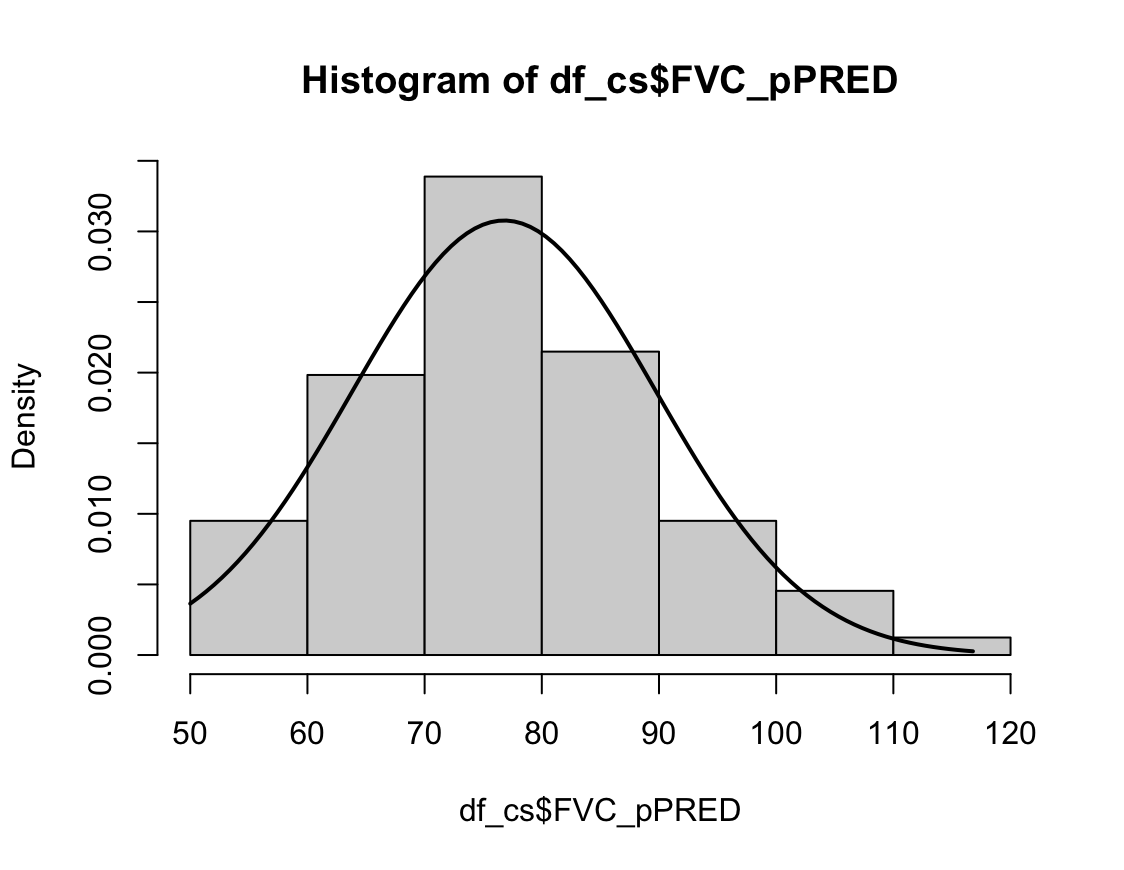
2022.08.11 - [기술 통계/R] - [R] 정규성 검정 (2) : 히스토그램 - hist(), dnorm()
2022.08.12 - [기술 통계/R] - [R] 정규성 검정 (4) : 정량적 검정 (Lilliefors test) - lillie.test()
2022.08.16 - [기술 통계/R] - [R] 고급 Q-Q Plot - Van der Waerden, Rankit, Tukey, Blom
#비흡연자
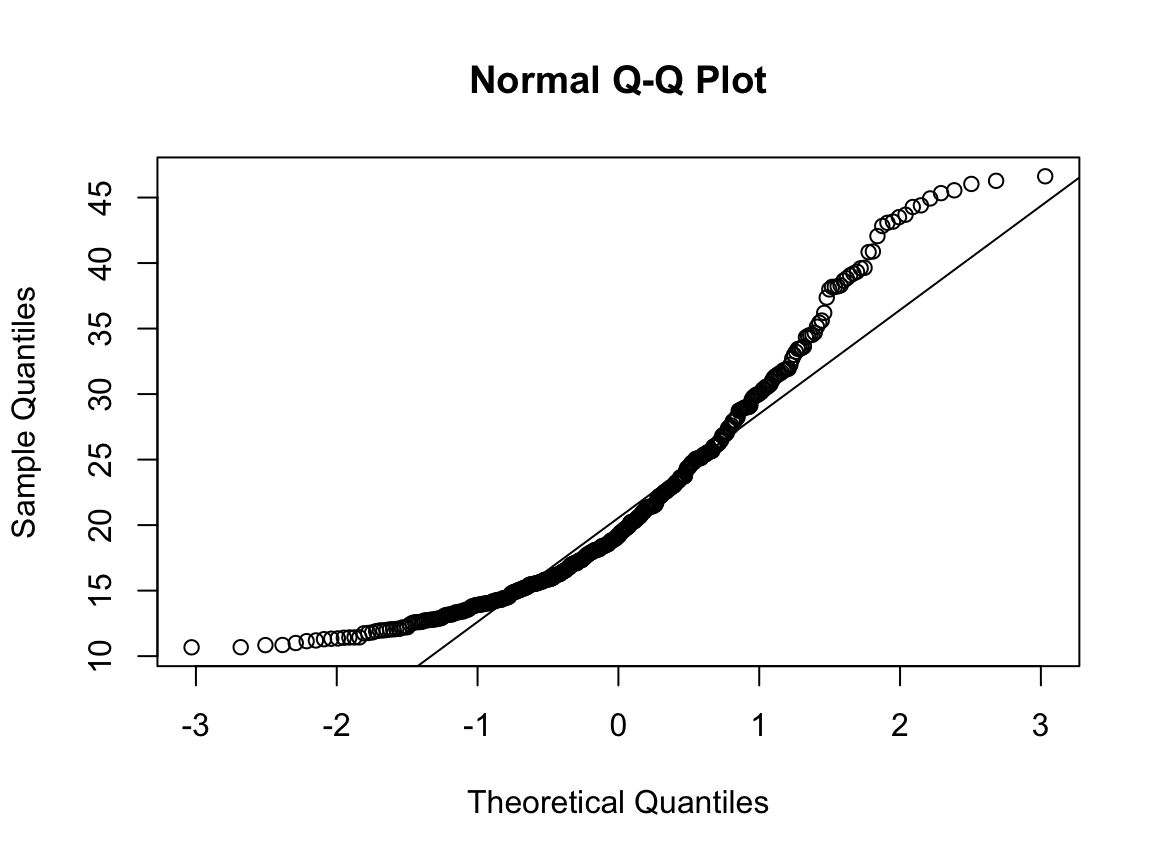
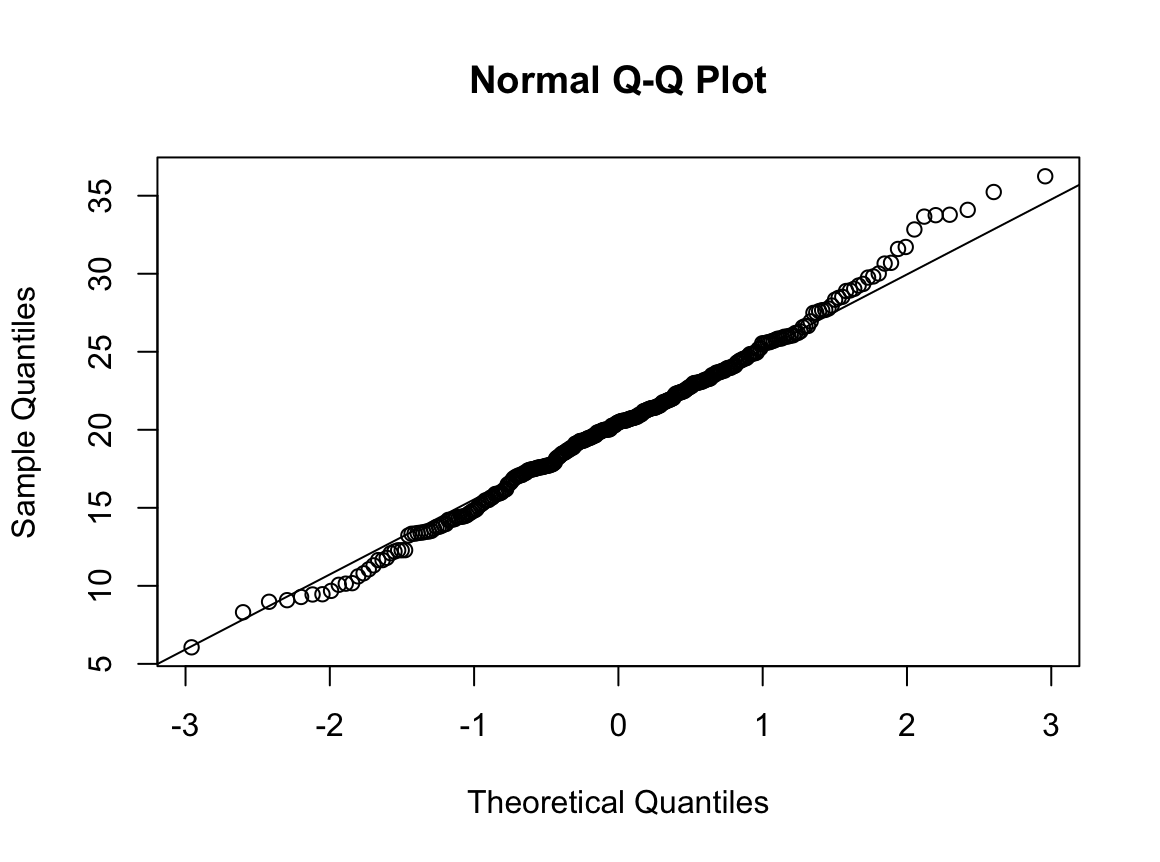
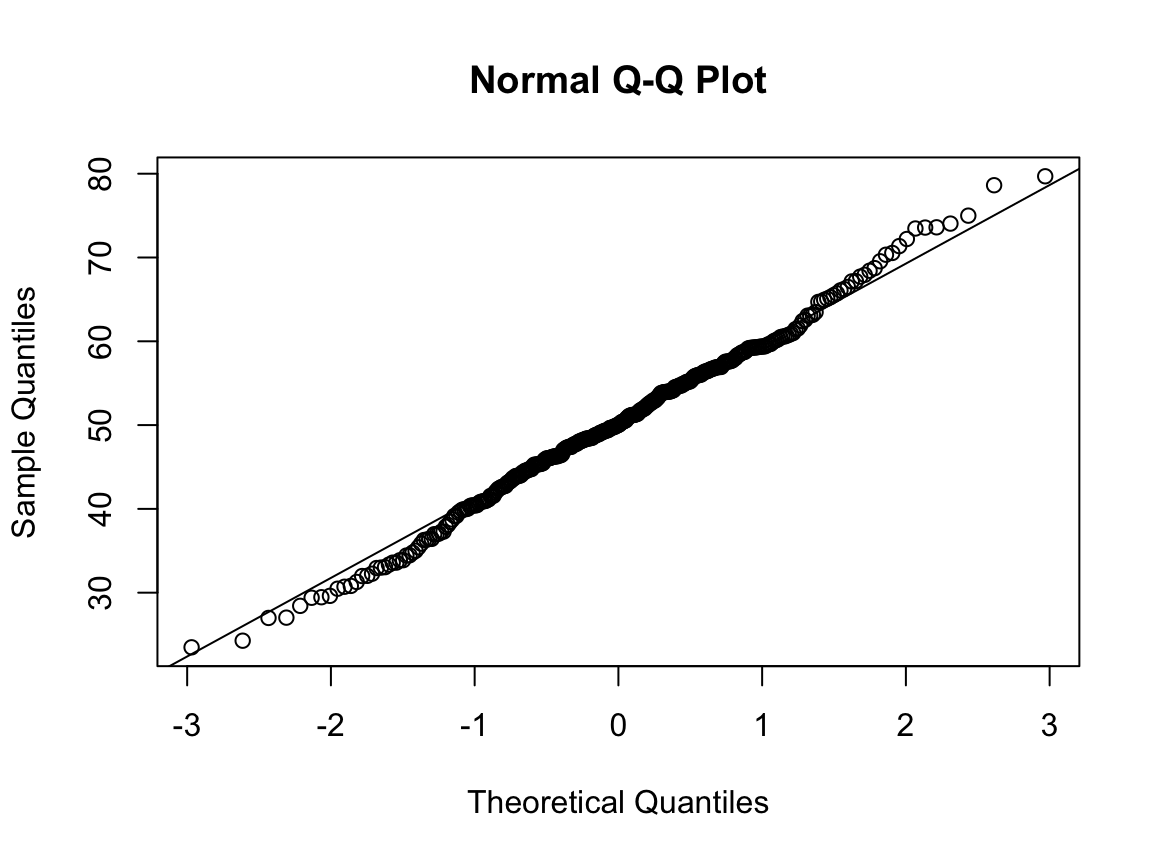
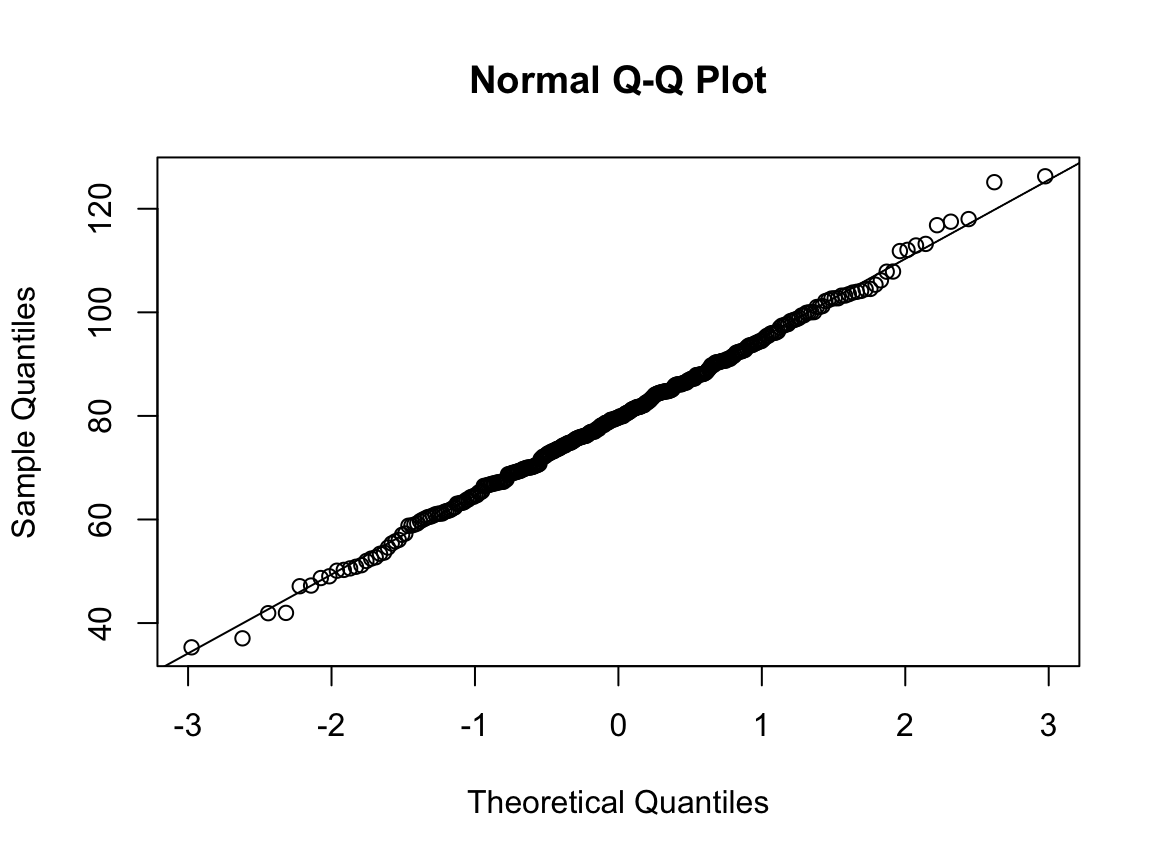
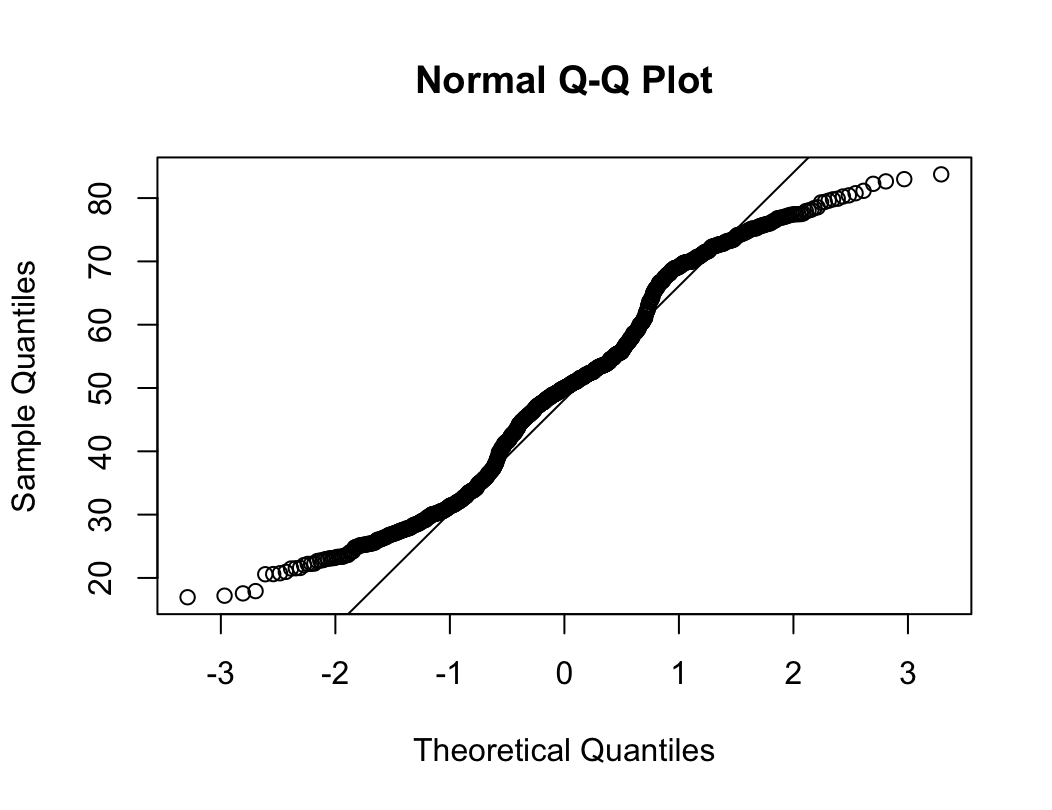
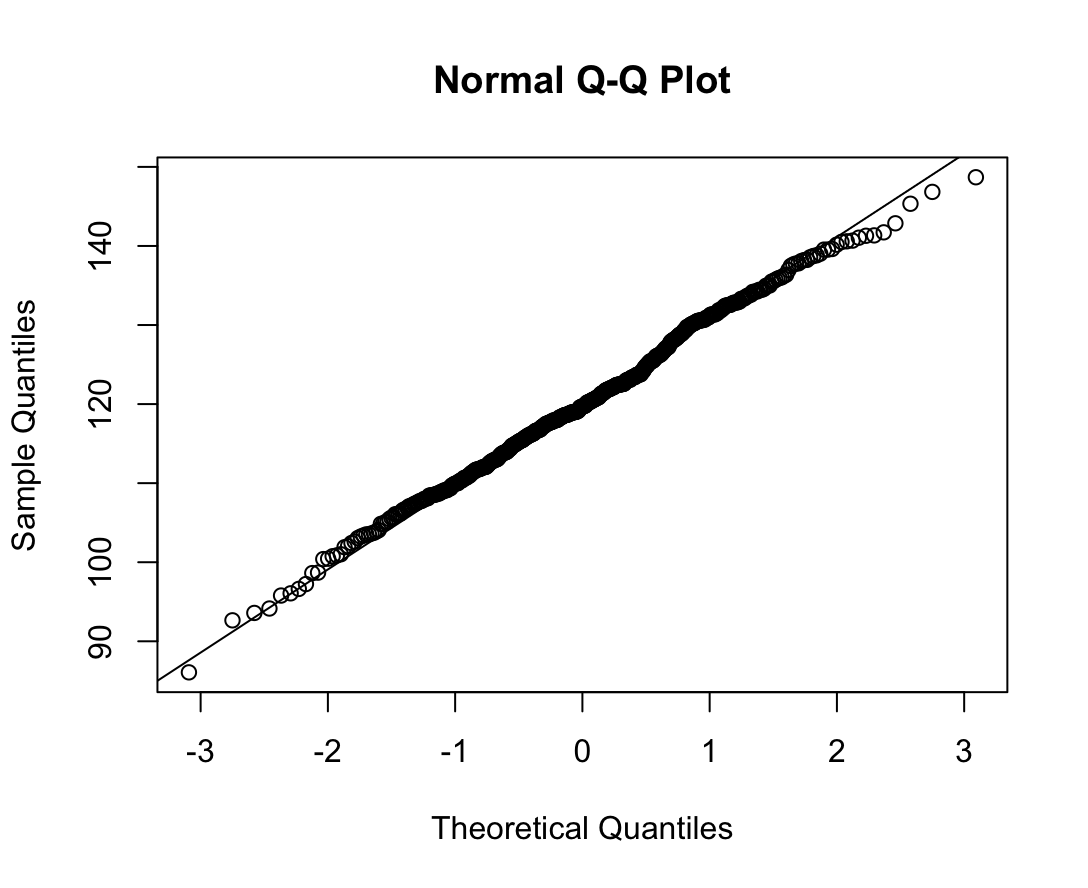
# 1) Q-Q plot 그리기
qqnorm(dfne$NICOT_ADDICT)
qqline(dfne$NICOT_ADDICT)
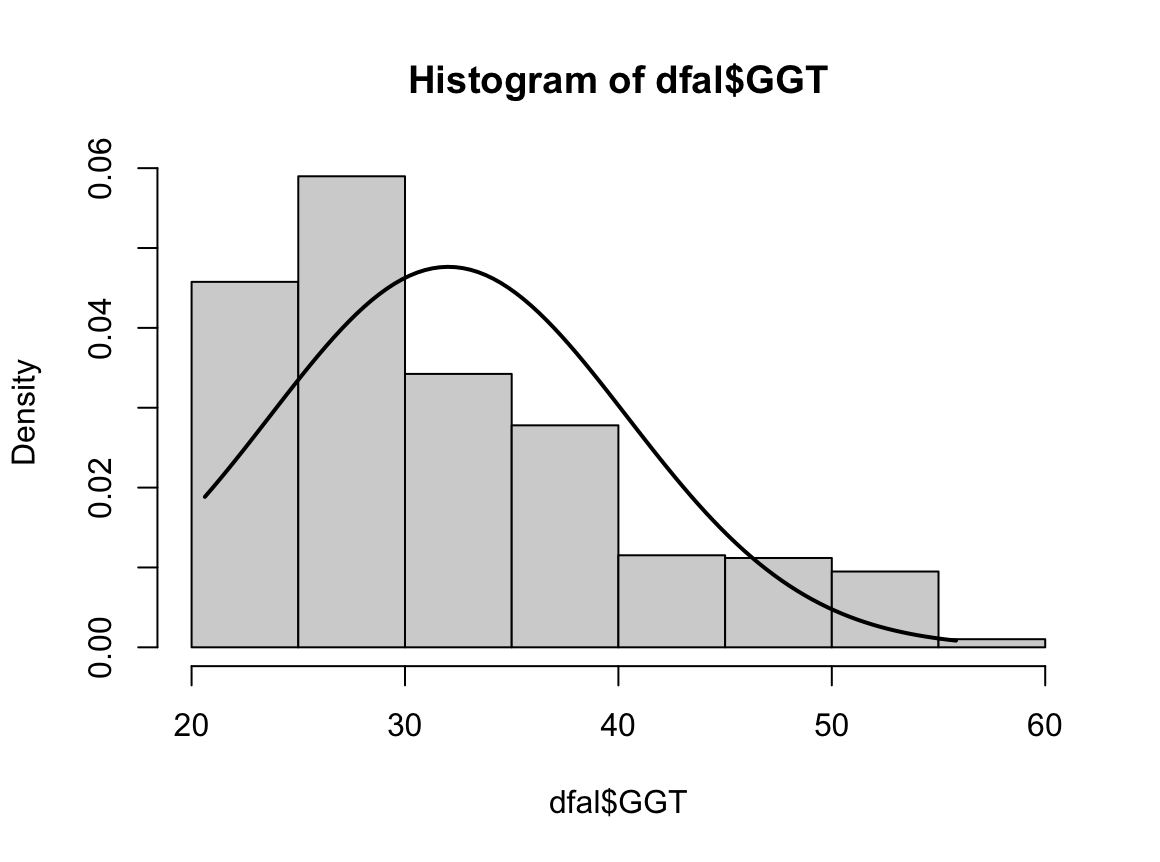
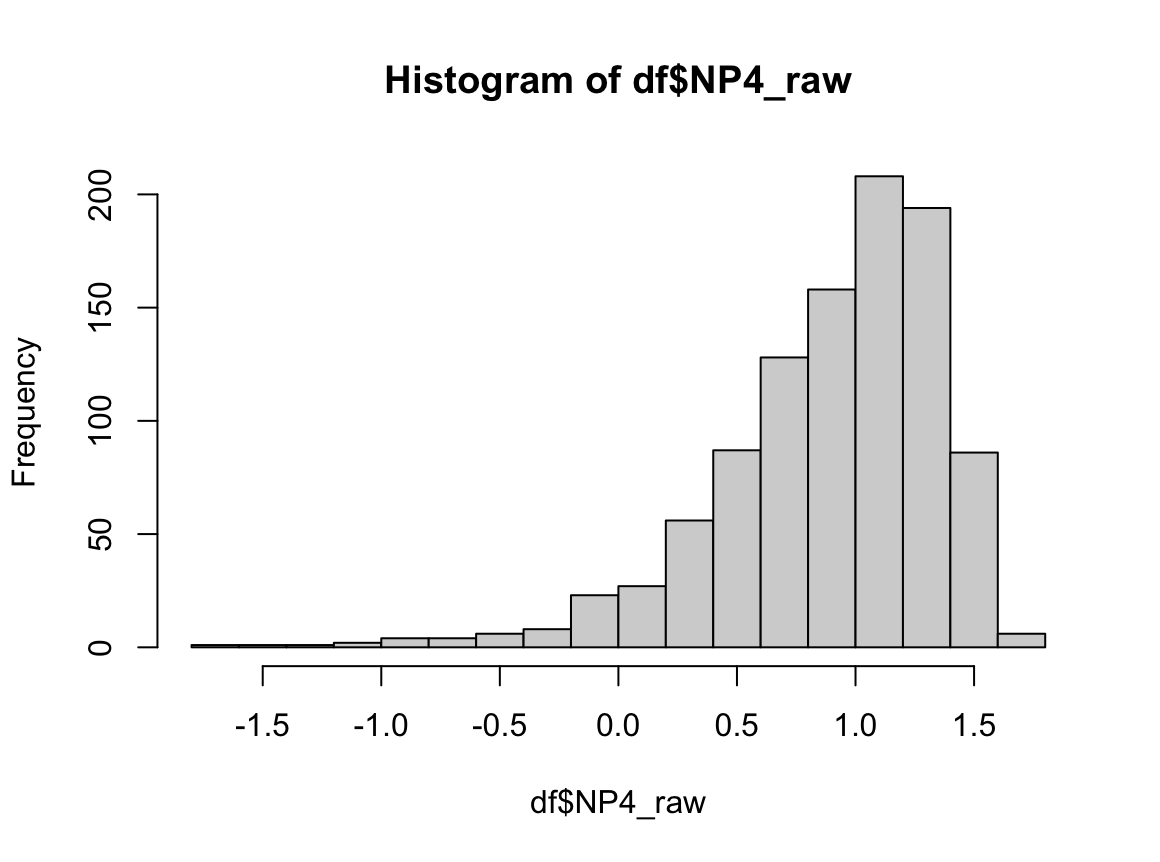
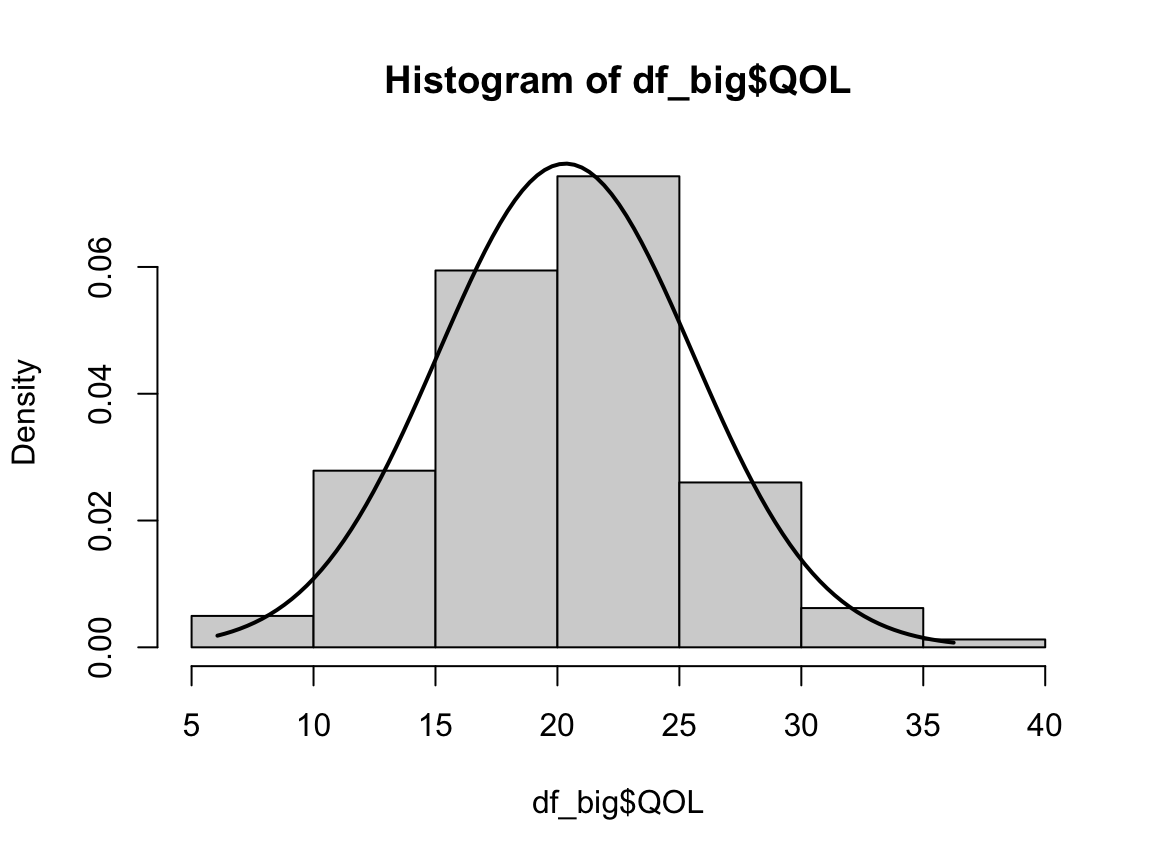
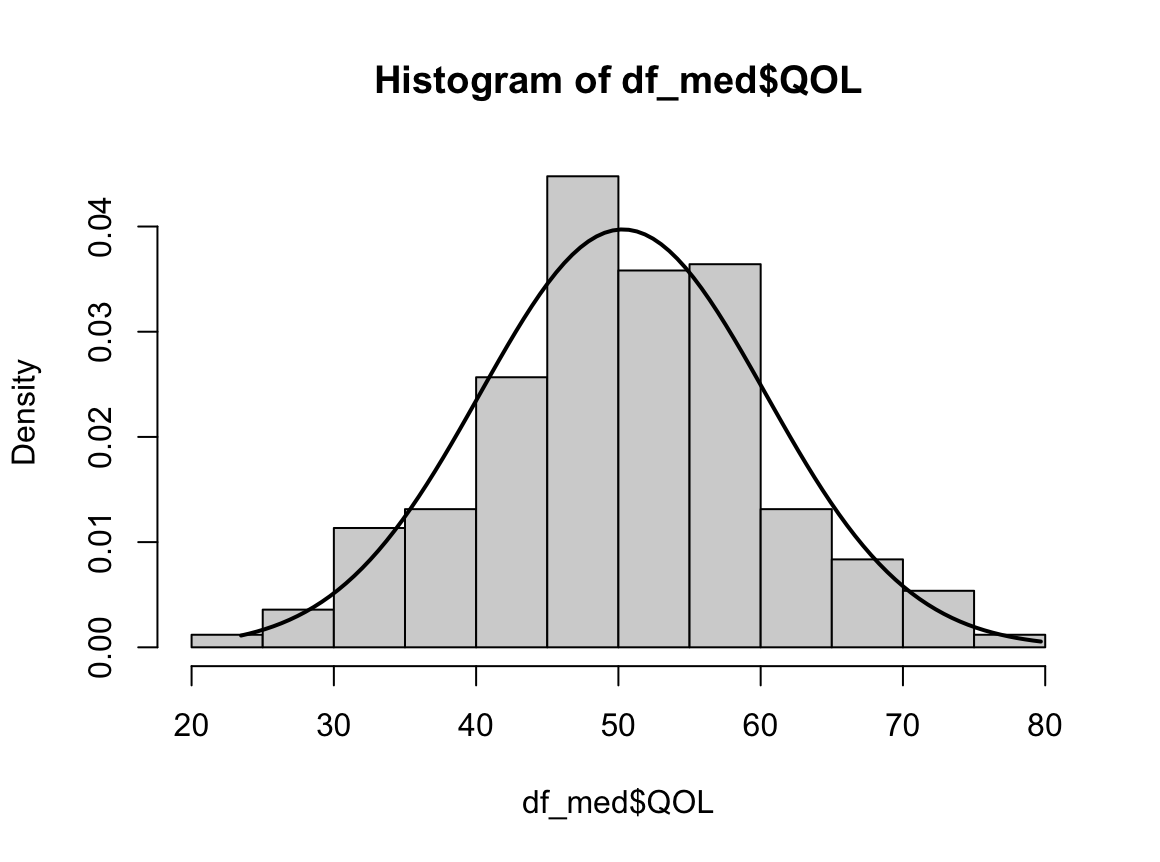
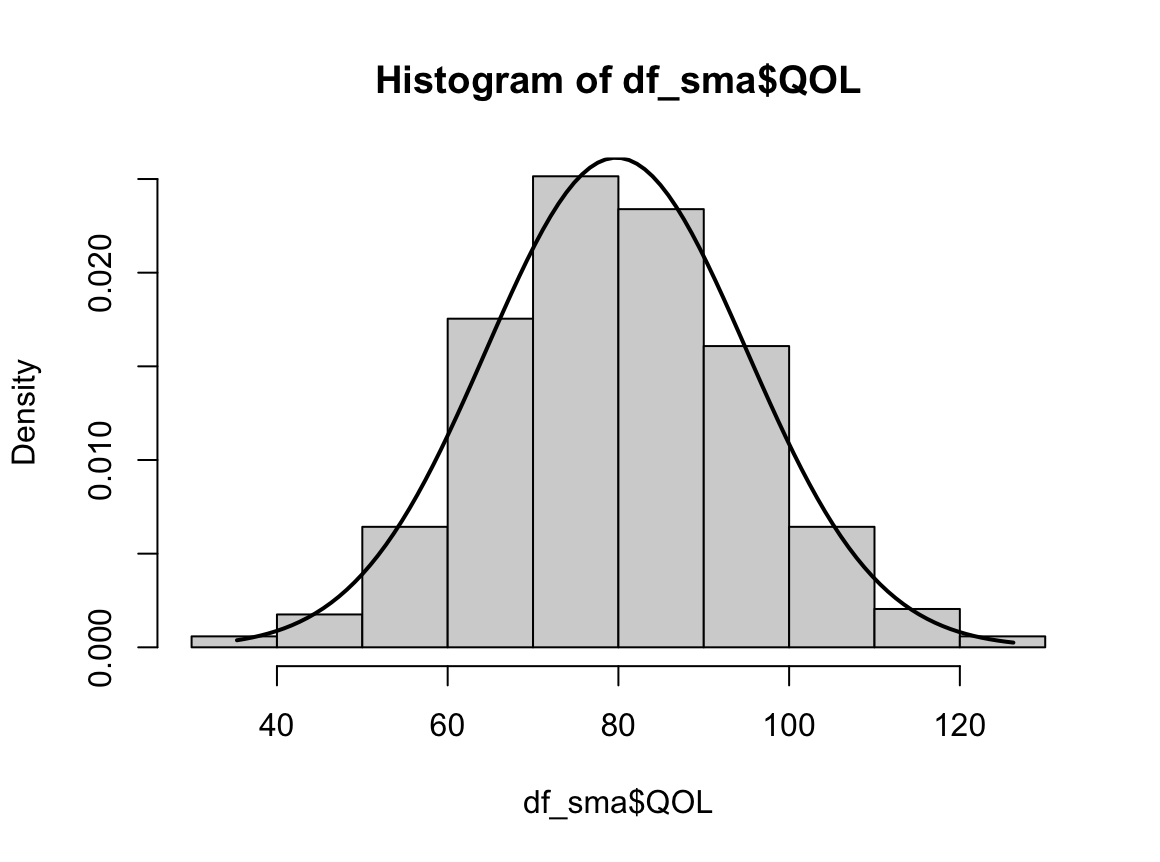
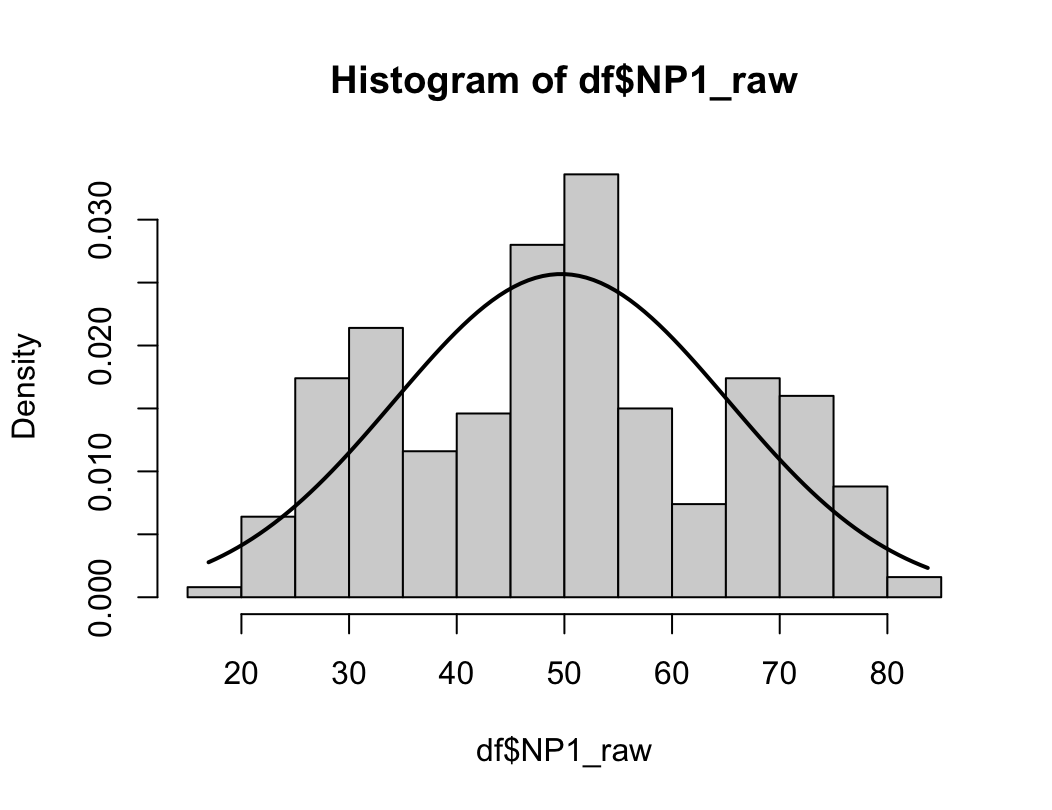
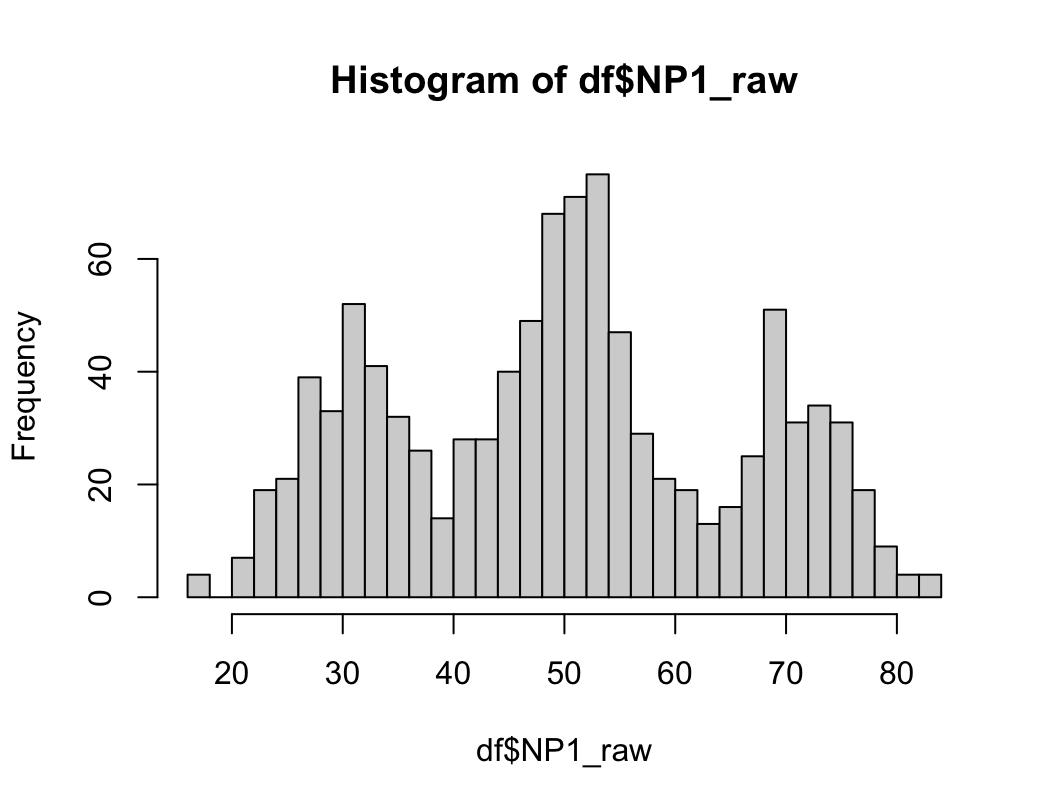
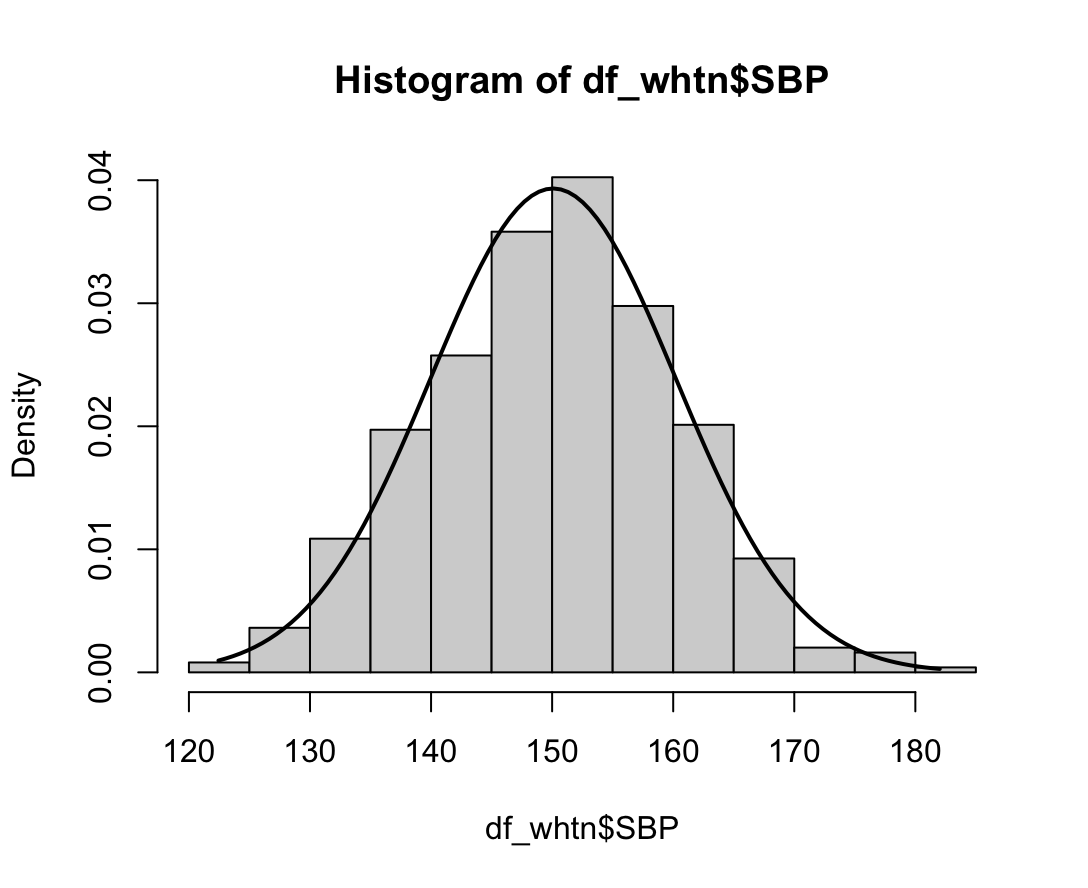
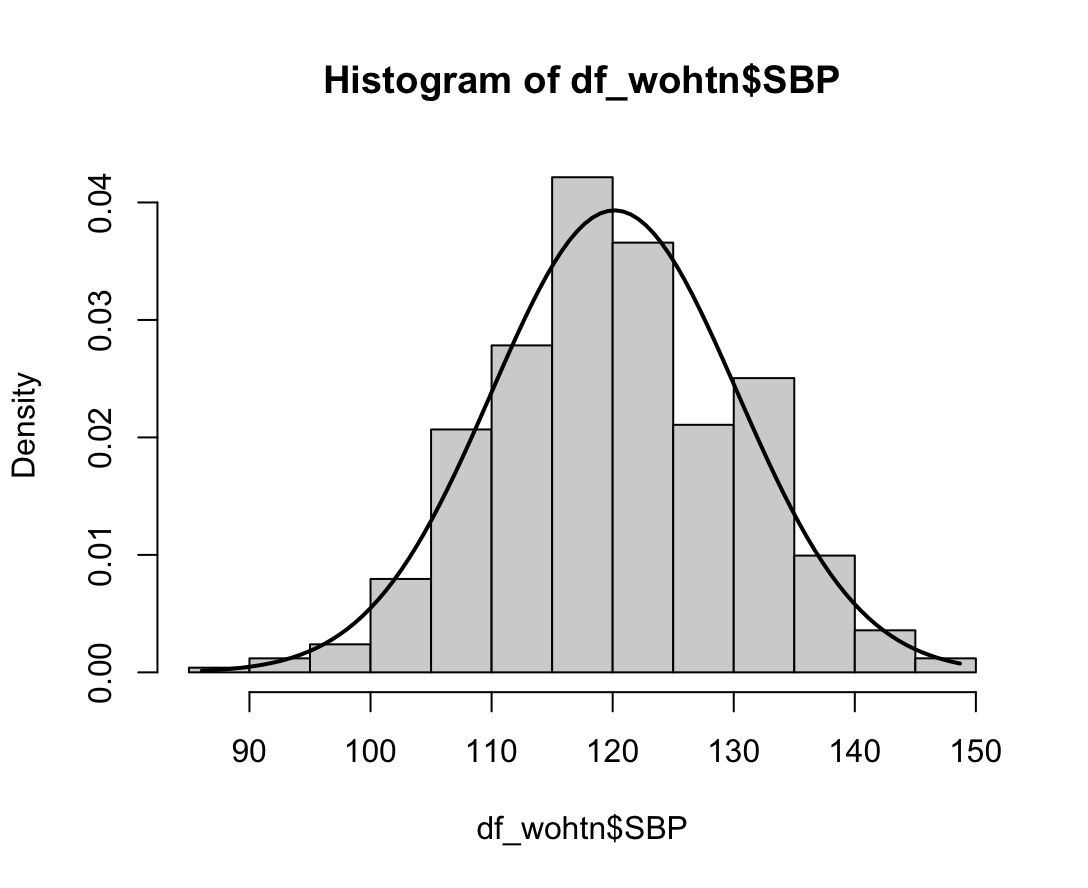
# 2) 히스토그램 그리기
hist(dfne$NICOT_ADDICT, prob=TRUE)
NICOT_ADDICTrange<-seq(min(dfne$NICOT_ADDICT),max(dfne$NICOT_ADDICT),length=max(max(dfne$NICOT_ADDICT)-min(dfne$NICOT_ADDICT),100))
ND<-dnorm(NICOT_ADDICTrange,mean=mean(dfne$NICOT_ADDICT),sd=sd(dfne$NICOT_ADDICT))
lines(NICOT_ADDICTrange, ND, lwd=2)
# 3) Shapiro-Wilk test 시행하기
shapiro.test(dfne$NICOT_ADDICT)
#과거 흡연자
# 1) Q-Q plot 그리기
qqnorm(dffo$NICOT_ADDICT)
qqline(dffo$NICOT_ADDICT)
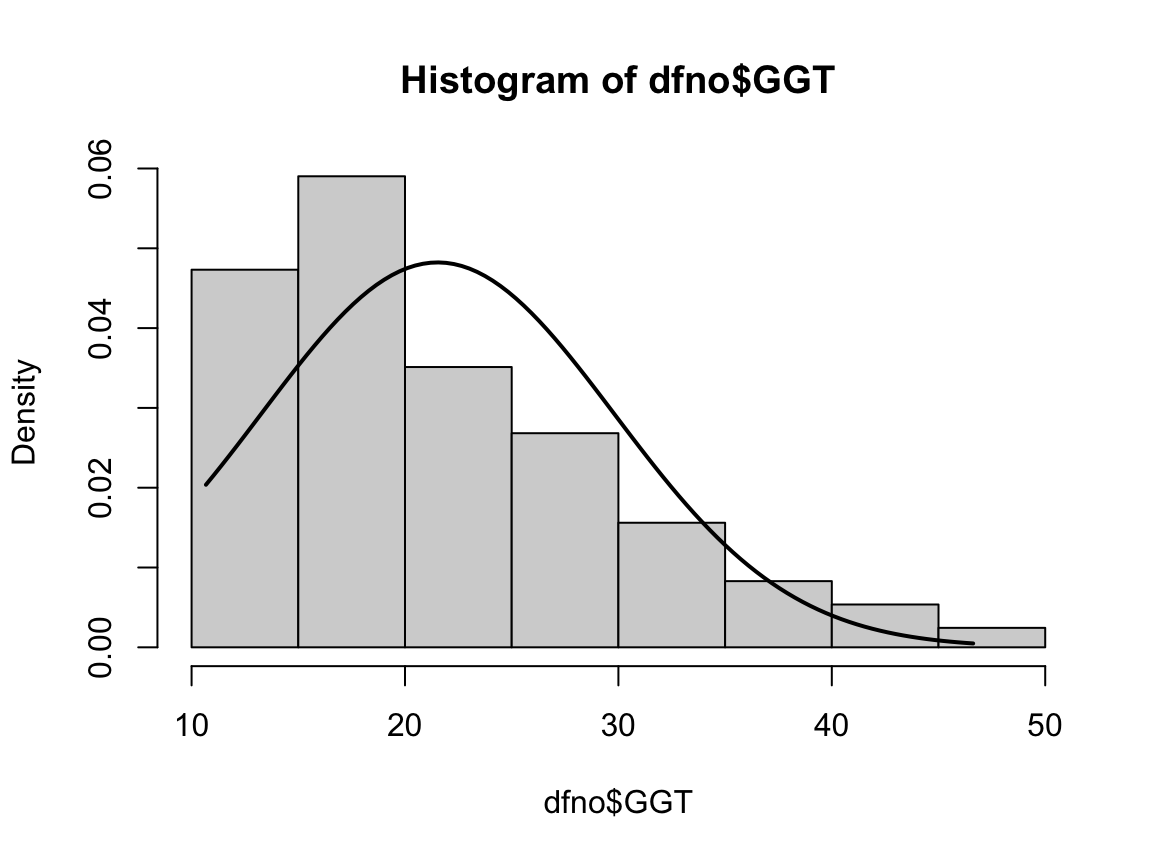
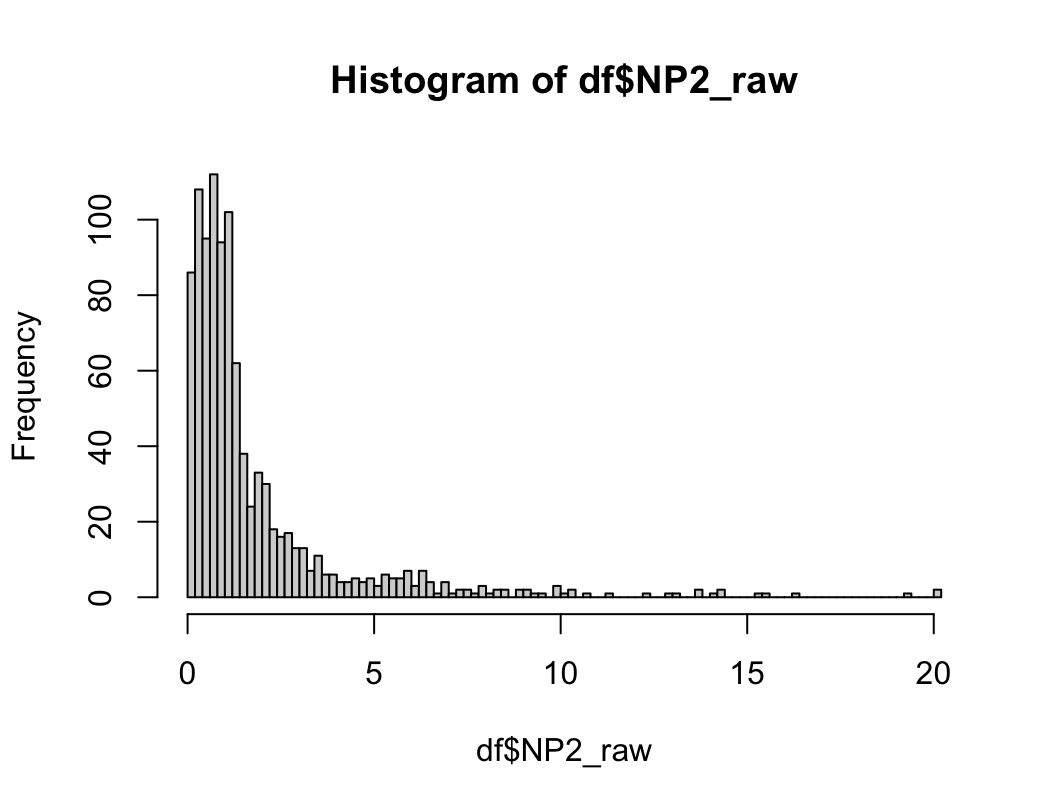
# 2) 히스토그램 그리기
hist(dffo$NICOT_ADDICT, prob=TRUE)
NICOT_ADDICTrange<-seq(min(dffo$NICOT_ADDICT),max(dffo$NICOT_ADDICT),length=max(max(dffo$NICOT_ADDICT)-min(dffo$NICOT_ADDICT),100))
ND<-dnorm(NICOT_ADDICTrange,mean=mean(dffo$NICOT_ADDICT),sd=sd(dffo$NICOT_ADDICT))
lines(NICOT_ADDICTrange, ND, lwd=2)
# 3) Shapiro-Wilk test 시행하기
shapiro.test(dffo$NICOT_ADDICT)
#현재 흡연자
# 1) Q-Q plot 그리기
qqnorm(dfcu$NICOT_ADDICT)
qqline(dfcu$NICOT_ADDICT)
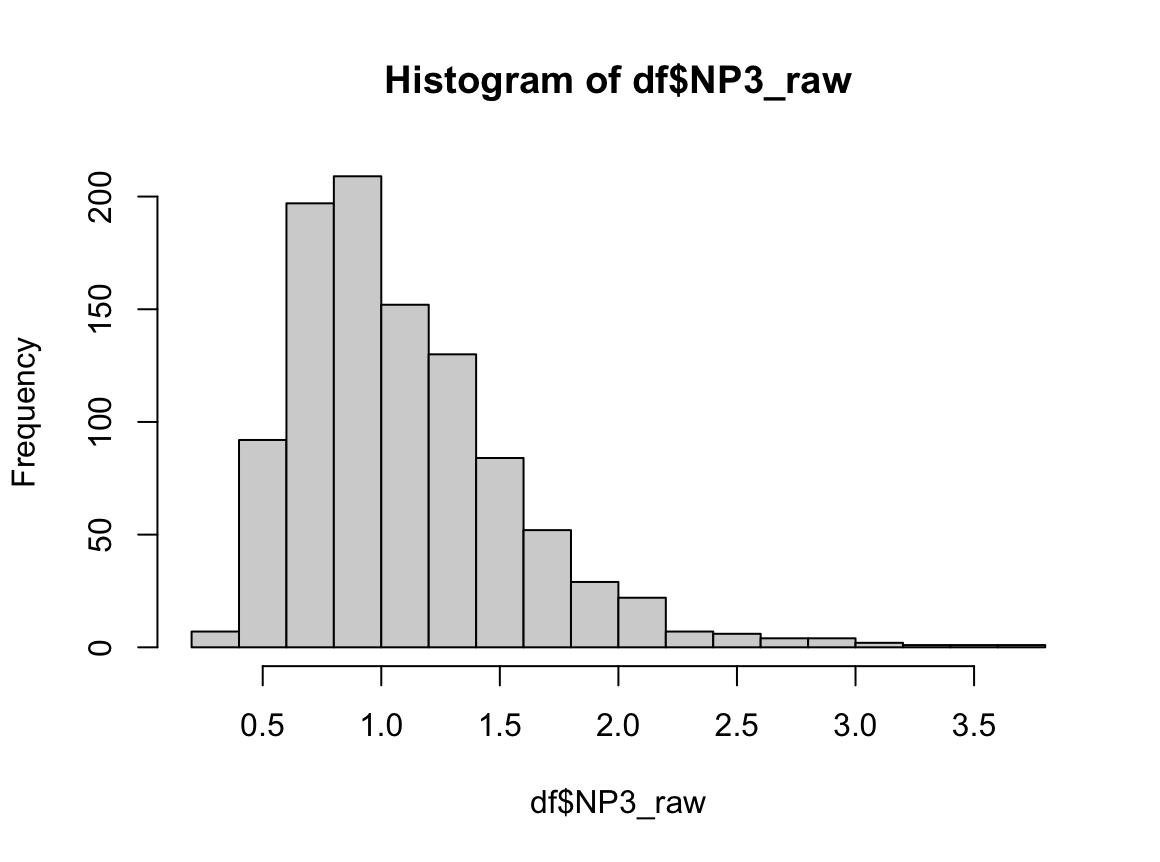
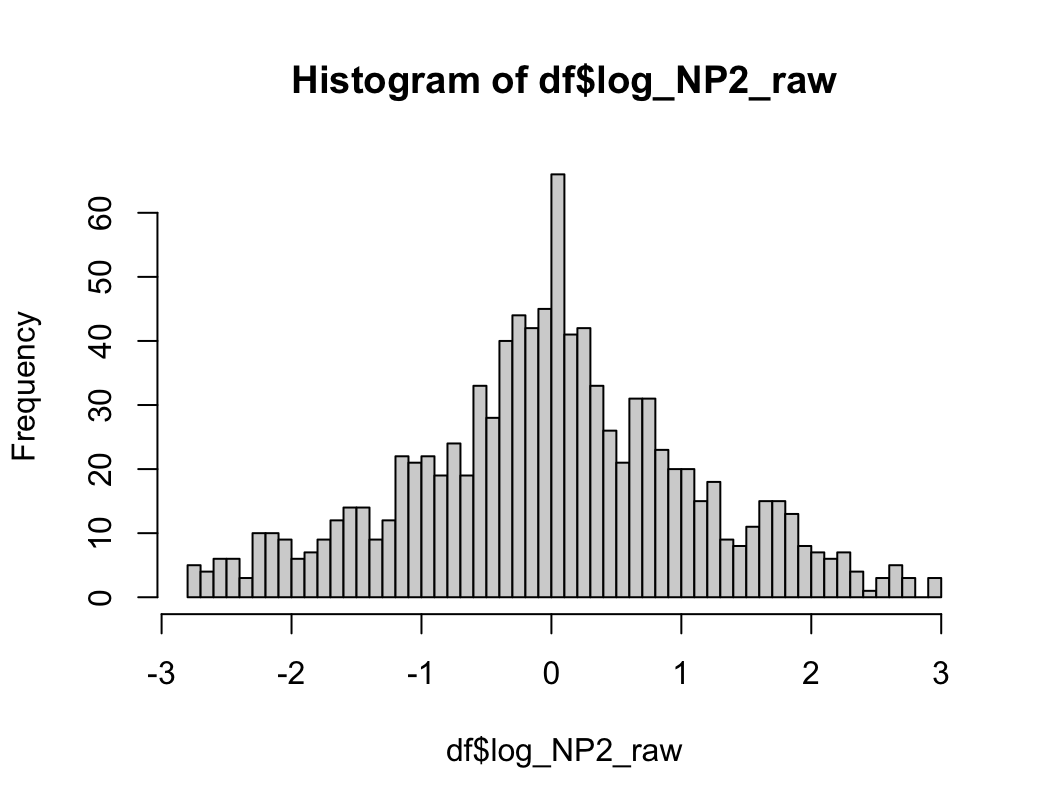
# 2) 히스토그램 그리기
hist(dfcu$NICOT_ADDICT, prob=TRUE)
NICOT_ADDICTrange<-seq(min(dfcu$NICOT_ADDICT),max(dfcu$NICOT_ADDICT),length=max(max(dfcu$NICOT_ADDICT)-min(dfcu$NICOT_ADDICT),100))
ND<-dnorm(NICOT_ADDICTrange,mean=mean(dfcu$NICOT_ADDICT),sd=sd(dfcu$NICOT_ADDICT))
lines(NICOT_ADDICTrange, ND, lwd=2)
# 3) Shapiro-Wilk test 시행하기
shapiro.test(dfcu$NICOT_ADDICT)
결과
1) 비흡연자
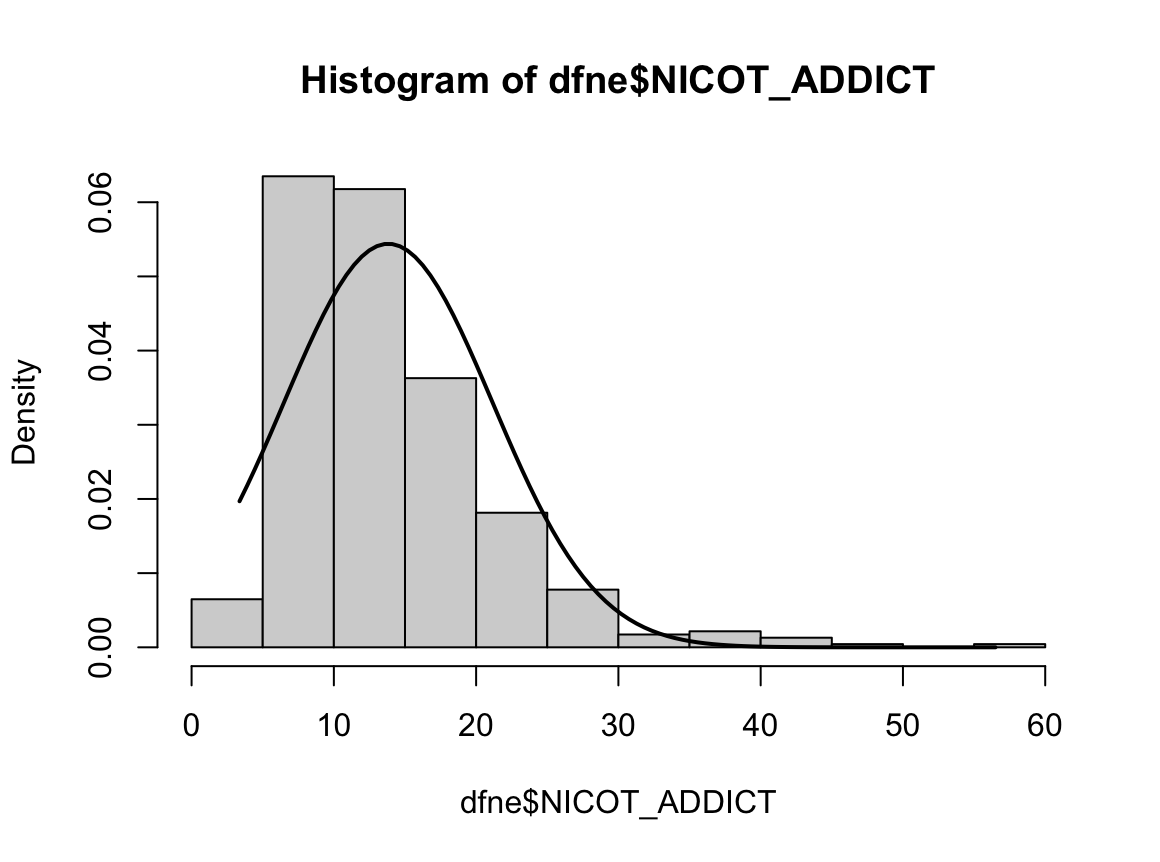
Shapiro-Wilk normality test
data: dfne$NICOT_ADDICT
W = 0.88076, p-value < 2.2e-16
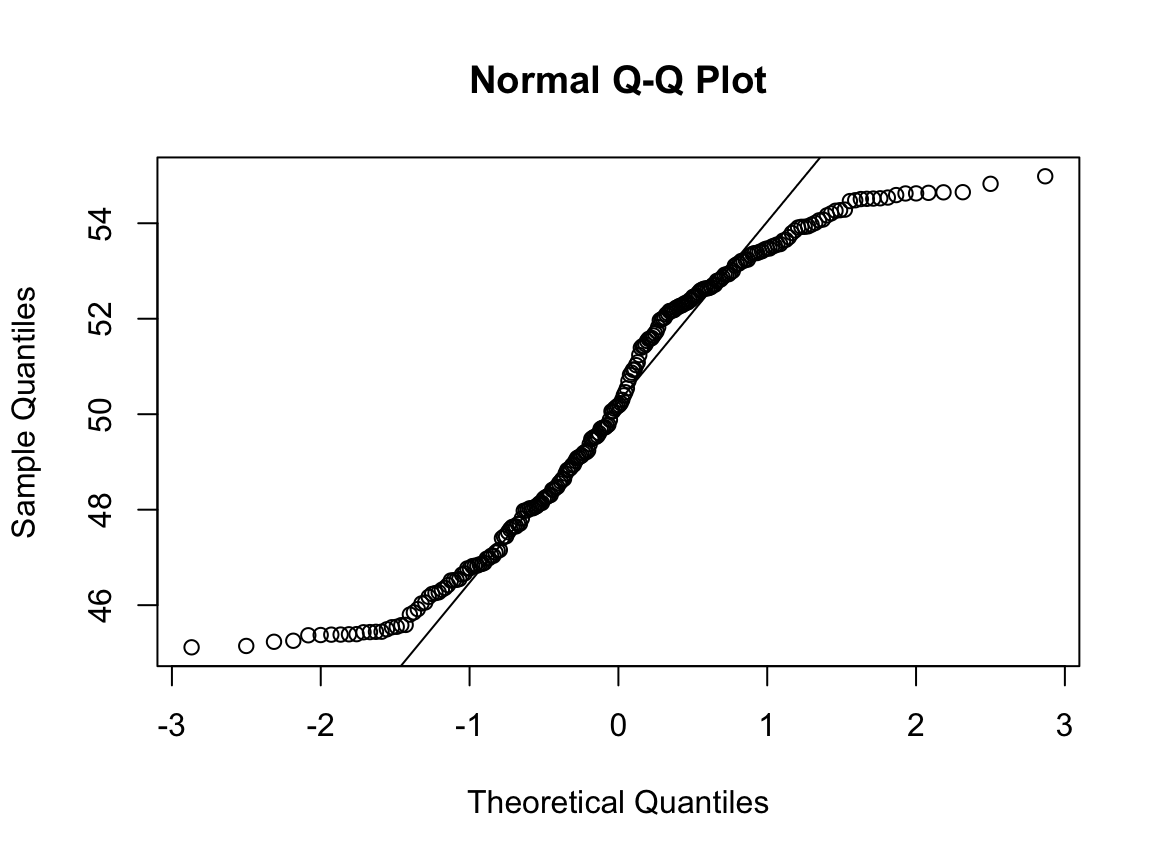
2) 과거 흡연자
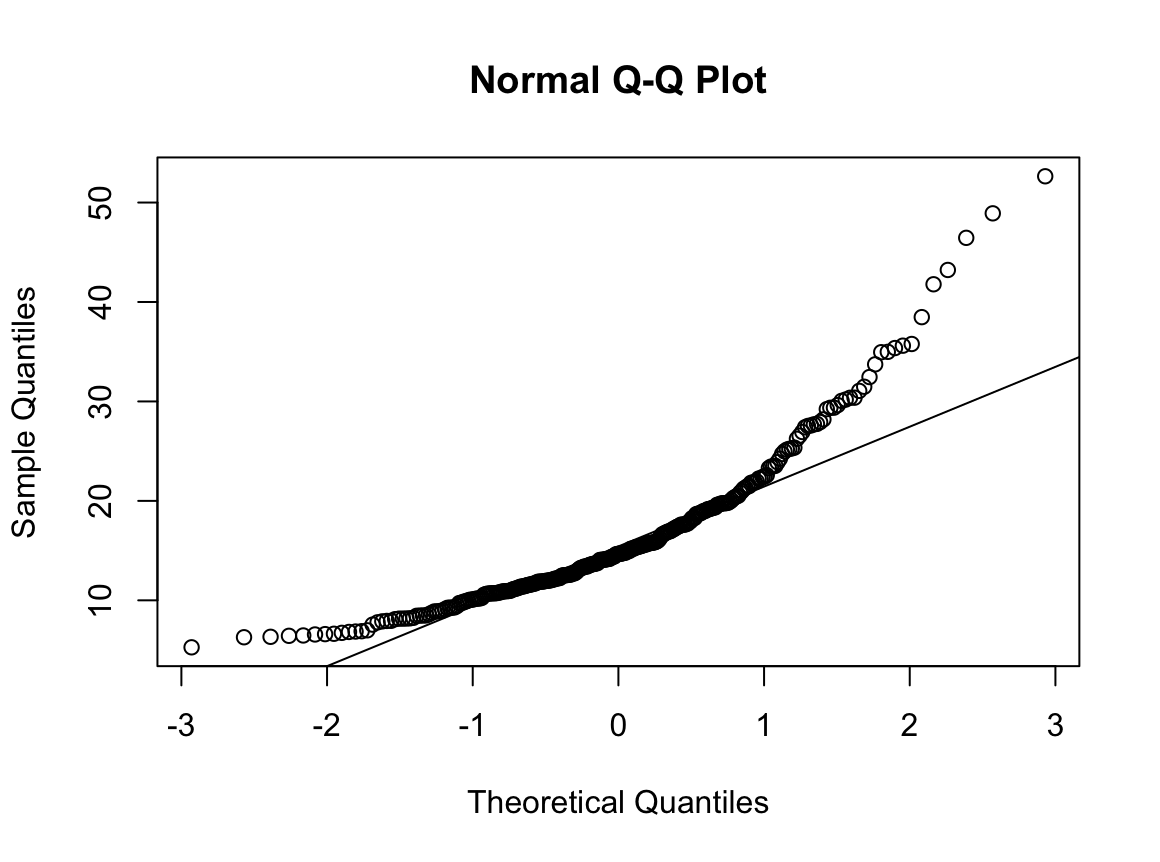
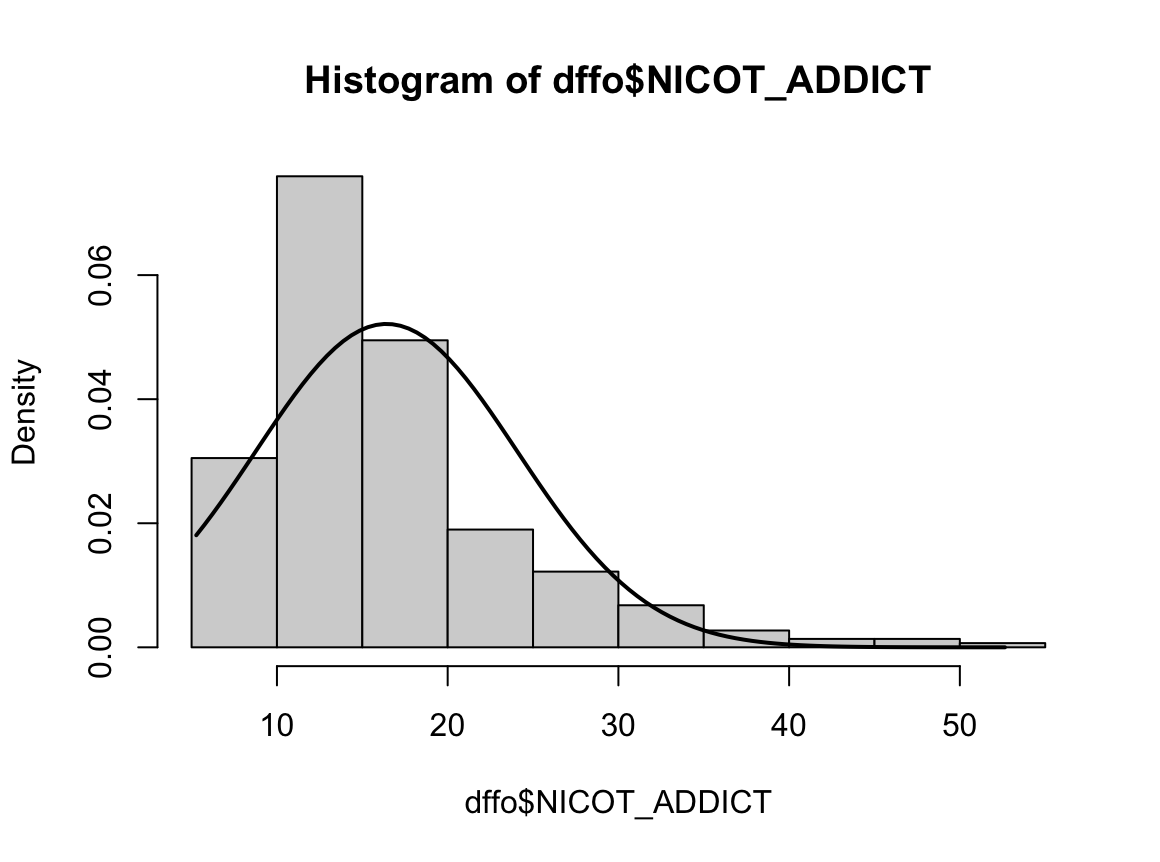
Shapiro-Wilk normality test
data: dffo$NICOT_ADDICT
W = 0.87644, p-value = 1.122e-14
3) 현재 흡연자
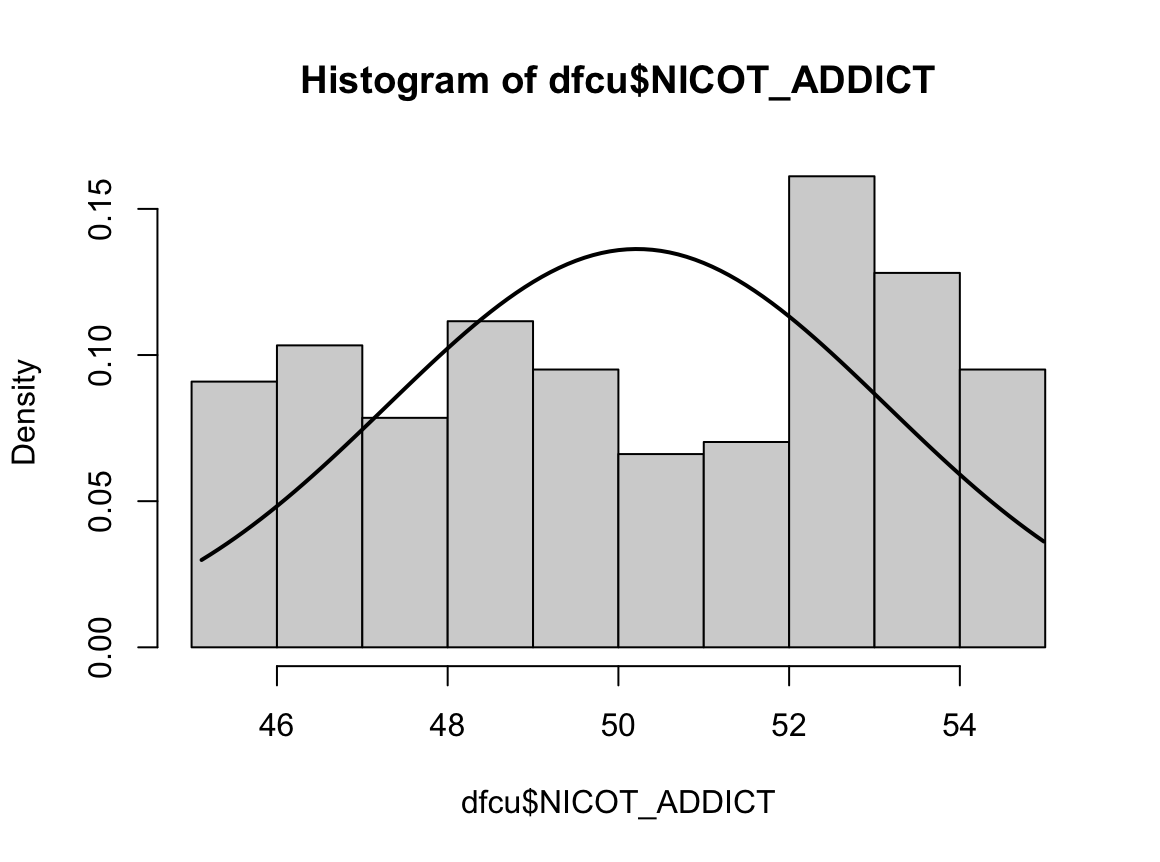
Shapiro-Wilk normality test
data: dfcu$NICOT_ADDICT
W = 0.93791, p-value = 1.364e-08N수가 2,000개 미만이므로 Shapiro-Wilk 통계량의 p-value를 보면 0.05 이하이며, Q-Q Plot은 대부분의 데이터가 선상에 있지 않고, 히스토그램에서도 정규성을 따르지 않는 것처럼 보인다. 따라서 일원 배치 분산 분석 (ANOVA)을 시행할 수 없고, 크루스칼 왈리스 분석 (Kruskal-Wallis Test)을 시행해야 한다.
지금까지 많은 분석을 할 때 분산이 같은지 여부 (등분산성)을 중요하게 여겼었다. 하지만 크루스칼 왈리스 분석은 분산이 달라도 어느 정도 괜찮다. 물론 분산에 아주 큰 차이가 나면 위험해지지만, 어느 정도는 robust 하므로 웬만하면 그냥 써도 괜찮다.
크루스칼 왈리스 (Kruskal Wallis) 검정 코드
kruskal.test(NICOT_ADDICT~SMOK, data=df)kruskal.test(NICOT_ADDICT~SMOK, data=df) : 데이터 df의 SMOK에 따라 NICOT_ADDICT의 중앙값에 차이가 있는지 Kruskal-Wallis 검정을 시행하라.
결과
Kruskal-Wallis rank sum test
data: NICOT_ADDICT by SMOK
Kruskal-Wallis chi-squared = 560.98, df = 2, p-value < 2.2e-16Kruskal-Wallis rank sum test
data: NICOT_ADDICT by SMOK
Kruskal-Wallis chi-squared = 560.98, df = 2, p-value < 2.2e-16
p-value가 0.05보다 작으므로 귀무가설을 기각하고 대립 가설을 채택한다. 그렇다면 여기에서 귀무가설 및 대립 가설은 무엇이었는가?
귀무가설: $H_0=$세 집단의 모집단 수준에서 중앙값은 "모두" 동일하다.
대립가설: $H_1=$ 세 집단의 모집단 수준에서 중앙값이 모두 동일한 것은 아니다.
우리는 대립 가설을 채택해야 하므로 "세 집단의 모집단 수준에서 중앙값이 모두 동일한 것은 아니다."라고 결론 내릴 것이다.
사후 분석
그런데, 세 집단의 중앙값이 모두 동일하지 않다는 말은 세 집단 중 두 개씩 골라 비교했을 때, 적어도 한 쌍에서는 차이가 난다는 것이다. 따라서 세 집단 중 두 개씩 골라 비교를 해보아야 하며, 이를 사후 분석 (post hoc analysis)이라고 한다. 세 집단에서 두 개씩 고르므로 가능한 경우의 수 $_3C_2=3$이다.
(1) 비흡연자 vs 과거 흡연자
(2) 비흡연자 vs 현재 흡연자
(3) 과거 흡연자 vs 현재 흡연자
비모수 검정인 Kruskal Wallis 검정의 사후 분석으로 쓰이는 방법은 다음 네 가지가 있다.
1) Pairwise Wilcoxon Test
2) Conover Test
3) Dunn Test
4) Nemenyi Test
코드
#1) Pairwise Wilcoxon Test
pairwise.wilcox.test(df$NICOT_ADDICT, df$SMOK, p.adjust.method="bonferroni", correct=FALSE)
#2) Conover Test
install.packages("DescTools")
library("DescTools")
ConoverTest(NICOT_ADDICT~SMOK, data=df)
#3) Dunn Test
DunnTest(NICOT_ADDICT~SMOK, data=df)
#4) Nemenyi Test
NemenyiTest(NICOT_ADDICT~SMOK, data=df)pairwise.wilcox.test(df$NICOT_ADDICT, df$SMOK, p.adjust.method="bonferroni", correct=FALSE) : df 데이터의 SMOK에 따라 df 데이터의 NICOT_ADDICT의 중앙값에 차이가 있는지 Wilcoxon rank sum test를 시행하는데, p-value의 보정은 Bonferroni 방법으로 시행하고, 연속성 수정은 하지 말아라. (연속성 수정에 관한 내용은 다음 링크를 확인하길 바란다.2022.08.30 - [통계 이론] - [이론] 연속성을 수정한 카이 제곱 검정 (Chi-squared test with Yates's correction for continuity))
ConoverTest(NICOT_ADDICT~SMOK, data=df) : df데이터의 SMOK에 따라 NICOT_ADDICT의 중앙값에 차이가 있는지 Conover test를 시행하라. Conover test, Dunn test, Nemenyi test모두 구조는 같다. 이 세 개의 함수는 "DescTools"라는 패키지에 포함되어 있으므로 설치를 먼저 해야 한다. 패키지 설치에 관한 내용은 다음 링크를 확인하길 바란다. 2022.08.05 - [통계 프로그램 사용 방법/R] - [R] 패키지 설치하기 - install.packages(), library()
결과
Pairwise comparisons using Wilcoxon rank sum test
data: df$NICOT_ADDICT and df$SMOK
0 1
1 8.3e-08 -
2 < 2e-16 < 2e-16
P value adjustment method: bonferroni
Conover's test of multiple comparisons : holm
mean.rank.diff pval
1-0 91.06188 2.6e-10 ***
2-0 532.38681 < 2e-16 ***
2-1 441.32493 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Dunn's test of multiple comparisons using rank sums : holm
mean.rank.diff pval
1-0 91.06188 2.3e-05 ***
2-0 532.38681 < 2e-16 ***
2-1 441.32493 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Nemenyi's test of multiple comparisons for independent samples (tukey)
mean.rank.diff pval
1-0 91.06188 6.9e-05 ***
2-0 532.38681 < 2e-16 ***
2-1 441.32493 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Pairwise comparisons using Wilcoxon rank sum test
data: df$NICOT_ADDICT and df$SMOK
0 1
1 8.3e-08 -
2 < 2e-16 < 2e-16
P value adjustment method: bonferroni
빨간색 글씨가 p-value를 의미하는데, 이는 다음과 같이 보면 된다.
| 0 | 1 | |
| 1 | 비흡연자 (0)와 과거 흡연자 (1) 비교 | |
| 2 | 비흡연자 (0)와 현재 흡연자 (2) 비교 | 과거 흡연자 (1)와 현재 흡연자 (2) 비교 |
모든 p-value가 0.05보다 작으므로 다음과 같이 결론 내릴 수 있다.
비흡연자 (0)와 과거 흡연자 (1) 사이에는 NICOT_ADDICT 중앙값에 차이가 있다.
비흡연자 (0)와 현재 흡연자 (2) 사이에는 NICOT_ADDICT 중앙값에 차이가 있다.
과거 흡연자 (1)와 현재 흡연자 (2)) 사이에는 NICOT_ADDICT 중앙값에 차이가 있다.
Conover's test of multiple comparisons : holm
mean.rank.diff pval
1-0 91.06188 2.6e-10 ***
2-0 532.38681 < 2e-16 ***
2-1 441.32493 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Dunn's test of multiple comparisons using rank sums : holm
mean.rank.diff pval
1-0 91.06188 2.3e-05 ***
2-0 532.38681 < 2e-16 ***
2-1 441.32493 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Nemenyi's test of multiple comparisons for independent samples (tukey)
mean.rank.diff pval
1-0 91.06188 6.9e-05 ***
2-0 532.38681 < 2e-16 ***
2-1 441.32493 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Conover Test, Dunn Test, Nemenyi Test 결과를 보는 방법은 같다.
| 1-0 | 비흡연자 (0)와 과거 흡연자 (1) 비교 |
| 2-0 | 비흡연자 (0)와 현재 흡연자 (2) 비교 |
| 1-2 | 과거 흡연자 (1)와 현재 흡연자 (2) 비교 |
모든 p-value가 0.05보다 작으므로 다음과 같이 결론 내릴 수 있다.
비흡연자 (0)와 과거 흡연자 (1) 사이에는 NICOT_ADDICT 중앙값에 차이가 있다.
비흡연자 (0)와 현재 흡연자 (2) 사이에는 NICOT_ADDICT 중앙값에 차이가 있다.
과거 흡연자 (1)와 현재 흡연자 (2)) 사이에는 NICOT_ADDICT 중앙값에 차이가 있다.
즉, 어떤 방법을 사용하더라도 유의미하게 나온다.
하지만, 위 분석 방법들은 서로 다른 모양의 분포, 서로 다른 분산에 대한 고려가 부족하므로, 필자는 여기에 아직 쓰이고 있지는 않지만 한 가지 방법을 추가로 제안한다. 바로, Robust rank order test의 p-value를 보정하여 쓰는 것이다. (Robust rank order test에 대한 내용은 다음 링크를 확인하길 바란다.2022.12.01 - [모평균 검정/R] - [R] 로버스트 순위 순서 검정 (비모수 독립 표본 중앙값 검정: Robust rank order test, Flinger-Pollicello test) - rrod.test())
rrod1<-rrod.test(dfne$NICOT_ADDICT, dffo$NICOT_ADDICT)
rrod2<-rrod.test(dfne$NICOT_ADDICT, dfcu$NICOT_ADDICT)
rrod3<-rrod.test(dffo$NICOT_ADDICT, dfcu$NICOT_ADDICT)
p1<-rrod1$p.value
p2<-rrod2$p.value
p3<-rrod3$p.value
p<-c(p1, p2, p3)
p.adjust(p, "bonferroni")
p.adjust(p, "fdr")각각의 pairwise로 robust rank order test를 시행하고, 각각의 p-value를 모아 보정을 하는 것이다.
p<-c(p1, p2, p3) : p1, p2, p3을 묶어 하나의 p에 저장하라
p.adjust(p, "bonferroni") : p에 있는 값들을 보정하되, bonferroni adjustment를 사용하라.
Bonferroni 외에도, holm, hochberg, hommel, BH, BY, fdr을 넣어 각각의 방법으로 보정을 시도할 수 있다.
어떤 사후 분석을 쓸 것인가
이 논의에 대해 정답이 따로 있는 것은 아니다. 적절한 방법을 사용하여 논문에 제시하면 되고, 어떤 것이 정답이라고 콕 집어 이야기할 수는 없다. 다만, 사후 분석 방법이 여러 가지가 있다는 것은 '사후 분석 방법에 따라 산출되는 결과가 달라질 수 있다.'는 것을 의미하고, 심지어는 '어떤 사후 분석 방법을 채택하냐에 따라 유의성 여부가 달라질 수도 있다.'는 것을 의미한다. 심지어, Kruskal-Wallis test에서는 유의한 결과가 나왔는데, 사후 분석을 해보니 유의한 차이를 보이는 경우가 없을 수도 있다. 따라서 어떤 사후 분석 방법 결과에 따른 결과인지 유의하여 해석할 필요가 있다.
왜 굳이 Kruskal Wallis test를 쓰는 것인가?
이 시점에서 이런 의문이 들 수 있다.
"각각의 그룹별로 평균을 비교하면 되지, 굳이 왜 Kruskal Wallis test라는 방법까지 사용하는 것인가?"
아주 논리적인 의문점이다. 하지만, 반드시 Kruskal-Wallis test를 사용해야 한다. 그 이유는 다음과 같다. 본 사례는 흡연 상태에 따른 조합 가능한 경우의 수가 3인데, 각각 유의성의 기준을 $\alpha=0.05$로 잡아보자. 이때 세 번의 비교에서 모두 귀무가설이 학문적인 진실인데(평균에 차이가 없다.), 세 번 모두 귀무가설을 선택할 확률은 $\left( 1-0.05 \right)^3 \approx 0.86$이다. (이해가 어려우면 p-value에 대한 설명 글을 읽고 오길 바란다. 2022.09.05 - [통계 이론] - [이론] p-value에 관한 고찰)
그런데, Kruskal-Wallis test의 귀무가설은 "모든 집단의 중앙값이 같다."이다. 따라서 모든 집단의 중앙값이 같은 것이 학문적 진실일 때, 적어도 한 번이라도 대립 가설을 선택하게 될 확률은 $1-0.86=0.14$가 된다. 즉, 유의성의 기준이 올라가게 되어, 덜 보수적인 결정을 내리게 되고, 다시 말하면 대립 가설을 잘 선택하는 쪽으로 편향되게 된다. 학문적으로는 '다중 검정 (multiple testing)을 시행하면 1종 오류가 발생할 확률이 증가하게 된다.'라고 표현한다.
따라서, 각각을 비교해보는 것이 아니라 한꺼번에 비교하는 Kruskal-Wallis test를 시행해야 함이 마땅하다.
여기에서 한 번 더 의문이 들 수 있다.
"사후 분석을 할 때에는 1종 오류가 발생하지 않는가?"
그렇다. 1종 오류가 발생할 확률이 있으므로, p-value의 기준을 더 엄격하게 (0.05보다 더 작게) 잡아야 한다. P-value를 보정하는 방법은 일반적으로는 Bonferroni, holm, hochberg, hommel, BH, BY, FDR 등이 있고, Kruskal-Wallis test의 사후 분석 방법으로는 특별히 Pairwise Wilcoxon Test, Conover Test, Dunn Test, Nemenyi Test을 사용하고 있다.
코드 정리
##워킹 디렉토리 지정
setwd("C:/Users/user/Documents/Tistory_blog")
##데이터 불러오기
install.packages("readr")
library("readr")
df<-read_csv("Data.csv")
##데이터 나누기
dfne<-df[df$SMOK==0,]
dffo<-df[df$SMOK==1,]
dfcu<-df[df$SMOK==2,]
##정규성 검정
#비흡연자
# 1) Q-Q plot 그리기
qqnorm(dfne$NICOT_ADDICT)
qqline(dfne$NICOT_ADDICT)
# 2) 히스토그램 그리기
hist(dfne$NICOT_ADDICT, prob=TRUE)
NICOT_ADDICTrange<-seq(min(dfne$NICOT_ADDICT),max(dfne$NICOT_ADDICT),length=max(max(dfne$NICOT_ADDICT)-min(dfne$NICOT_ADDICT),100))
ND<-dnorm(NICOT_ADDICTrange,mean=mean(dfne$NICOT_ADDICT),sd=sd(dfne$NICOT_ADDICT))
lines(NICOT_ADDICTrange, ND, lwd=2)
# 3) Shapiro-Wilk test 시행하기
shapiro.test(dfne$NICOT_ADDICT)
#과거 흡연자
# 1) Q-Q plot 그리기
qqnorm(dffo$NICOT_ADDICT)
qqline(dffo$NICOT_ADDICT)
# 2) 히스토그램 그리기
hist(dffo$NICOT_ADDICT, prob=TRUE)
NICOT_ADDICTrange<-seq(min(dffo$NICOT_ADDICT),max(dffo$NICOT_ADDICT),length=max(max(dffo$NICOT_ADDICT)-min(dffo$NICOT_ADDICT),100))
ND<-dnorm(NICOT_ADDICTrange,mean=mean(dffo$NICOT_ADDICT),sd=sd(dffo$NICOT_ADDICT))
lines(NICOT_ADDICTrange, ND, lwd=2)
# 3) Shapiro-Wilk test 시행하기
shapiro.test(dffo$NICOT_ADDICT)
#현재 흡연자
# 1) Q-Q plot 그리기
qqnorm(dfcu$NICOT_ADDICT)
qqline(dfcu$NICOT_ADDICT)
# 2) 히스토그램 그리기
hist(dfcu$NICOT_ADDICT, prob=TRUE)
NICOT_ADDICTrange<-seq(min(dfcu$NICOT_ADDICT),max(dfcu$NICOT_ADDICT),length=max(max(dfcu$NICOT_ADDICT)-min(dfcu$NICOT_ADDICT),100))
ND<-dnorm(NICOT_ADDICTrange,mean=mean(dfcu$NICOT_ADDICT),sd=sd(dfcu$NICOT_ADDICT))
lines(NICOT_ADDICTrange, ND, lwd=2)
# 3) Shapiro-Wilk test 시행하기
shapiro.test(dfcu$NICOT_ADDICT)
##Kruskal Wallis Test
kruskal.test(NICOT_ADDICT~SMOK, data=df)
##Post hoc analysis
#1) Pairwise Wilcoxon Test
pairwise.wilcox.test(df$NICOT_ADDICT, df$SMOK, p.adjust.method="bonferroni", correct=FALSE)
#2) Conover Test
install.packages("DescTools")
library("DescTools")
ConoverTest(NICOT_ADDICT~SMOK, data=df)
#3) Dunn Test
DunnTest(NICOT_ADDICT~SMOK, data=df)
#4) Nemenyi Test
NemenyiTest(NICOT_ADDICT~SMOK, data=df)
#5) Pairwise robust rank order test
rrod1<-rrod.test(dfne$NICOT_ADDICT, dffo$NICOT_ADDICT)
rrod2<-rrod.test(dfne$NICOT_ADDICT, dfcu$NICOT_ADDICT)
rrod3<-rrod.test(dffo$NICOT_ADDICT, dfcu$NICOT_ADDICT)
p1<-rrod1$p.value
p2<-rrod2$p.value
p3<-rrod3$p.value
p<-c(p1, p2, p3)
p.adjust(p, "bonferroni")
p.adjust(p, "fdr")
[R] 크루스칼 왈리스 검정 (비모수 일원 배치 분산 분석: Kruskal-Wallis Test) 정복 완료!
작성일: 2022.12.01.
최종 수정일: 2022.12.01.
이용 프로그램: R 4.2.2
RStudio v2022.07.2
RStudio 2022.07.2+576 "Spotted Wakerobin" Release
운영체제: Windows 10, Mac OS 12.6.1