[SAS] 다중 선형 회귀 분석 (Multiple linear regression) - PROC REG, PROC GLM
지난 포스팅에서 연속형 변수의 단순 선형 회귀 분석 (Simple linear regression: 2023.05.14 - [선형 회귀 분석/SAS] - [SAS] 단순 선형 회귀 분석 (Simple linear regression) - PROC REG), 범주형 변수의 단순 선형 회귀 분석 (Simple linear regression with categorical variables: 2023.10.19 - [선형 회귀 분석/SAS] - [SAS] 범주형 변수의 선형 회귀 분석 (Simple linear regression with categorical variable) - PROC REG, PROC GLM)에 대해 알아보았다. 위 분석들은 모두 독립 변수가 1개인 단순 선형 회귀 분석이다. 하지만 세상 일은 그렇게 단순하지 않다.
교란 변수 (Confounder, confounding variable)
우리는 앞서 연속형 변수의 단순 선형 회귀 분석 (Simple linear regression: 2023.05.14 - [선형 회귀 분석/SAS] - [SAS] 단순 선형 회귀 분석 (Simple linear regression) - PROC REG) 포스팅에서 수축기 혈압과 심혈관 질환의 관련성을 찾아보았다. 그런데, 비만인 사람은 혈압이 대체적으로 높은 것으로 알려져 있다. 더구나 비만인 사람은 심혈관 질환의 위험도도 높아지는 것으로 알려져 있다. 그렇다면, "수축기 혈압이 높았던 사람에게서 높은 심혈관 질환 위험 점수가 발견되었던 것은 그냥 그 사람이 비만도가 높아 당연히 수축기 혈압도 높고, 심혈관 질환 위험 점수도 높았던 것이 아닐까?"라는 의문이 든다. 즉, "우리가 이전 단순 선형 회귀 분석에서 발견한 과학적 현상(수축기 혈압이 높으면 심혈관 질환 위험 점수가 높아진다.)은 사실은 비만 때문이 아니었을까?"라는 의문이 들게 된다. 이렇게 독립변수와 종속변수 모두의 원인이 되는 변수를 교란 변수라고 하며, 이런 현상(교란)은 통계 분석을 할 때 반드시 교정을 해야 한다. (사실 독립변수는 인과적 관계가 아니라 연관 관계이기만 해도 충분하다.)
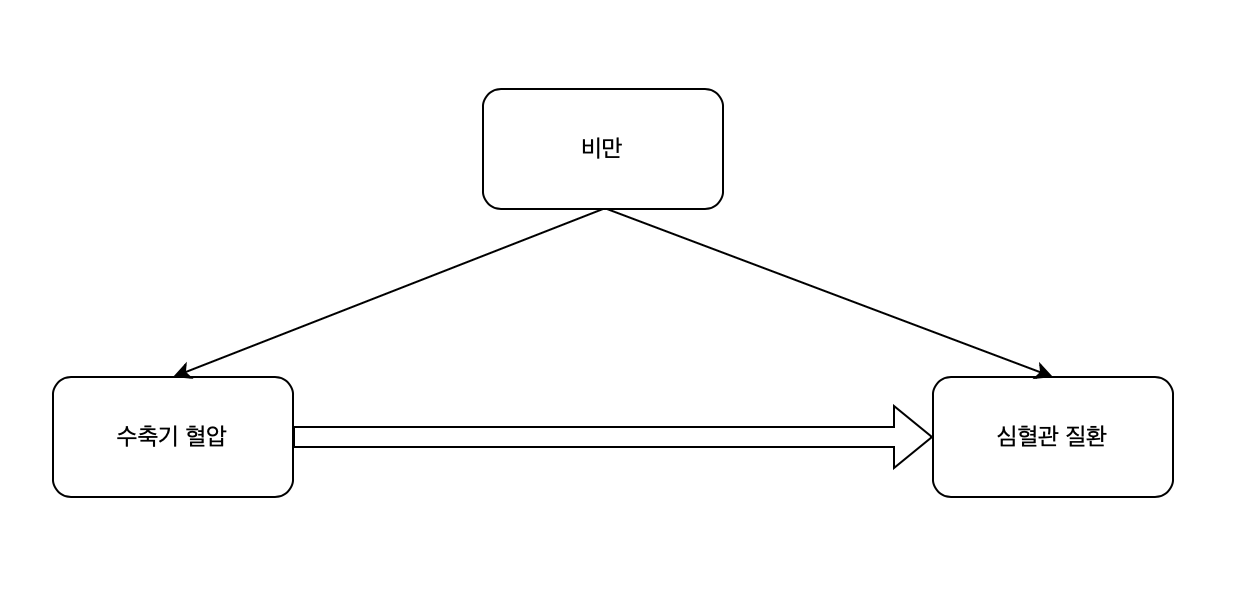
교란 현상의 해결 방법: 다중 회귀 분석
교란 현상을 해결하는 방법은 보정(adjustment)과 층화(stratification)가 있다. 층화도 좋은 방법이고, 때로는 보정을 할 수 없어 층화를 해야만 할 때도 있지만, 보통 표본의 수가 부족해지는 문제가 있기 때문에, 층화가 아니라 보정을 시행하곤 한다. 보정을 시행할 수 있는 방법으로는 이전에 다룬 편상관 분석(2023.04.20 - [상관분석/SAS] - [SAS] 편상관 계수, 부분 상관 계수 (Partial correlation coefficient) - PROC CORR)이 있다. 하지만 이는 상관 계수만 구할 수 있어 "예측할 수 있는 정도"만 표현할 수 있다. 그 대신 비만도의 영향을 보정했을 때, 수축기 혈압이 1 단위 증가할 때 심혈관 질환 위험 점수가 얼마나 증가하는지(기울기)를 알 수 있는 방법으로는 본 포스팅에서 다룰 다중 선형 회귀 분석이 있다.
*실습용 데이터는 아래 링크를 클릭하면 다운로드할 수 있습니다.
2022.08.04 - [공지사항 및 소개] - 분석용 데이터 (update 22.12.18)
분석용 데이터 (update 22.12.18)
2022년 12월 18일 버전입니다. 변수는 계속하여 추가될 예정입니다. 다음 카테고리에 있는 글에서 이용된 데이터입니다. - 기술 통계 - 범주형 자료 분석 - 모평균 검정 - 상관분석 - 반복 측정 자료
medistat.tistory.com
시작하기 위해 라이브러리를 만들고, 파일을 불러온다.
라이브러리 만드는 방법: 2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 라이브러리 만들기 - LIBNAME
파일 불러오는 방법: 2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 데이터 불러오기 및 저장하기 - PROC IMPORT, PROC EXPORT
*라이브러리 지정하기;
LIBNAME hong "C:/Users/User/Documents/Tistory_blog";
*파일 불러오기;
PROC IMPORT
DATAFILE="C:\Users\user\Documents\Tistory_blog\Data.xlsx"
DBMS=EXCEL
OUT=hong.df
REPLACE;
RUN;
목표: BMI의 영향을 배제 혹은 교정했을 때 수축기 혈압(SBP)이 1 단위 증가할 때 심혈관 질환 위험 점수(CVD_RISK)는 얼마나 증가하는가?
단순 선형 회귀 분석과 같이 PROC REG 명령어를 사용하며, 코드는 다음과 같다.
코드
PROC REG DATA=hong.df;
MODEL CVD_RISK=SBP BMI;
RUN;PROC REG DATA=hong.df; : 선형 회귀분석을 시작하라. 데이터는 hong 라이브러리에 있는 df를 사용하라.
독립변수에 사용된 SBP, BMI 모두 연속변수이기에 PROC GLM이 아니라 REG를 사용해도 무방하다.
MODEL CVD_RISK=SBP BMI; : 종속 변수는 CVD_RISK로, 독립 변수에는 SBP와 BMI를 사용하라. SBP와 BMI의 순서가 바뀌는 것은 아무 상관이 없다. 즉, BMI를 보정했을 때의 SBP의 영향과 SBP를 보정했을 때의 BMI의 영향을 동시에 파악하는 것이다.
결과
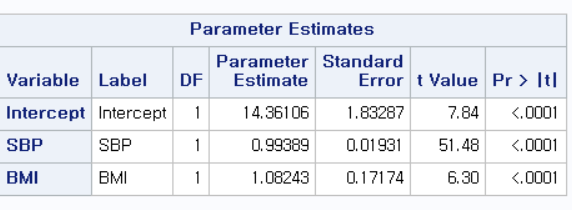
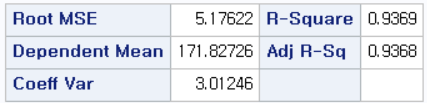
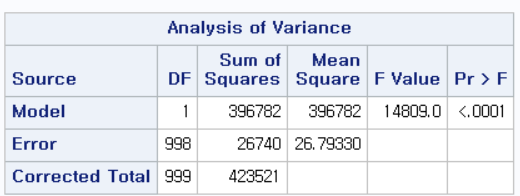
해석의 방법은 단순 선형 회귀 분석에서와 같다. (2023.05.14 - [선형 회귀 분석/SAS] - [SAS] 단순 선형 회귀 분석 (Simple linear regression) - PROC REG) 그리고, Analysis of Variance Table, Root MSE, R-Square, Dependent Mean, Adj R-Sq, Coeff Var에 대한 내용도 위 단순 선형 회귀 분석 링크에서 확인할 수 있다.
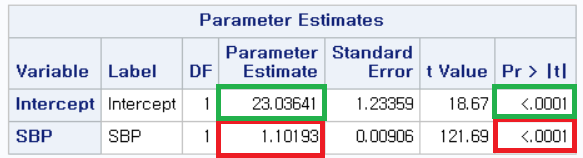
BMI의 영향을 보정하더라도, SBP가 1 단위 증가할 때 CVD_RISK는 0.99389만큼 증가하며 이에 대한 p-value는 0.0001보다 작아 매우 유의함을 알 수 있다.
또한, SBP의 영향을 보정하더라도, BMI가 1 단위 증가할 때 CVD_RISK는 1.08243만큼 증가하며 이에 대한 p-value는 0.0001보다 작아 매우 유의함을 알 수 있다.
즉, 단순 회귀 분석에서 나타난 수축기 혈압과 심혈관 질환 위험 점수 사이의 유의한 관련성은 BMI의 영향을 보정하더라도 유의함을 알 수 있다. 또한, 단순 회귀 분석에서의 회귀 계수 1.10193보다 작으므로, 일부분의 설명력은 BMI에게 빼았겼음을 알 수 있다.
보정 변수가 두 개 이상일 때 코드
BMI 외에 흡연 상태로도 보정하고 싶을 수 있다. 이럴 땐 어떻게 해야 할까? 답은, 단순히 BMI 뒤에 추가적인 보정변수를 띄어쓰기를 이용하여 나열하면 된다. 그런데, 선형 회귀 분석 전에 연속형 변수와 범주형 변수의 전처리가 다르다는 것을 일전에 소개한 적이 있다. 범주형 변수는 분석 전에 범주형 자료임을 SAS에게 알려주어야 한다. 내용은 다음 링크를 확인하면 된다.
연속형 변수: 2023.05.14 - [선형 회귀 분석/SAS] - [SAS] 단순 선형 회귀 분석 (Simple linear regression) - PROC REG
그런데, 흡연 상태 (SMOK)는 범주형 자료다. 따라서 선형 회귀 분석을 시행하기 전에 범주형임을 알려주어야 한다.
PROC GLM DATA=hong.df;
CLASS SMOK(REF='0');
MODEL CVD_RISK= SBP BMI SMOK/SOLUTION;
RUN;
QUIT;PROC GLM DATA=hong.df; : 선형 회귀분석을 시작하라. 데이터는 hong 라이브러리에 있는 df를 사용하라.
독립변수에 사용된 SMOK가 범주형 변수이기에 PROC REG이 아니라 GLM를 사용해야만 한다.
CLASS SMOK(REF='0'); : SMOK는 범주형 자료다. 참고치는 0으로 한다.
MODEL CVD_RISK= SBP BMI SMOK/SOLUTION; : 결과변수는 CVD_RISK, 독립변수는 SBP, BMI, SMOK이다. 각 변수에 대한 beta값, 표준오차, p-value 등을 산출하라. (SOLUTION)
RUN; : 실행하라.
QUIT; : GLM을 종료하라. (QUIT이 필요하지 않은 다른 구문을 추가로 시행해도 상관없다.)
결과
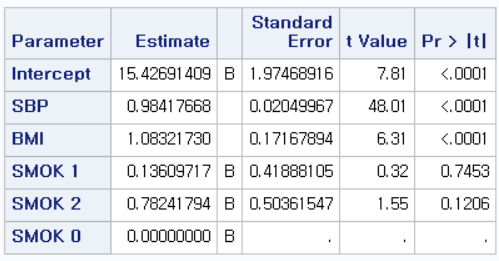
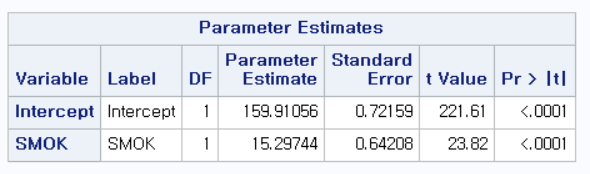
SBP, BMI는 유의한 결과를 보이고 있지만, SMOK는 1(과거 흡연자), 2(현재 흡연자) 모두 유의한 결과를 보이고 있지 않다.
"BMI와 흡연 상태로 보정을 하였을 때, 수축기 혈압 1 단위 증가할 때, CVD_RISK는 0.98417668점 증가한다"라고 할 수 있지만
"SBP와 BMI로 보정을 하였을 때, 비흡연자와 과거 흡연자 혹은 비흡연자와 현재 흡연자 사이의 CVD_RISK의 차이는 존재하지만 유의하다고 할 수 없다."라고 결론 내리게 된다.
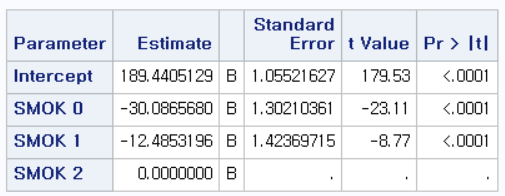
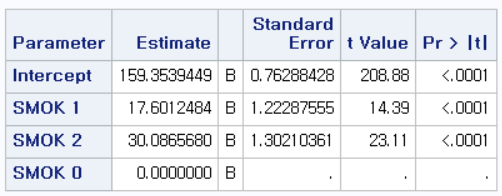
또한 중요한 것은, 만약 SMOK를 단순히 보정변수로만 보고 CVD_RISK와 SBP 사이의 관계만 확인하고 싶다면, SMOK의 참고치(REF)를 무엇으로 설정하든 같은 결과를 낸다는 것이다. 따라서 주된 독립변수가 아니라면 REF를 무엇으로 잡을지 크게 신경 쓰지 않아도 될 뿐만 아니라, 따로 지정을 하지 않아도 상관없다.
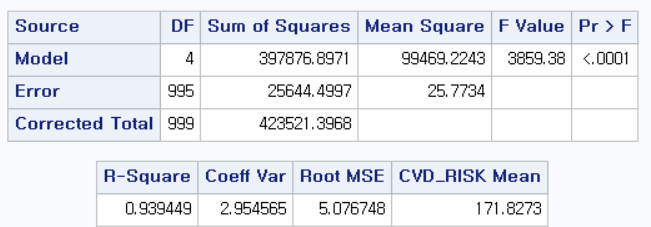
위 두 개의 표는 다음 링크에서 내용을 확인하길 바란다. (2023.05.14 - [선형 회귀 분석/SAS] - [SAS] 단순 선형 회귀 분석 (Simple linear regression) - PROC REG) CVD_RISK Mean 은 위 링크에서 "Dependent Mean"에 해당한다.
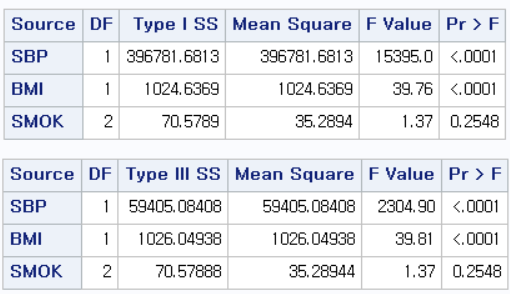
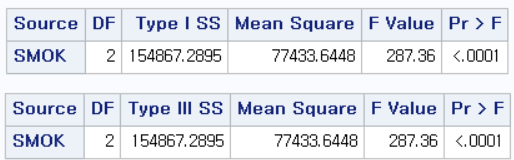
위 두 개의 표 SS(Sum of Squares)에 관한 것인데, Type I과 Type III가 있다. 이는 다음 링크에서 내용을 확인하길 바란다. (링크 추가 예정)
코드 정리
*라이브러리 지정하기;
LIBNAME hong "C:/Users/User/Documents/Tistory_blog";
*파일 불러오기;
PROC IMPORT
DATAFILE="C:\Users\user\Documents\Tistory_blog\Data.xlsx"
DBMS=EXCEL
OUT=hong.df
REPLACE;
RUN;
*다중 선형 회귀분석 시행;
PROC REG DATA=hong.df;
MODEL CVD_RISK=SBP BMI;
RUN;
PROC GLM DATA=hong.df;
CLASS SMOK(REF='0');
MODEL CVD_RISK= SBP BMI SMOK/SOLUTION;
RUN;
QUIT;
[SAS] 다중 선형 회귀 분석 (Multiple linear regression) 정복 완료!
작성일: 2023.10.22.
최종 수정일: 2023.10.23.
이용 프로그램: SAS v9.4
운영체제: Windows 11
'선형 회귀 분석 > SAS' 카테고리의 다른 글
| [SAS] 범주형 변수의 선형 회귀 분석 (Simple linear regression with categorical variable) - PROC REG, PROC GLM (1) | 2023.10.19 |
|---|---|
| [SAS] 선형 회귀 분석의 전제 조건 - PROC REG (1) | 2023.10.17 |
| [SAS] 단순 선형 회귀 분석 (Simple linear regression) - PROC REG (0) | 2023.05.14 |