
[이론] 가우스-마르코프 정리 (Gauss-Markov Theorem)
이전 최소제곱법 글(2023.06.15 - [통계 이론] - [이론] 보통최소제곱법 (Ordinary Least Squares))에서 회귀 계수를 구하는 방법에 대해 알아보았다. 가우스-마르코프 정리는, 최소제곱법에서 추정한 회귀 계수 값들이 특정한 조건 하에서 가장 좋은 추정량이 된다는 정리다. 그 조건들은 다음과 같다.
(1) 선형성 (Linearity) : Linearity in parameters
회귀계수가 선형이어야 한다. 즉, $Y=aX+b$와 같은 관계여야 한다. 여기에서 중요한 것은 a지 X가 아니다. a가 선형이어야 하지, X는 선형이 아니어도 된다. 즉, $Y=aX^2+b$와 같은 관계도 선형이다. 심지어 $Y=af(X)+b$도 회귀계수에 대해서는 선형이다.
(2) 독립변수의 비확률성(Nonstochasticity) : Nonstochasticity of regressors (independent variables)
독립변수는 미리 정해져 있어야 한다. 즉, 독립변수는 확률변수면 안 된다. 풀어 말하면, 독립변수의 값이 구해져 있는 상태에서 종속변수의 값을 측정해야 한다. 하지만, 일반적인 연구를 할 때에는 독립변수와 종속변수를 동시에 측정한다. 즉, 독립변수가 미리 정해져 있지 않고, 달리 말하면 확률변수라고 말할 수 있다. 이런 경우에는 다음과 같은 조건으로 조금 완화하기도 한다. "독립변수의 값과 잔차의 값은 관련이 없어야 한다."
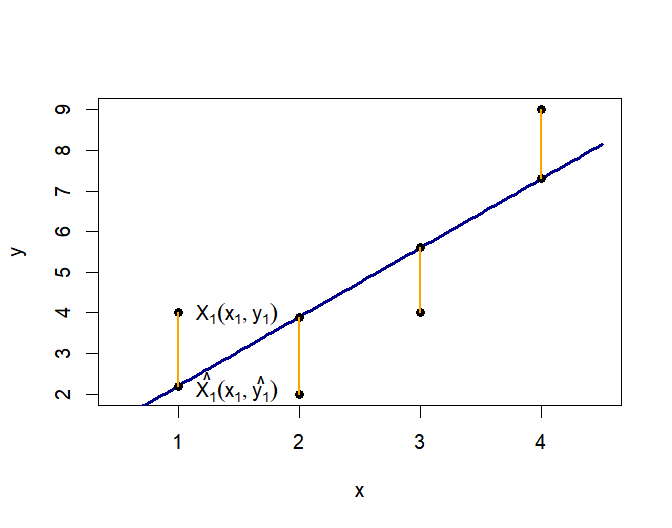
위 그림에서 $x_i$값과 오렌지색 선분의 길이는 상관이 없어야 한다. 만약, $x_i$값이 커짐에 따라 오렌지색 선분의 길이가 길어진다면 그것은 관련이 있다는 뜻이다. 예를 들어, 나이와 지식수준의 관련성을 확인하는 상황을 생각해 보면, 3살짜리 아이들의 지식수준은 비슷비슷한데(오렌지색 선분이 짧음), 성인의 차이가 많이 나므로 비상관성이 성립하지 않을 수 있다. (이는 표준화 등의 방법으로 해결할 수 있긴 하다.)
(3) 오차의 평균=0
관측치들은 회귀선 위에도, 아래에도 고르게 분포하여 오차의 평균은 0이 되어야 한다.
$$ \forall_i, E \left( \epsilon_j | x_i \right)=0$$
즉, 독립변수가 특정 값인 관측치들만 따로 뽑아 종속변수의 평균을 구하면 회귀선 위에 위치한다는 뜻이다.
$$ \forall_i, E\left(y_j | x_i \right) = \alpha + \beta x_i $$
(4) 등분산성 (Homoscedasticity): 오차의 등분산성
대표적인 대푯값으로는 평균과 표준편차가 있다. 오차의 평균은 위에서 다루었으니, 표준편차도 다루어보도록 한다. 표준편차의 제곱이 분산이므로 표준편차를 다루는 것은 분산을 다루는 것과 같다.
독립변수의 값에 관계없이, 종속변수가 퍼져있는 정도는 비슷해야 한다. 즉, 오차가 퍼져있는 정도는 독립변수의 값에 관계없이 일정해야 한다. 따라서 적절한 상수 $\sigma$에 대해 다음 수식이 성립해야 한다. 그리고, $\sigma$를 표준편차라 한다.
$$\forall_i, var \left( \epsilon_j | x_i \right) = \sigma^2 $$
만약 등분산성이 성립하지 않는다면, 즉 $var \left( \epsilon_j | x_i \right)=\sigma_i ^2$이라면, 이분산성 (heteroscedasticity)을 보인다고 한다.
(5) 비자기상관성 (Nonautocorrelation)
한 오차로 다른 오차값을 예상할 수 있으면 안 된다. 각 개인이 10살일 때, 20살일 때의 키에 대한 데이터가 있다고 하자. 10살일 때 키가 평균보다 컸던 사람(오차가 큰 사람)은 20살일 때에도 클(오차가 클) 확률이 높다. 즉, 한 오차값을 알면 다른 오차값을 예측할 수 있게 된다. 이런 경우 자기상관(autocorrelation)이 있다고 하며, 이런 경우는 적절하지 않다. 이를 수식으로 표현하면 다음과 같다.
$$\forall_{i,k}, cov\left(\epsilon_j, \epsilon_l | x_i , x_k \right)=0$$
(6) 다중공선성 없음 (No multicollinearity)
마지막으로, 다중공선성이 없어야 한다. 보통 다중공선성은 공선성의 개념을 포함하는 것처럼 통용되므로, 본 글에서 다중공선성이 없다는 것은, 공선성도 없다는 것을 내포하기로 한다. 먼저, 공선성과 다중공선성에 대해서 알아보기로 한다.
공선성이란 "모델에 있는 두 독립변수 간에 긴밀한 상관관계가 있는 것"으로 정의할 수 있다. 예를 들어, 종속변수가 "삶의 질"일 때, 독립변수로 "월 수입"과 "연 수입" 두 개를 넣는 상황을 상정해 보자. 이때, "연 수입 = 월 수입 * 12"라는 정확한 상관관계가 존재하므로, 공선성이 존재한다고 할 수 있고, 두 개의 변수를 모델에 모두 넣으면 안 된다.
다중공선성이란 "모델에 있는 세 개 이상의 독립변수 간에 일종의 선형 관계가 있는 것"으로 정의할 수 있다. 예를 들어, 독립변수로 "출생 연도", "나이", "현재 년도" 세 가지를 쓰는 상황을 생각해 보자. 이때 "나이=현재 년도 - 출생 연도"라는 정확한 선형 관계가 존재하므로, 다중공선성이 존재한다고 할 수 있다. 따라서 이 세 변수를 모두 독립변수로 사용하려 하면 안 된다. (이런 경우에 세 변수를 모두 독립변수로 사용하기 위한 방법으로 Age-Period-Cohort Analysis가 존재하고, 이 다중공선성을 해결하기 위해 여러 방법론들이 제시되었다. 다음 링크에서 내용을 확인할 수 있다. 링크 추가 예정)
여기까지가 가우스 마르코프 정리의 내용이다. 통계 공부를 좀 해보신 분들이라면 알 수 있겠지만, 이는 선형 회귀 분석의 가정으로 이어진다. 그리고 이런 모델을 Classical Linear Regression Model이라고 한다.
SPSS : 링크 추가 예정
SAS : 링크 추가 예정
R: 2022.12.22 - [선형 회귀 분석/R] - [R] 선형 회귀 분석의 전제 조건 - lm(), plot(), gvlma()
여기서 의문이 든다. 그렇다면 왜 선형 회귀 분석의 전제조건으로 "잔차의 정규성"을 요구할까?
이는 가설 검정을 통해 유의성, 즉 p-value를 산출하기 위함이다. 정확히 말하면, 잔차의 정규성을 만족하는 순간, 보통 최소 제곱법은 최대가능도와 같은 것이 되므로, 최소제곱법 대신 최대가능도 방법을 사용할 수 있다. 각각에 대한 내용은 다음 링크를 확인하길 바란다.
최소제곱법: 2023.06.15 - [통계 이론] - [이론] 보통최소제곱법 (Ordinary Least Squares)
최대가능도: 2022.11.25 - [통계 이론] - [이론] 로지스틱 회귀분석에서 회귀 계수를 구하는 방법 - Maximum likelihood estimation
그리고, 잔차의 정규성까지 만족하는 모델을 Classical Normal Linear Regression Model이라고 한다.
[이론] 가우스-마르코프 정리 (Gauss-Markov Theorem) 정복 완료!
작성일: 2023.06.21.
최종 수정일: 2023.06.21.
'통계 이론' 카테고리의 다른 글
| [이론] 보통최소제곱법 (Ordinary Least Squares) (0) | 2023.06.15 |
|---|---|
| [이론] 로지스틱 회귀분석에서 회귀 계수를 구하는 방법 - Maximum likelihood estimation (0) | 2022.11.25 |
| [이론] 콕스 회귀 모델에서 생존 함수의 표현 (0) | 2022.11.10 |
| [이론] 생존 함수와 위험 함수의 관계 (0) | 2022.11.10 |
| [이론] p-value에 관한 고찰 (0) | 2022.09.05 |