
[R] 선형 회귀 분석의 전제 조건 - lm(), plot(), gvlma()
지난 포스팅에서 단순 선형 회귀 분석을 소개하며, 전제 조건(가정)에 대한 논의가 필요하다고 했다. (단순 선형 회귀 분석:2022.12.22 - [선형 회귀 분석/R] - [R] 단순 선형 회귀 분석 (Simple linear regression) - lm()) 보통 네 가지 전제조건을 의미하며, 그중 통계적으로 검정하는 조건은 세 가지다.
1) 정규성(Normality) : 잔차의 정규성
2) 선형성(Linearity) : 독립변수와 종속변수의 선형성
3) 잔차의 등분산성 (Homoscedasticity) : 잔차의 분산은 종속변수의 값에 따라 달라지지 않는다.
4) 독립성 (Independence): 관측 간의 독립성
이 중 4번 "독립성"은 통계적으로 검정하진 않는다. 독립성이란 개별 관측 간에는 연관되어있지 않다는 뜻이다. 대표적인 사례가 반복 측정이다. 같은 사람에서 약물 복용 전 간기능 수치와 약물 복용 후 간기능 수치를 비교한다면 두 개의 값은 "한 사람"에서 나왔기 때문에 독립이라고 볼 수 없다. 이런 경우 독립성을 만족한다고 볼 수 없다. 이런 경우 독립 표본 t 검정이 아닌 대응 표본 t 검정을 사용하는 것과 일맥상통한다. 유전적 정보를 공유하는 가족이나, 같은 경험을 하는 같은 반 학생들은 (항상 그런 것은 아니지만) 가끔 일반적인 선형 회귀 분석이 적절하지 않을 수 있다.
나머지 세 가지 전제조건에 대해 검증을 해보도록 하겠다.
*실습용 데이터는 아래 링크를 클릭하면 다운로드할 수 있습니다.
2022.08.04 - [공지사항 및 소개] - 분석용 데이터 (update 22.12.18)
분석용 데이터 (update 22.12.18)
2022년 12월 18일 버전입니다. 변수는 계속하여 추가될 예정입니다. 다음 카테고리에 있는 글에서 이용된 데이터입니다. - 기술 통계 - 범주형 자료 분석 - 모평균 검정 - 상관분석 - 반복 측정 자료
medistat.tistory.com
코드를 보여드리기에 앞서 워킹 디렉토리부터 지정하겠다.
워킹 디렉토리에 관한 설명은 다음 링크된 포스트에서 볼 수 있다.
2022.08.05 - [통계 프로그램 사용 방법/R] - [R] 작업 디렉토리 (Working Directory) 지정 - getwd(), setwd()
setwd("C:/Users/user/Documents/Tistory_blog")
데이터를 불러와 df에 객체로 저장하겠다.
데이터 불러오는 방법은 다음 링크에서 볼 수 있다.
2022.08.05 - [통계 프로그램 사용 방법/R] - [R] 데이터 불러오기 : EXCEL - read_excel(), read.xlsx()
2022.08.10 - [통계 프로그램 사용 방법/R] - [R] 데이터 저장하기 : CSV 파일 - write.csv(), write_csv()
2022.08.10 - [통계 프로그램 사용 방법/R] - [R] 데이터 불러오기 : SAS file (.sas7bdat) - read.sas7bdat(), read_sas()
install.packages("readr")
library("readr")
df<-read_csv("Data.csv")
목표: 수축기 혈압(SBP)과 심혈관 질환 위험 점수 (CVD_RISK) 사이의 선형 회귀 분석의 전제조건이 성립하는가?
먼저 선형 회귀 분석을 실시한다. (2022.12.22 - [선형 회귀 분석/R] - [R] 단순 선형 회귀 분석 (Simple linear regression) - lm())
LR_SBP_CVD<-lm(CVD_RISK~SBP, data=df)
R은 참 고맙게도, plot() 함수 안에 선형 회귀 분석을 실시한 객체를 넣어주면 전제 조건 확인을 위한 그래프를 바로 보여준다.
코드
plot(LR_SBP_CVD)실시 후 엔터(Window) 혹은 Return(Mac)을 누르면 4개의 그래프를 보여주며, 우리는 마지막 그림을 제외하고 앞 세 개의 그래프만 사용할 것이다.
결과
1) 잔차의 정규성 (Normality)
2번째 나오는 그림을 이용한다.
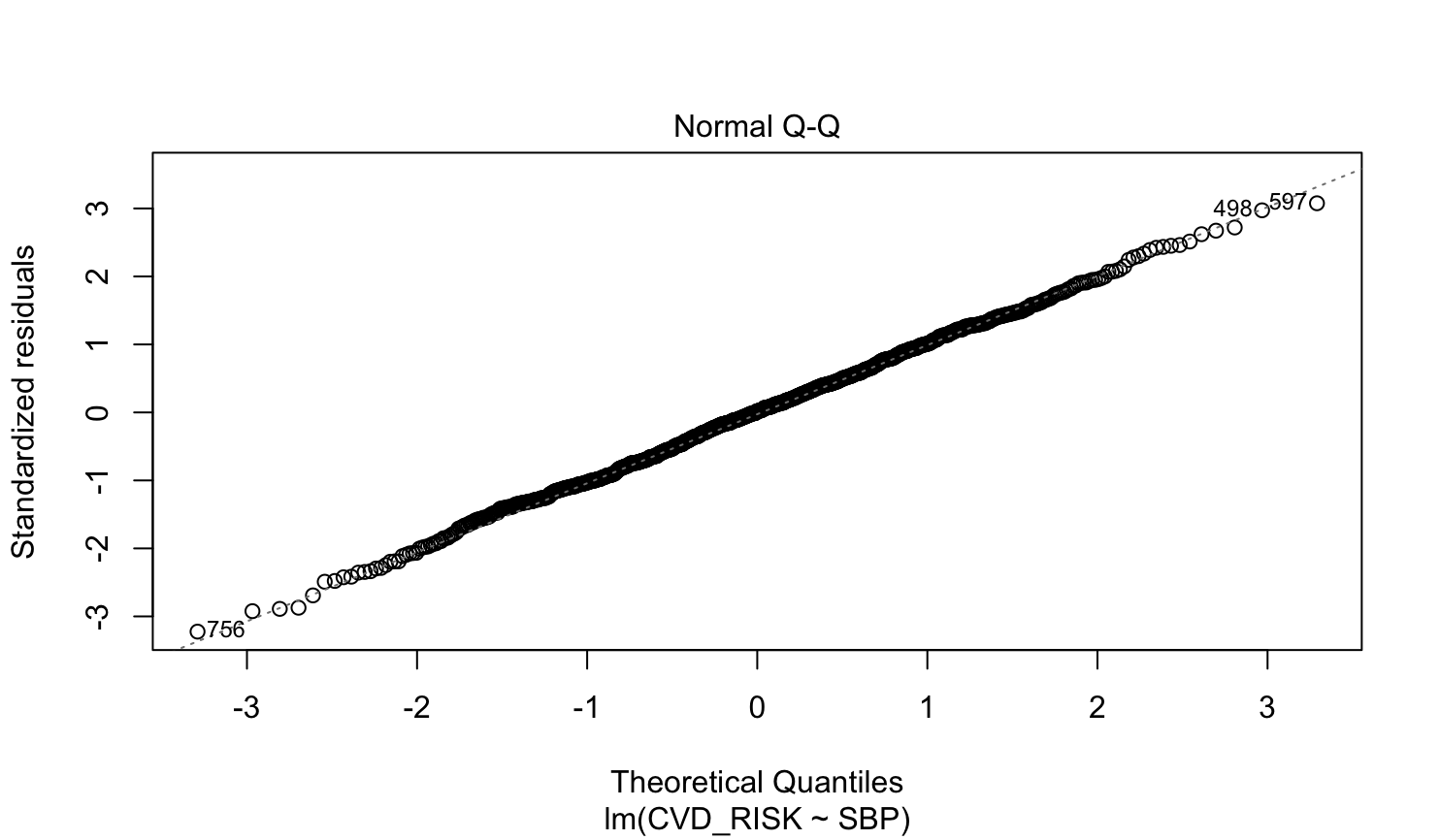
일반 Q-Q plot처럼 해석하면 된다. (Q-Q plot내용은 다음 포스팅을 참고하길 바란다.2022.08.11 - [기술 통계/R] - [R] 정규성 검정 (1) : Q-Q plot - qqnorm(), qqline()) 대부분의 점이 45도의 점선 상에 있는 것을 알 수 있다. (비록 $x$축과 $y$축의 scale이 달라 45도처럼 보이지 않으나, $y=x$직선이다.) 따라서 잔차는 정규성을 따른다고 할 수 있다.
2) 선형성 (Linearity)
첫 번째 나오는 그림을 이용한다.
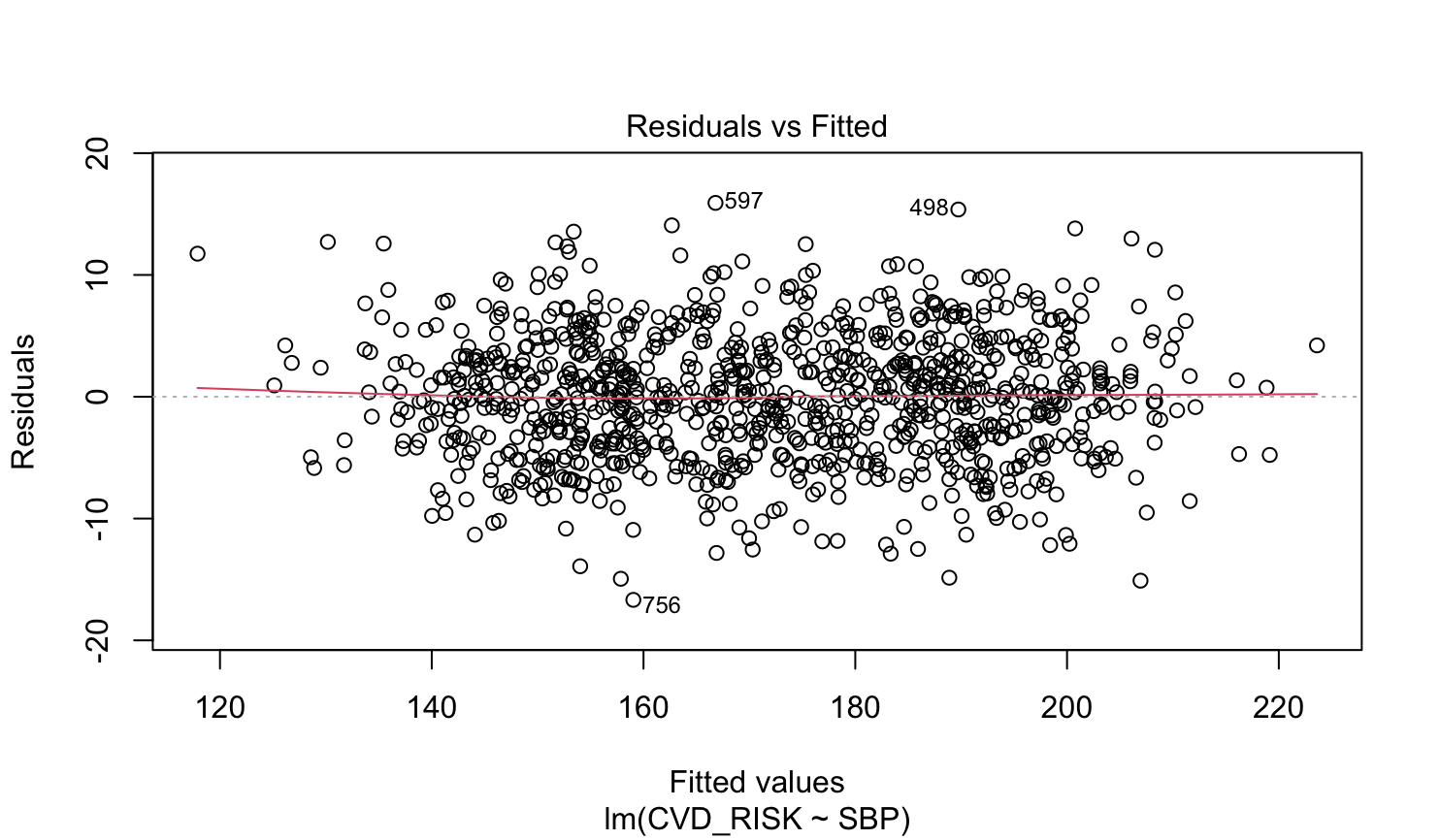
해석 방법: Residual이 0 위아래에 고루 분포하며 특정한 형태나 패털을 보이지 않는다. 즉, 점선 위나 아래에 몰려있는 공간이 있으면 안 된다. 예를 들어 Fitted Values가 140인 근방에서는 Residuals이 0보다 큰 게 많고, 200인 근방에서는 0보다 작은 게 많은 상황이 발생했다면 선형성이 망가진 것이다.
여기서 유의할 것은 절대로 일반적인 산포도로 선형성을 확인하면 안 된다는 것이다. 이유로는 다음 두 가지를 들 수 있다.
1) 독립변수가 여러 개인 다중 선형 회귀 분석에서는 차원의 문제로 산포도로 선형성을 확인하는 것이 쉽지 않다.
2) 단순한 변수의 산포도를 확인하면 안 된다. 예를 들어 A와 B의 선형 회귀 분석을 시행할 것인데 A는 로그 변환하여 사용하기로 했다면 산포도는 A와 B의 산포도가 아니라, log(A)와 B의 산포도를 확인해야 한다.
3) 등분산성 (Homoscedasticity)
세 번째 나오는 그림을 사용한다.

해석 방법: 점들이 어떤 직사각형 안에 고루 퍼져있다면 등분산성을 만족한다. 그러므로 본 사례는 등분산성을 만족한다.
설명의 용이성을 위해 단순 선형 회귀 분석에서 "잔차의 등분산성"의 의미는 다음과 같다. "각 SBP값에 대해 잔차의 분산은 같다." 그림으로 설명하면 다음 그림에서, 주황 박스 안의 잔차들의 분산이 파란 박스 안의 잔차들의 분산과 같다는 것이다. 물론 박스는 저 두 곳에만 위치하는 것이 안이라 전 구간에 걸쳐 존재하게 된다.
따라서, 점들이 어떤 직사각형 안에 고루 퍼져있지 않고, 특정 Fitted value에서만 넓게 퍼져있거나 좁게 분포해 있다면 등분산성 가정에 위배되게 될 것이다.
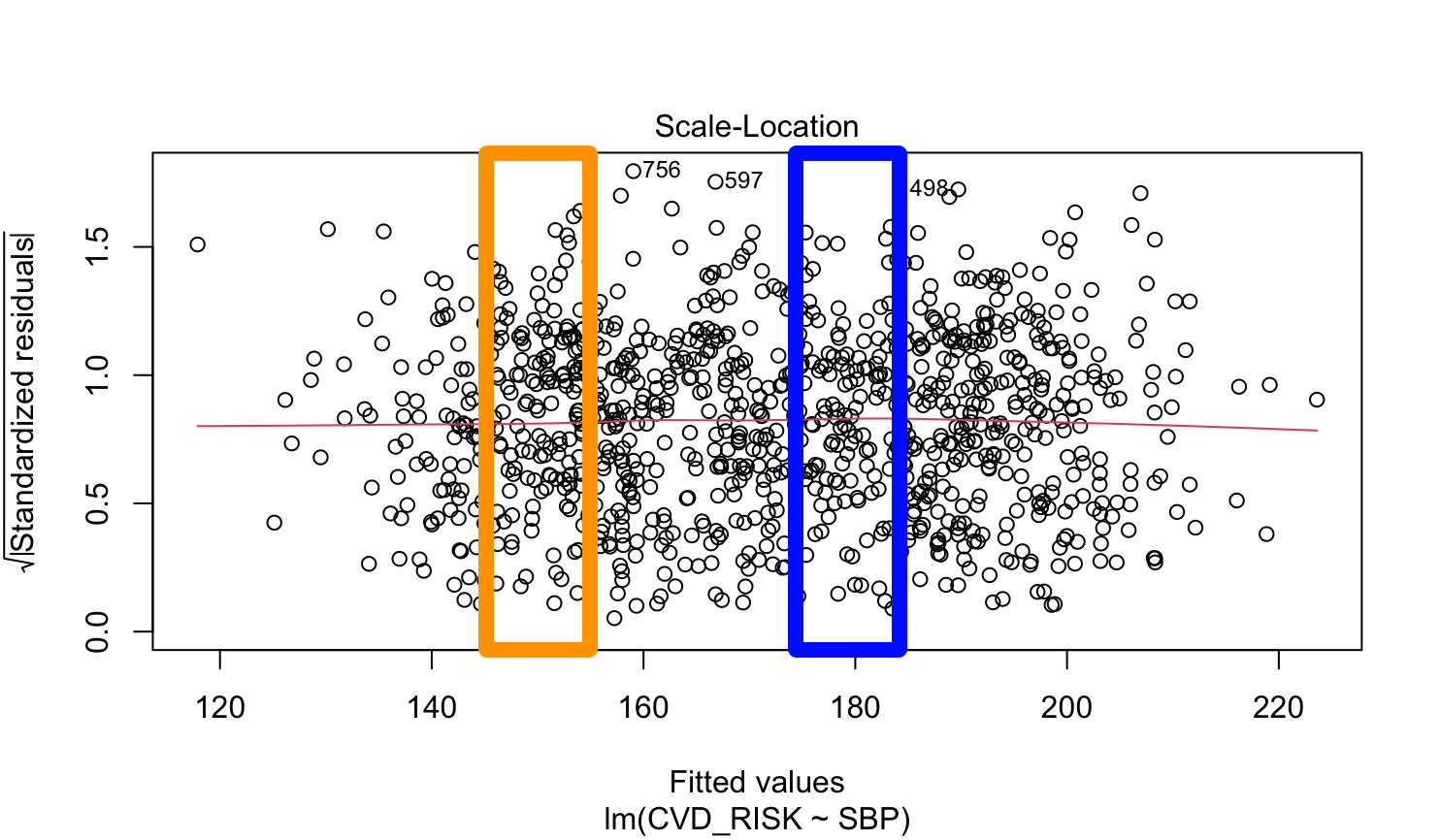
만약 단순 선형 회귀 분석이 아니라 다중 선형 회귀 분석인 경우 "각 SBP(독립 변수) 값에 대해 잔차의 분산은 같다."가 아니라 "예측된 종속 변수(CVD_RISK) 값에 대해 잔차의 분산은 같다."가 될 것이다.
주관적이지 않나?
위 분석들은 모두 주관적으로 결론 내리고 있는 것이 사실이다. 통계적으로 어떤 p-value를 내는 검정 방법이 충분히 존재하겠지만, 현재로서는 대부분은 주관적으로만 판단을 내리고 있는 것이 현실이다. 세상이 바뀌고 객관적인 결정을 내리기를 요구하는 시대가 도래할지도 모르지만, 만약 그런 세대가 온다면, 아마도 위 전제 조건들을 엄격하게 모두 만족하는 데이터는 그리 많지 않을 것이다. 아마 현재로서도 이러한 현실적인 이유 때문에 그렇게까지 가정을 검정하라고 하지는 않는 것 같다.
하지만 제안된 통계적 방법은 존재한다. 바로 Edsel의 Global Validation of Linear Models Assumptions(GVLMA)다. 이는 gvlma패키지의 gvlma() 함수로 시행할 수 있다.
코드
#gvlma 패키지 설치
install.packages("gvlma")
library("gvlma")
#gvlma 시행
gv<-gvlma(LR_SBP_CVD)
summary(gv)gv<-gvlma(LR_SBP_CVD) : 위에서 시행한 선형 회귀 분석 결과를 gvlma함수에 넣고 그 내용을 gv객체에 저장한다.
summary(gv) : gv 내용을 보여달라
결과
Value p-value Decision
Global Stat 1.8578 0.7619 Assumptions acceptable.
Skewness 0.0394 0.8427 Assumptions acceptable.
Kurtosis 0.1602 0.6890 Assumptions acceptable.
Link Function 1.1687 0.2797 Assumptions acceptable.
Heteroscedasticity 0.4895 0.4841 Assumptions acceptable.Value p-value Decision
Global Stat 1.8578 0.7619 Assumptions acceptable.
: 아래 네 개를 종합적으로 판단한 결과다. p-value>0.05이므로 종합적으로 선형 회귀 분석의 가정이 성립한다고 본다.
Skewness 0.0394 0.8427 Assumptions acceptable.
: 정규성 판정 중 Skewness기준으로 본 것이다. 정규분포의 Skewness는 0이므로 0에 가까울수록 정규성을 따른다고 보며, p-value>0.05이므로 이 항목은 선형 회귀 분석의 가정이 성립한다고 본다.
Kurtosis 0.1602 0.6890 Assumptions acceptable.
: 정규성 판정 중 Kurtosis기준으로 본 것이다. 정규분포의 Kurtosis는 0이므로 0에 가까울수록 정규성을 따른다고 보며, p-value>0.05이므로 이 항목은 선형 회귀 분석의 가정이 성립한다고 본다.
Link Function 1.1687 0.2797 Assumptions acceptable.
: link function을 제대로 설정했는가에 대한 항목으로 p-value>0.05이므로 이 항목은 선형 회귀 분석의 가정이 성립한다고 본다.
Heteroscedasticity 0.4895 0.4841 Assumptions acceptable.
: 등분산성에 대한 항목이고 p-value>0.05이므로 이 항목은 선형 회귀 분석의 가정이 성립한다고 본다.
그런데, 왜 하필이면 이런 가정이 필요한걸까? 이는 선형회귀분석으로 구한 회귀계수들이 참값이기 위한 가정이며, 이 가정들을 가우스-마르코프 정리 (Gauss-Markov theorem)라고 한다. 관련 내용은 다음 링크에서 확인할 수 있다. 2023.06.21 - [통계 이론] - [이론] 가우스-마르코프 정리 (Gauss-Markov Theorem)
코드 정리
##워킹 디렉토리 지정
setwd("C:/Users/user/Documents/Tistory_blog")
##데이터 불러오기
install.packages("readr")
library("readr")
df<-read_csv("Data.csv")
#회귀 분석 시행
LR_SBP_CVD<-lm(CVD_RISK~SBP, data=df)
#가정 확인 방법 1
plot(LR_SBP_CVD)
#가정 확인 방법 2
#gvlma 패키지 설치
install.packages("gvlma")
library("gvlma")
#gvlma 시행
gv<-gvlma(LR_SBP_CVD)
summary(gv)[R] 선형 회귀 분석의 전제 조건 정복 완료!
작성일: 2022.12.22.
최종 수정일: 2023.10.17.
이용 프로그램: R 4.2.2
RStudio v2022.07.2
RStudio 2022.07.2+576 "Spotted Wakerobin" Release
운영체제: Windows 10, Mac OS 12.6.1
'선형 회귀 분석 > R' 카테고리의 다른 글
| [R] 선형 회귀 분석의 모델 최적화 : 전진 선택법, 후진 제거법 - lm(), step() (1) | 2022.12.23 |
|---|---|
| [R] 다중 선형 회귀 분석 (Multiple linear regression) - lm(), factor() (0) | 2022.12.23 |
| [R] 범주형 변수의 선형 회귀 분석 (Simple linear regression with categorical variable) - lm(), factor() (1) | 2022.12.22 |
| [R] 단순 선형 회귀 분석 (Simple linear regression) - lm() (0) | 2022.12.22 |