
[SAS] 대응 표본 T검정 (Paired samples T-test) - PROC TTEST
세상에 존재하는 모든 사람을 대상으로 연구를 하면 참 좋겠지만, 시간적인 이유로, 그리고 경제적인 이유로 일부를 뽑아서 연구를 진행할 수밖에 없다. 모든 사람을 모집단이라고 하고, 뽑힌 일부를 표본이라고 한다. 우리는 표본으로 시행한 연구로 모집단에 대한 결론을 도출해내고자 할 것이다.
1000명에게 피검사를 시행하였고, 간 기능 검사의 일환으로 ALT 수치를 모았다. 그리고, 간 기능 개선제를 복용시킨 뒤 ALT 검사를 다시 시행하였다. 이 데이터를 기반으로 1000명이 기원한 모집단 인구에서 간 기능 개선제 복용은 ALT 수치를 개선시키는지 여부를 확인하는 것이 T-test이다. T-test는 크게 세 가지로 나눌 수 있다.
1) 일표본 T검정 (One sample T-test) : 2022.09.30 - [모평균 검정/SAS] - [SAS] 일표본 T검정 (One-sample T-test) - PROC TTEST
: 모집단의 평균이 특정 값이라고 할 수 있는가?
예) 모집단의 ALT 평균이 50이라고 할 수 있는가?
2) 독립 표본 T검정 (Independent samples T-test, Two samples T-test) : 2022.10.04 - [모평균 검정/SAS] - [SAS] 독립 표본 T검정 (Independent samples T-test) - PROC TTEST
: 두 모집단의 평균이 다르다고 할 수 있는가?
예) 고혈압 환자와 일반인의 수축기 혈압 평균이 서로 다르다고 할 수 있는가?
3) 대응 표본 T검정 (Paired samples T-test)
: 모집단의 짝지어진 변수들의 평균이 다르다고 할 수 있는가?
예) 간 기능 개선제 복용 전 ALT 평균은 간기는 개선제 복용 후 ALT 평균과 다르다고 할 수 있는가?
이번 포스팅에서는 대응 표본 T검정 (Paired samples T-test)에 대해 알아볼 것이다.
왜 대응 표본 T 검정이 필요할까?
독립 표본 T 검정을 공부한 사람이라면 대응 표본 T 검정의 필요성에 대해 의구심을 가질 수 있다. 간 기능 개선제 복용 전 ALT와 간 기능 개선제 복용 후 ALT에 대해 독립 표본 T 검정을 돌리면 될 것이라고 생각할 수 있기 때문이다. 하지만 결론적으로 그렇게 하면 안 된다. 예를 들어 다음 사례를 봐보자.
| 환자 번호 | 시험 공부 전 시험 점수 | 시험 공부 후 시험 점수 |
| 1번 | 0.1 | 0.2 |
| 2번 | 0.2 | 0.3 |
| ... | $x$ | $x+0.1$ |
| 999번 | 99.9 | 100.0 |
| 1000번 | 100.0 | 100.0 |
1000명이 시험을 보았고, 원래 100점을 받았던 1000번을 제외한 모든 사람이 시험공부로 0.1점이 올랐다. 1000명 중 999명의 점수가 올랐으므로 공부는 시험 점수를 올리는데 유의미한 영향력을 미칠 수 있다고 결론이 나야 합당할 것이다. 하지만 공부 전 후 시험 점수의 평균은 둘 다 50점에 가깝고 큰 변화는 없는 것처럼 보인다. 따라서 독립 표본 T 검정으로 내린 결론은 잘못된 것이다. 즉, 대응되는 (paired) 경우 그 값 자체보다는 둘 사이의 차이에 집중해야 한다.
*실습용 데이터는 아래 링크를 클릭하면 다운로드할 수 있습니다.
2022.08.04 - [공지사항 및 소개] - 분석용 데이터 (update 22.10.06)
분석용 데이터 (update 22.10.06)
2022년 08월 29일 버전입니다. 변수는 계속하여 추가될 예정입니다. 다음 카테고리에 있는 글에서 이용된 데이터입니다. - 기술 통계 - 통계 프로그램 사용 방법 1) 엑셀 파일 2) CSV 파일 3) 코드북
medistat.tistory.com
시작하기 위해 라이브러리를 만들고, 파일을 불러온다.
라이브러리 만드는 방법: 2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 라이브러리 만들기 - LIBNAME
파일 불러오는 방법: 2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 데이터 불러오기 및 저장하기 - PROC IMPORT, PROC EXPORT
*라이브러리 지정하기;
LIBNAME hong "C:/Users/User/Documents/Tistory_blog";
*파일 불러오기;
PROC IMPORT
DATAFILE="C:\Users\user\Documents\Tistory_blog\Data.xlsx"
DBMS=EXCEL
OUT=hong.df
REPLACE;
RUN;
전제: 정규성 검정 (차이)
대응 표본 T 검정 (Paired samples T test)의 전제 조건은 검정하고자 하는 두 변수의 차이가 정규분포를 따른다는 것이다. 따라서 ALT와 간 기능 개선제 복용 후 ALT(ALT_POSTMED)의 차이를 구하고 정규성 검정을 시행한다.
차이를 구하는 방법: 2022.10.06 - [통계 프로그램 사용 방법/SAS] - [SAS] 변수 계산 (산술 연산) - DATA, SET
정규성 검정을 하는 방법: 2022.08.12 - [기술 통계/SAS] - [SAS] 정규성 검정 - PROC UNIVARIATE
DATA hong.df;
SET hong.df;
*차이를 나타내는 변수는 ALT_DIF;
ALT_DIF=ALT-ALT_POSTMED;
RUN;
PROC UNIVARIATE DATA=hong.df NORMAL PLOT;
VAR ALT_DIF;
HISTOGRAM ALT_DIF/ NORMAL (MU=EST SIGMA=EST);
RUN;
결과
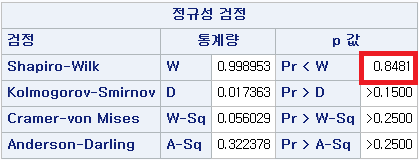
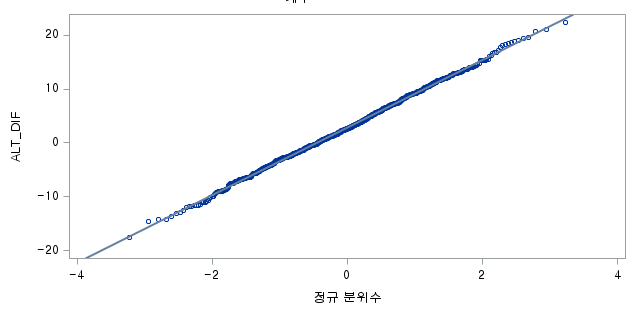
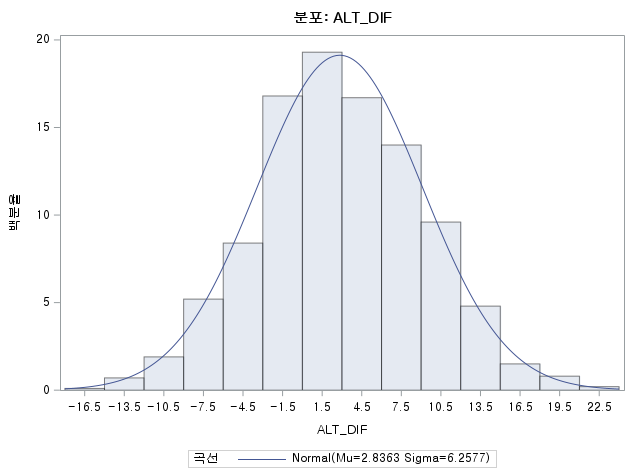
N 수는 1000으로 2000 미만이므로 Shapiro-Wilk 통계량의 p-value는 0.05 이상이다. Q-Q plot상에서 대부분의 데이터가 직선상에 있으며, 히스토그램 또한 정규분포를 따르는 것처럼 보이므로 두 변수의 차는 정규분포를 따른다고 할 수 있다. 따라서 대응 표본 T 검정 (Paired samples T test)를 시행할 수 있다.
대응 표본 T 검정 코드
PROC TTEST DATA=hong.df;
PAIRED ALT*ALT_POSTMED;
RUN;
PROC TTEST DATA=hong.df; : T-test를 시행할 것이고, 데이터는 hong 라이브러리의 df 데이터를 이용하라.
PAIRED ALT*ALT_POSTMED; : 대응 표본 T 검정(PAIRED)을 시행할 것이고, 각각의 변수는 ALT와 ALT_POSTMED이다.
결과
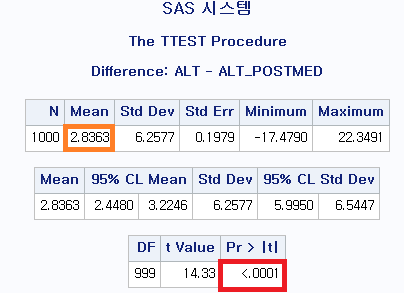
ALT의 평균이 ALT_POSTMED의 평균에 비해 2.8363만큼 더 크다. 그리고 그 차이의 p-value는 <0.0001로 유의미하다. 따라서 귀무가설을 기각할 수 있다. 본 검정의 귀무가설은 다음과 같다.
귀무가설: $H_0$=간 기능
이를 기각하므로 동일하지 않다고 할 수 있고, 간 기능 개선제 복용 후 ALT가 2.8363만큼 낮아져 간 기능에 호전이 있다고 평가할 수 있다.
$$ALT = ALT\_POSTMED$$
$$ \therefore ALT\_DIF=ALT-ALT\_POSTMED=0$$
즉, 대응 표본 T 검정을 시행하는 것은 ALT_DIF변수의 평균이 0과 같은지 검정하는 일표본 T검정 (One sample T test)와 같은 것이다. 일표본 T 검정은 다음 링크에서 확인할 수 있다. 2022.09.30 - [모평균 검정/SAS] - [SAS] 일표본 T검정 (One-sample T-test) - PROC TTEST
일표본 T 검정으로 대응 표본 T 검정 시행하기 - 코드
PROC TTEST DATA=hong.df H0=0;
VAR ALT_DIF;
RUN;
결과
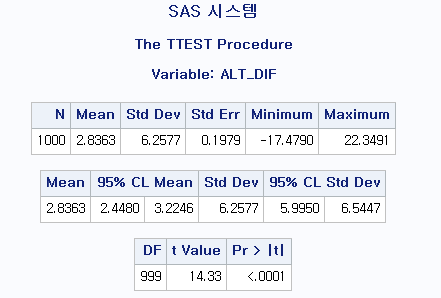
위와 같은 결과를 내는 것을 알 수 있다.
코드 정리
*라이브러리 지정하기;
LIBNAME hong "C:/Users/User/Documents/Tistory_blog";
*파일 불러오기;
PROC IMPORT
DATAFILE="C:\Users\user\Documents\Tistory_blog\Data.xlsx"
DBMS=EXCEL
OUT=hong.df
REPLACE;
RUN;
*차이를 나타내는 변수 만들기;
DATA hong.df;
SET hong.df;
*차이를 나타내는 변수는 ALT_DIF;
ALT_DIF=ALT-ALT_POSTMED;
RUN;
*정규성 검정 시행하기;
PROC UNIVARIATE DATA=hong.df NORMAL PLOT;
VAR ALT_DIF;
HISTOGRAM ALT_DIF/ NORMAL (MU=EST SIGMA=EST);
RUN;
*대응 표본 T 검정 시행하기 (1);
PROC TTEST DATA=hong.df;
PAIRED ALT*ALT_POSTMED;
RUN;
*대응 표본 T 검정 시행하기 (2);
PROC TTEST DATA=hong.df H0=0;
VAR ALT_DIF;
RUN;
SAS 대응 표본 T검정 (Paired samples T-test) 정복 완료!
작성일: 2022.10.07.
최종 수정일: 2022.10.07.
이용 프로그램: SAS v9.4
운영체제: Windows 10