[SAS] 크루스칼 왈리스 검정 (비모수 일원 배치 분산 분석: Kruskal-Wallis Test) - NPAR1WAY()
셋 이상의 분포에서 평균이 다른지 확인하는 방법은 ANOVA (ANalysis Of VAriance)였다.
2022.11.26 - [모평균 검정/SAS] - [SAS] 등분산 가정이 성립하지 않는 일원 배치 분산 분석 (Welch's ANOVA) - PROC GLM, PROC MIXED
그런데, 여기에는 각각의 분포가 정규성을 따른다는 중요한 가정이 필요하다. 하지만 정규성을 따르지 않는다면 어떻게 해야 할까? 그럴 때 사용하는 것이 크루스칼-왈리스 검정(Kruskal-Wallis Test)이다. 이번 포스팅에서는 크루스칼 왈리스 검정과 그 사후 분석 (post hoc analysis)까지 알아보고자 한다.
*실습용 데이터는 아래 링크를 클릭하면 다운로드할 수 있습니다.
2022.08.04 - [공지사항 및 소개] - 분석용 데이터 (update 22.12.18)
분석용 데이터 (update 22.12.18)
2022년 12월 18일 버전입니다. 변수는 계속하여 추가될 예정입니다. 다음 카테고리에 있는 글에서 이용된 데이터입니다. - 기술 통계 - 범주형 자료 분석 - 모평균 검정 - 상관분석 - 반복 측정 자료
medistat.tistory.com
시작하기 위해 라이브러리를 만들고, 파일을 불러온다.
라이브러리 만드는 방법: 2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 라이브러리 만들기 - LIBNAME
파일 불러오는 방법: 2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 데이터 불러오기 및 저장하기 - PROC IMPORT, PROC EXPORT
*라이브러리 지정하기;
LIBNAME hong "C:/Users/User/Documents/Tistory_blog";
*파일 불러오기;
PROC IMPORT
DATAFILE="C:\Users\user\Documents\Tistory_blog\Data.xlsx"
DBMS=EXCEL
OUT=hong.df
REPLACE;
RUN;
목표: 흡연 상태(SMOK)에 따라 니코틴 중독 점수 (NICOT_ADDICT) 중앙값이 모집단 수준에서 서로 다르다고 말할 수 있는가?
만약 NICOT_ADDICT의 분포가 정규성을 따른다면, ANOVA로 이를 확인할 수 있을 것이다. 따라서 정규성 여부를 먼저 확인해 보자.
정규성 - 코드
- 정규성 검정에 관한 분석 내용은 다음 글에서 살펴볼 수 있다. 2022.08.12 - [기술 통계/SAS] - [SAS] 정규성 검정 - PROC UNIVARIATE
- PROC UNIVARIATE명령문에서 "CLASS"옵션을 사용하는 방법은 다음 글에서 살펴볼 수 있다. 2022.09.23 - [기술 통계/SAS] - [SAS] 기술 통계 (평균, 표준편차, 표준오차, 최댓값, 최솟값, 중위수, 분위수 등) - PROC UNIVARIATE, PROC MEANS
PROC UNIVARIATE DATA=hong.df NORMAL PLOT;
CLASS SMOK;
VAR NICOT_ADDICT;
HISTOGRAM NICOT_ADDICT/ NORMAL (MU=EST SIGMA=EST);
RUN;정규성 - 결과
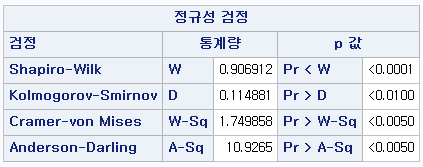
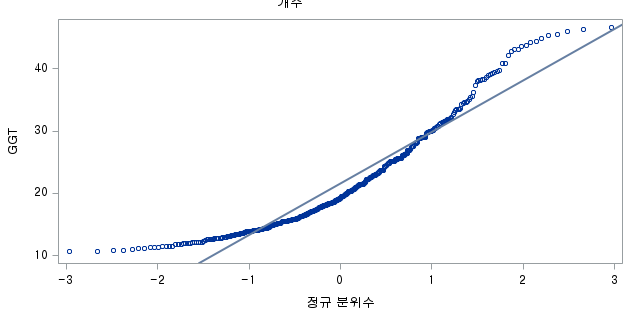
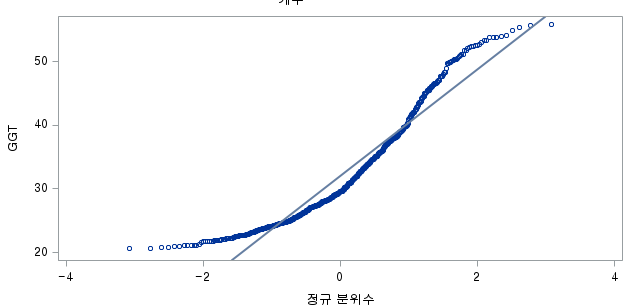
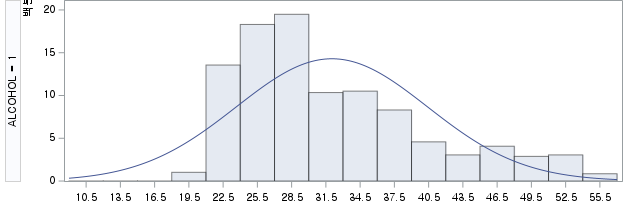
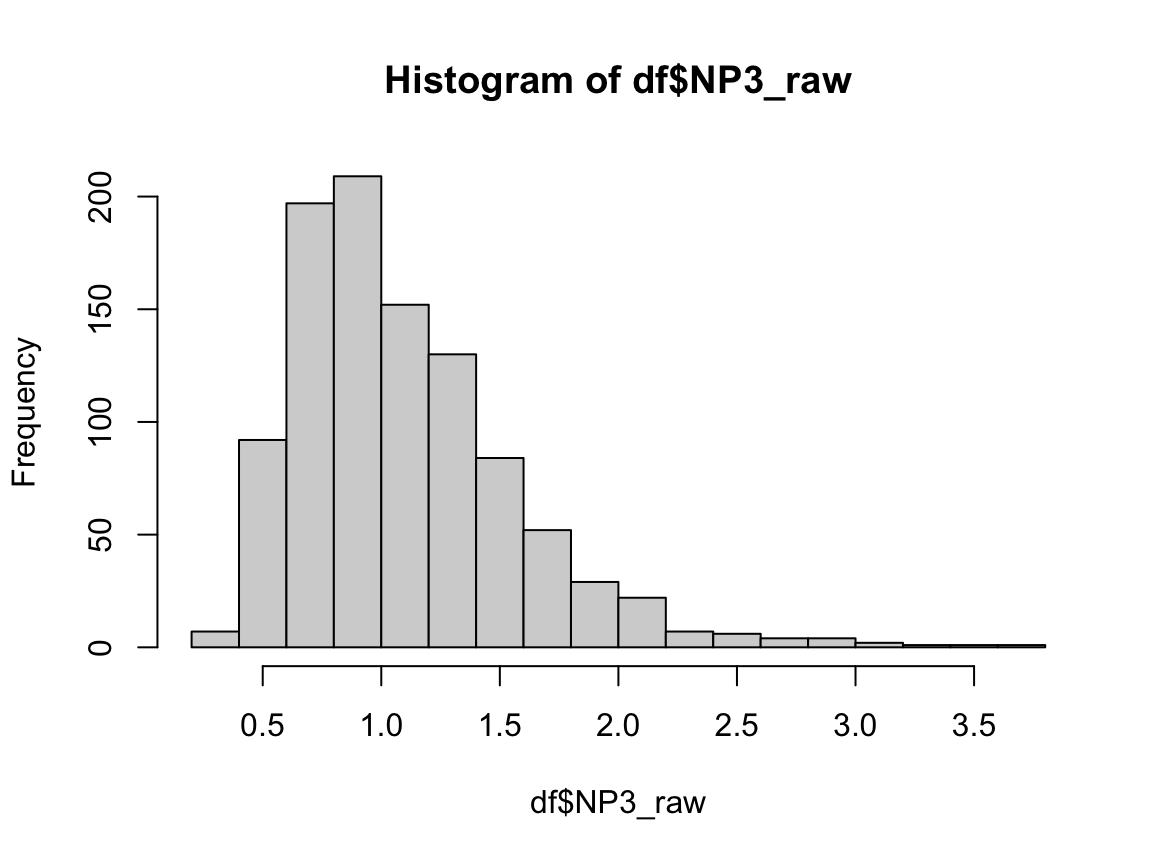
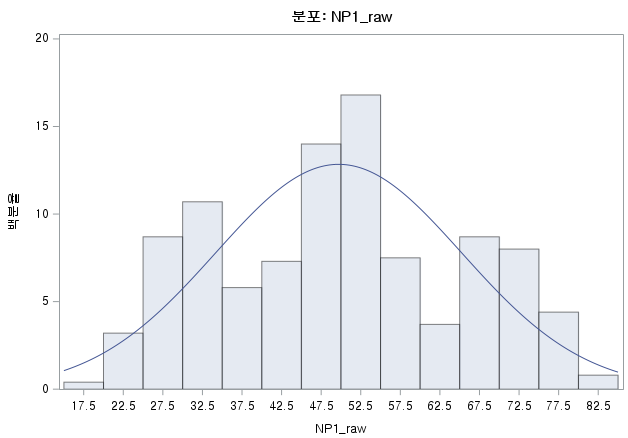
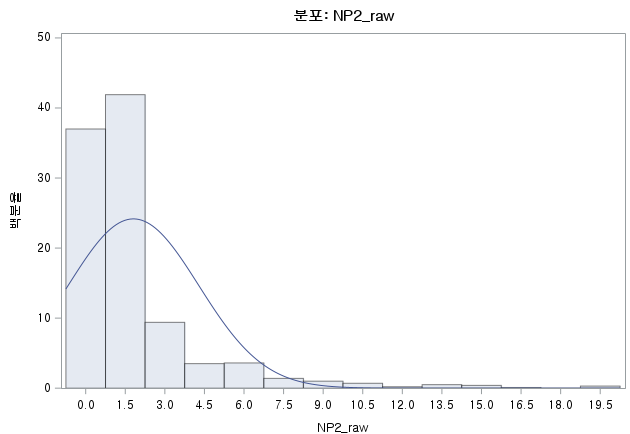
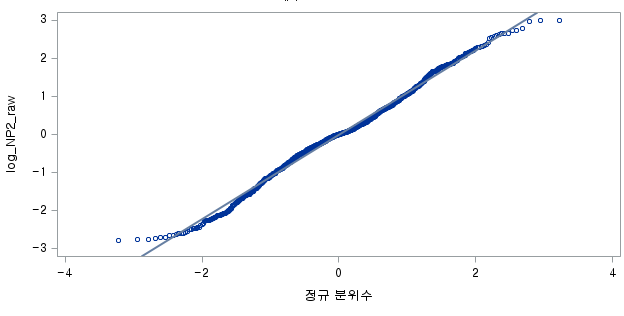
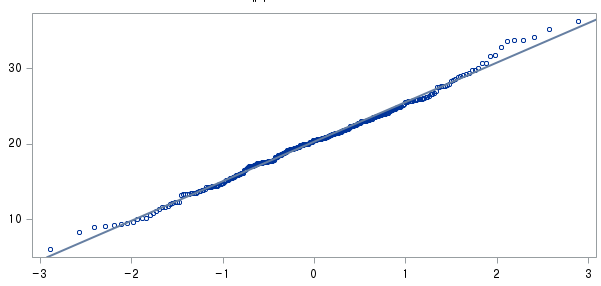
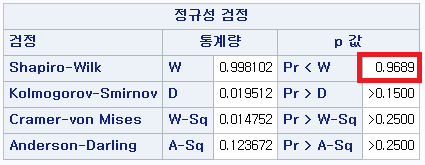
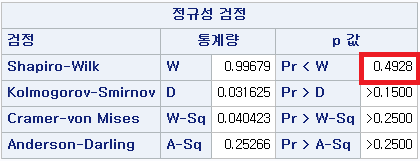
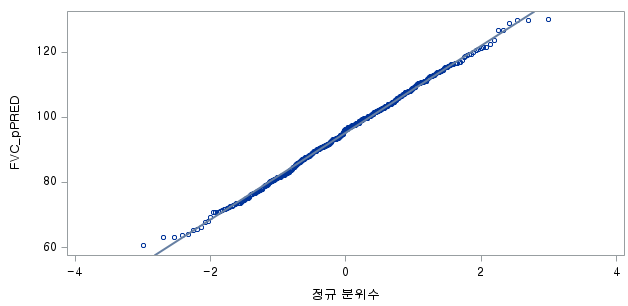
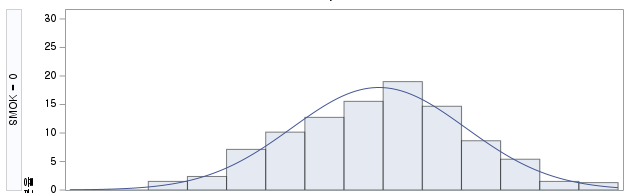
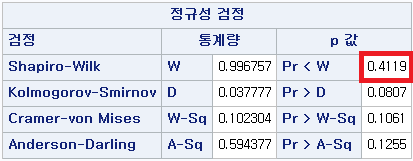
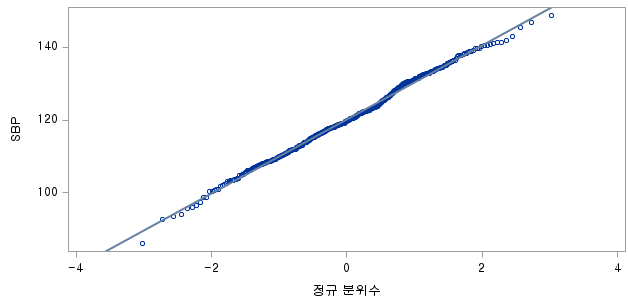
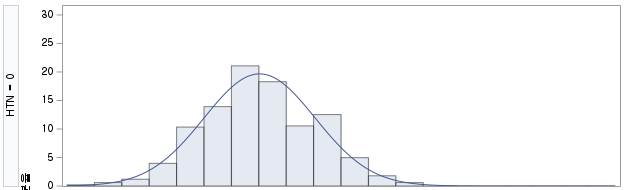
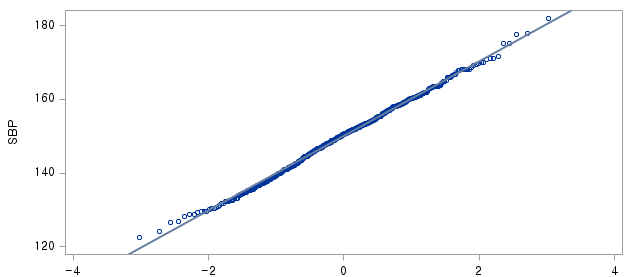
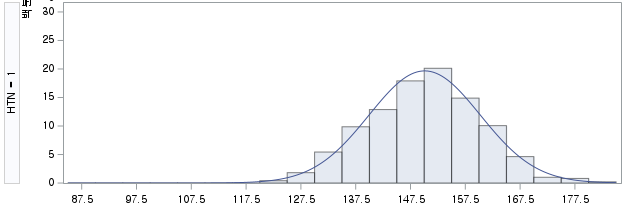
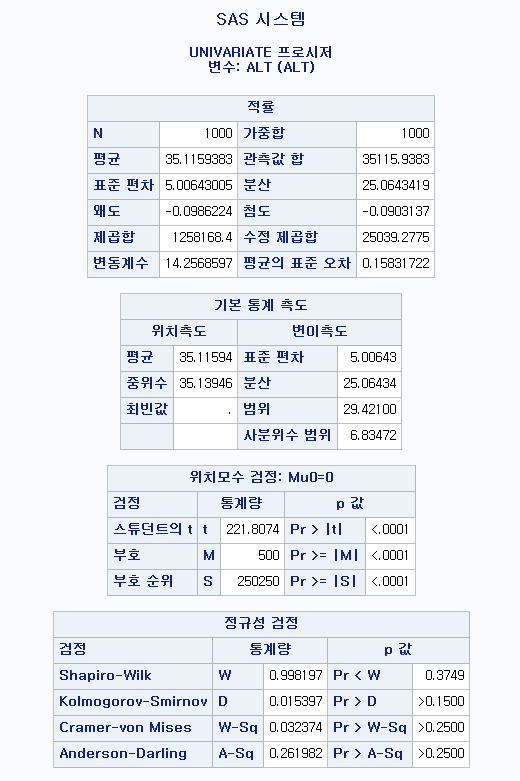
결과 - 1) 비흡연자 (SMOK=0)
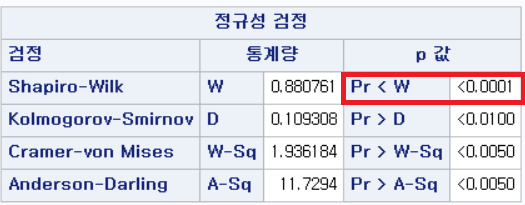
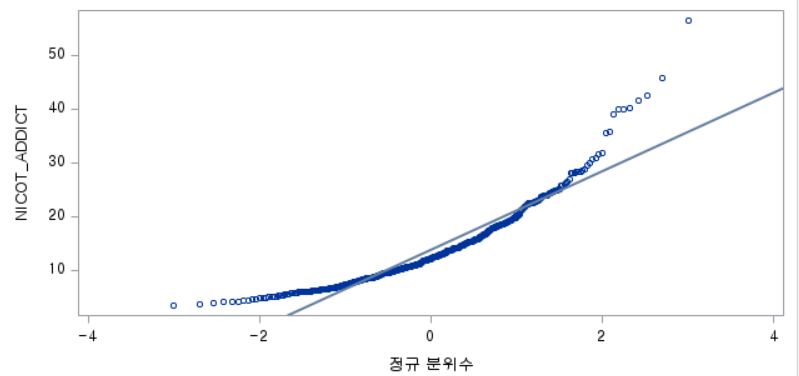
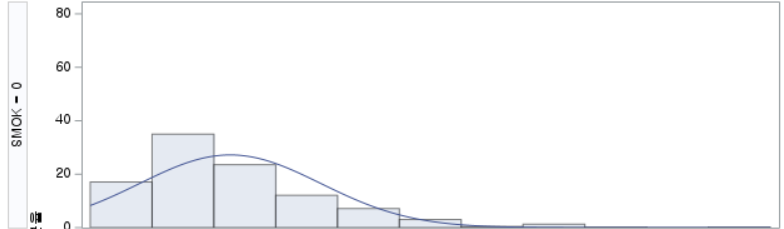
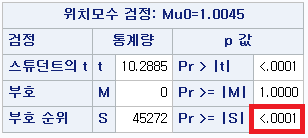
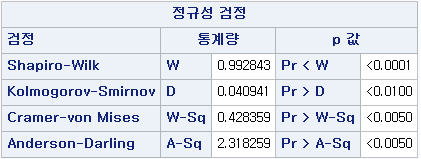
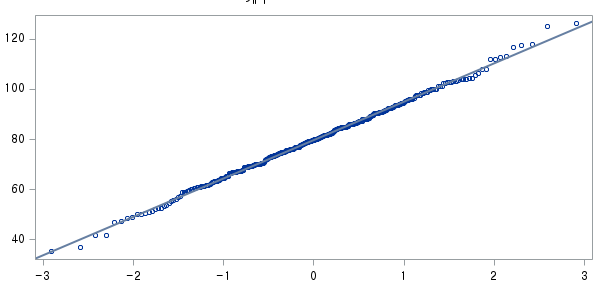
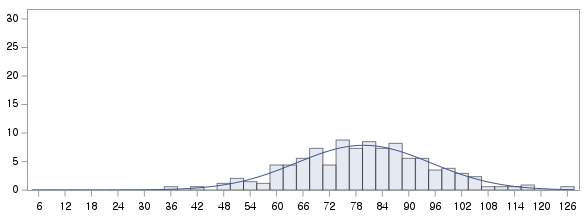
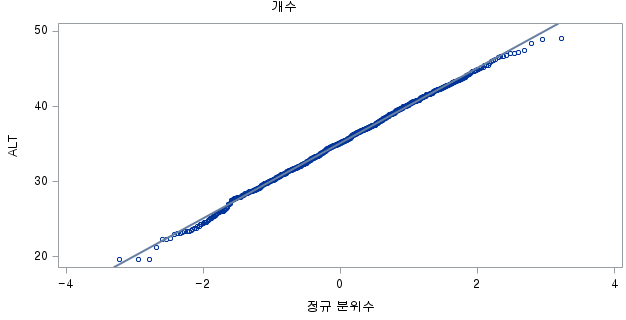
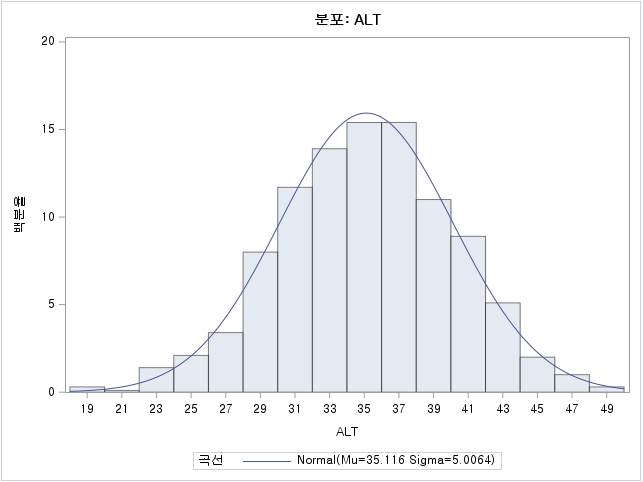
표본의 수가 2,000이 되지 않으므로 Shapiro-Wilk 통계량의 p-value를 보아야 하고, 이는 0.05보다 작다. Q-Q plot에서는 직선에서 벗어나는 표본들이 많고, 히스토그램에서도 right-skewed 분포를 보이므로 정규성을 따르지 않다고 결론을 짓는다.
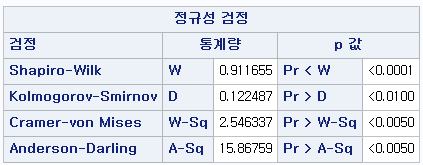
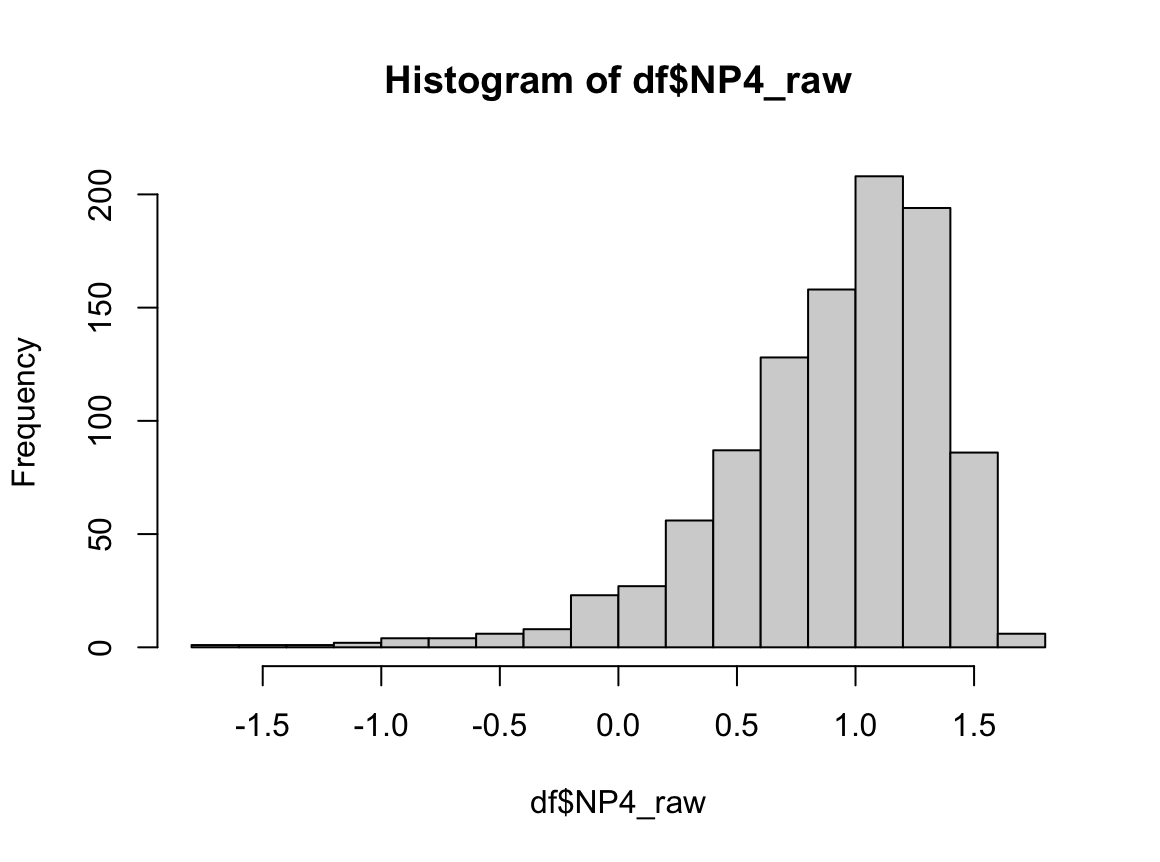
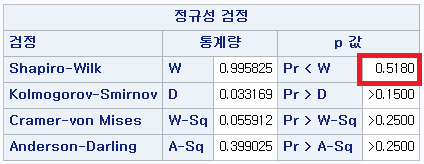
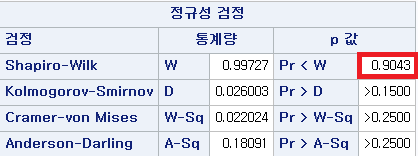
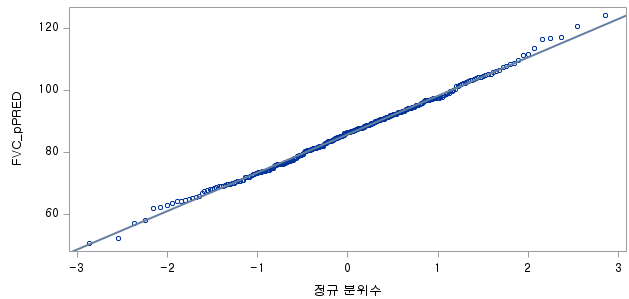
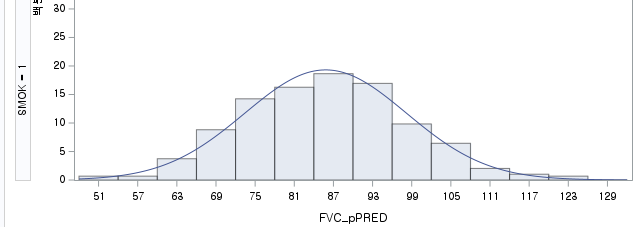
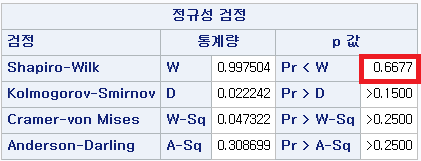
결과 - 2) 과거 흡연자 (SMOK=1)
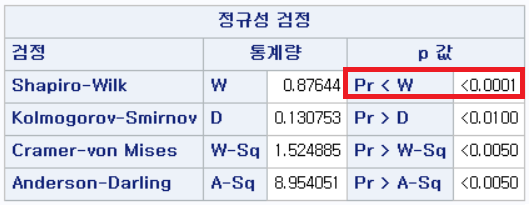
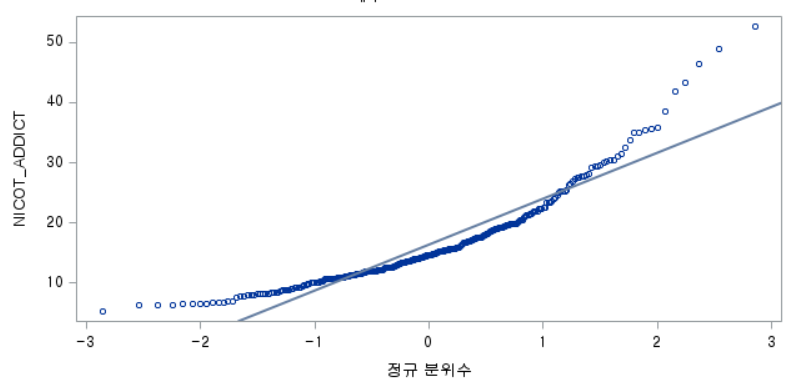
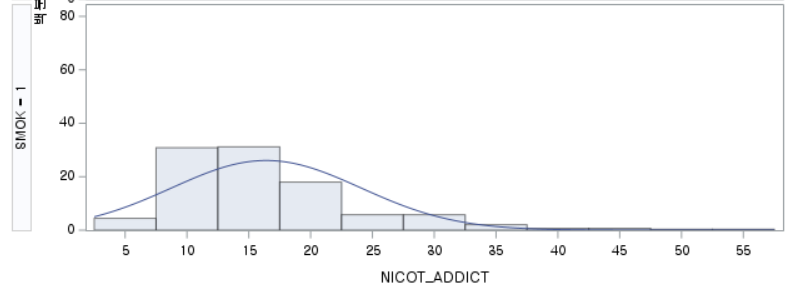
표본의 수가 2,000이 되지 않으므로 Shapiro-Wilk 통계량의 p-value를 보아야 하고, 이는 0.05보다 작다. Q-Q plot에서는 직선에서 벗어나는 표본들이 많고, 히스토그램에서도 right-skewed 분포를 보이므로 정규성을 따르지 않다고 결론을 짓는다.
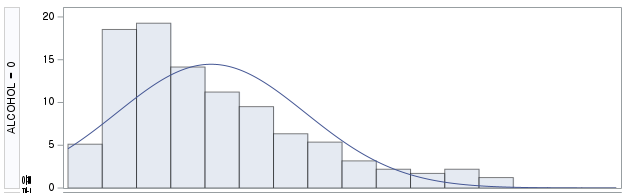
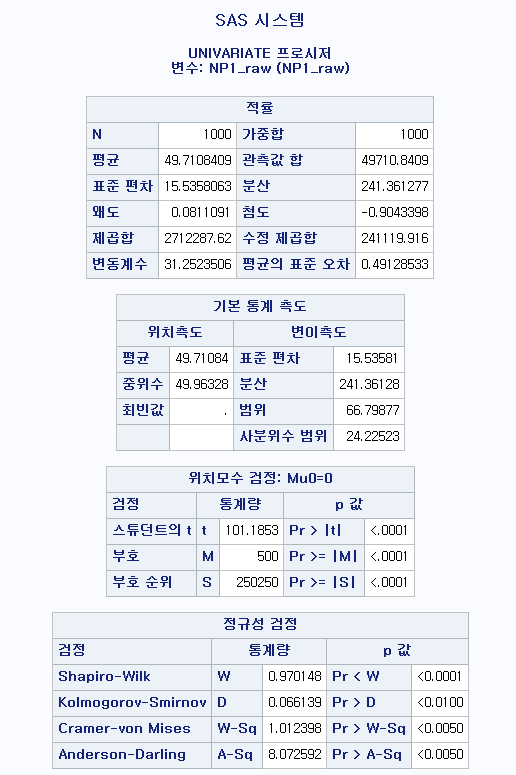
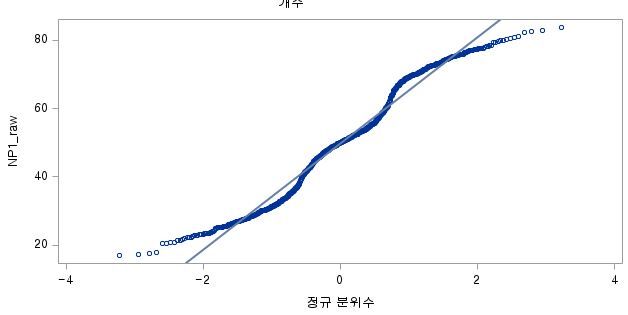
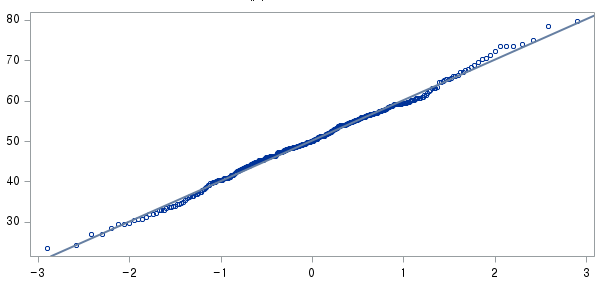
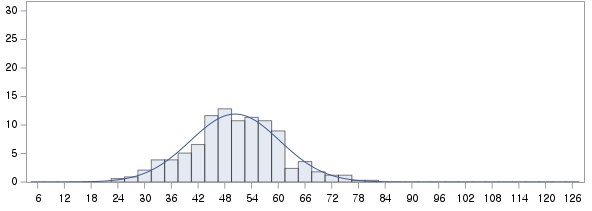
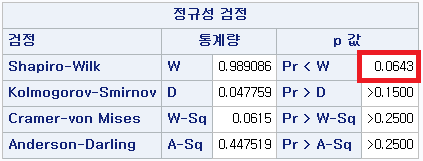
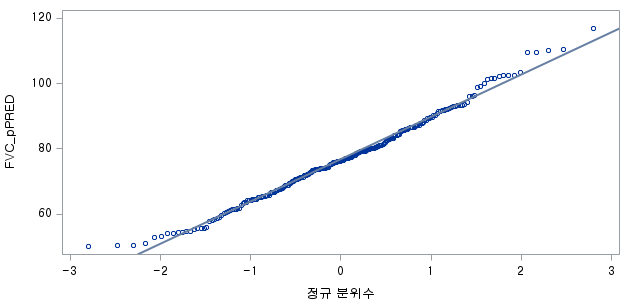
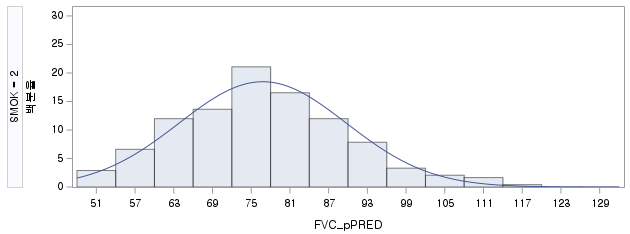
결과 - 3) 현재 흡연자 (SMOK=2)
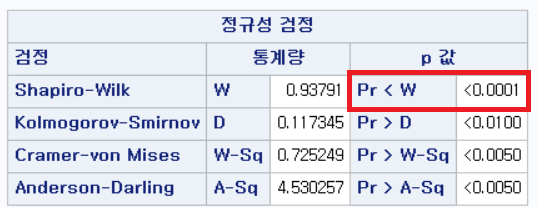
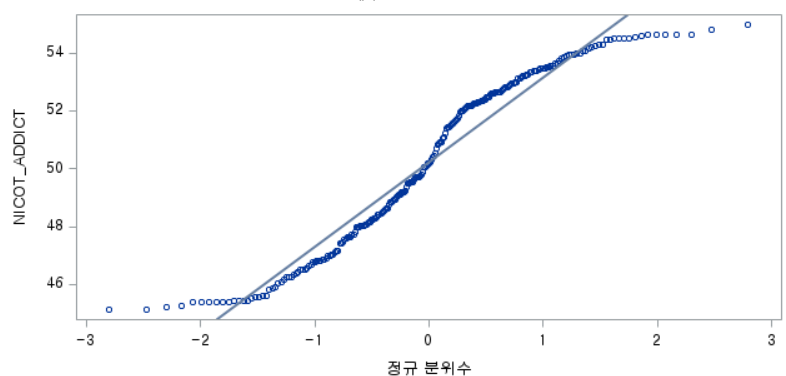
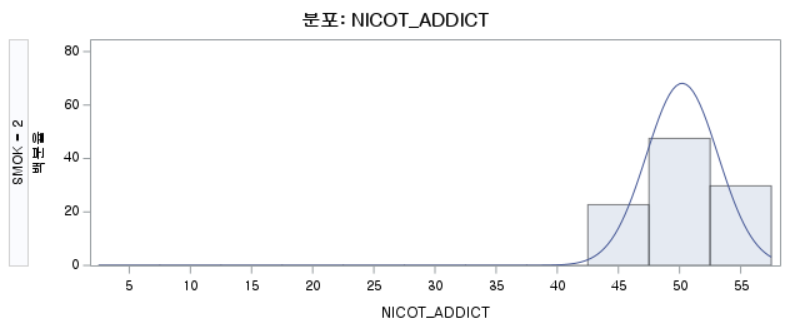
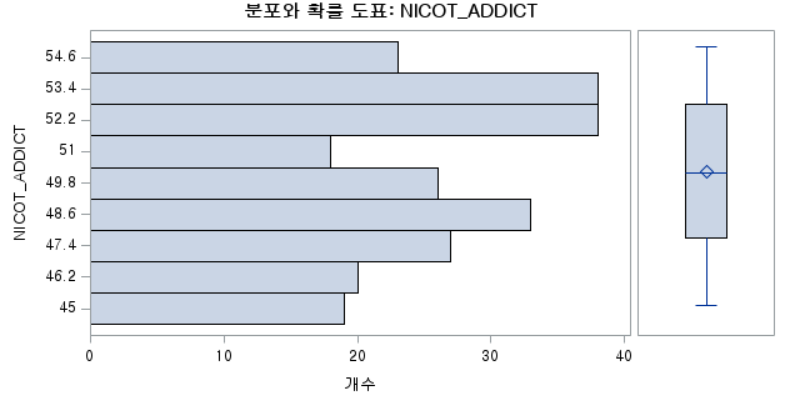
표본의 수가 2,000이 되지 않으므로 Shapiro-Wilk 통계량의 p-value를 보아야 하고, 이는 0.05보다 작다. Q-Q plot에서는 직선에서 벗어나는 표본들이 많고, 히스토그램에서도 uniform distribution 분포를 보이므로 정규성을 따르지 않다고 결론을 짓는다.
따라서 일원 배치 분산 분석 (ANOVA)을 시행할 수 없고, 크루스칼 왈리스 분석 (Kruskal-Wallis Test)을 시행해야 한다.
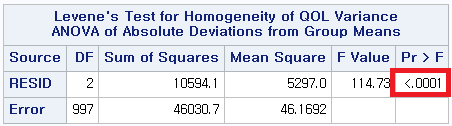
지금까지 많은 분석을 할 때 분산이 같은지 여부 (등분산성)을 중요하게 여겼었다. 하지만 크루스칼 왈리스 분석은 분산이 달라도 어느 정도 괜찮다. 물론 분산에 아주 큰 차이가 나면 위험해지지만, 어느 정도는 robust 하므로 웬만하면 그냥 써도 괜찮다.
크루스칼 왈리스 (Kruskal Wallis) 검정 코드
PROC NPAR1WAY DATA=hong.df WILCOXON CORRECT=NO;
CLASS SMOK;
VAR NICOT_ADDICT;
RUN;코드는 두 군에서의 비모수 중앙값 검정인 맨 휘트니 U 검정과 같다.(2022.12.20 - [모평균 검정/SAS] - [SAS] 윌콕슨 순위 합 검정, 맨 휘트니 U 검정 (비모수 독립 표본 중앙값 검정: Wilcoxon rank sum test, Mann-Whitney U test) - NPAR1WAY())
PROC NPAR1WAY DATA=hong.df WILCOXON CORRECT=NO; : 비모수 검정을 시행한다. 데이터는 hong라이브러리의 df를 사용하고, 크루스칼 왈리스 검정을 시행한다. 연속성 수정은 하지 않는다.(연속성 수정에 관한 내용은 다음 링크를 확인하길 바란다.2022.08.30 - [통계 이론] - [이론] 연속성을 수정한 카이 제곱 검정 (Chi-squared test with Yates's correction for continuity))
CLASS SMOK; : SMOK값에 따라 검정을 시행한다. (흡연 여부에 따라 시행한다.)
VAR NICOT_ADDICT; : NICOT_ADDICT값을 검정한다.
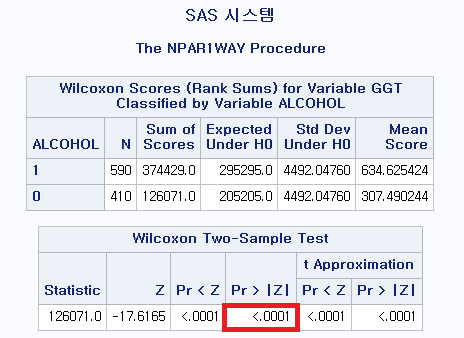
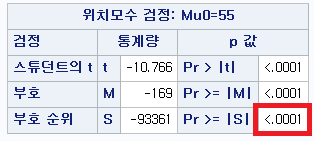
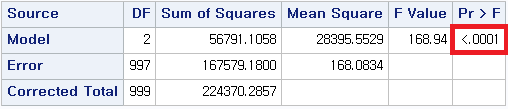
결과
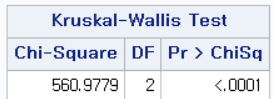
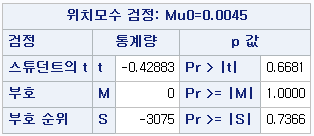
P-value가 <0.0001이므로 귀무가설을 기각하고 대립 가설을 채택한다. 그렇다면 여기에서 귀무가설 및 대립 가설은 무엇이었는가?
귀무가설: $H_0=$ 세 집단의 모평균은 "모두" 동일하다.
대립 가설: $H_1=$ 세 집단의 모평균이 모두 동일한 것은 아니다.
우리는 대립 가설을 채택해야 하므로 "세 집단의 모평균이 모두 동일한 것은 아니다."라고 결론 내릴 것이다.
이 말은, 세 집단 중 두 개씩 골라 비교했을 때, 적어도 한 쌍에서는 차이가 난다는 것이다. 따라서 세 집단 중 두 개씩 골라 비교를 해보아야 하며, 이를 사후 분석 (post hoc analysis)이라고 한다. 세 집단에서 두 개씩 고르므로 가능한 경우의 수는 $_3 C_2 =3$이다.
(1) 비흡연자 vs 과거 흡연자
(2) 비흡연자 vs 현재 흡연자
(3) 과거 흡연자 vs 현재 흡연자
비모수 검정인 Kruskal Wallis 검정의 사후 분석으로 쓰이는 방법은 다음 네 가지가 있다.
1) Pairwise Wilcoxon Test
- 가장 적절하지 않다. 왜냐하면 Kruskal wallis 검정은 기본적으로 순위를 이용한 검정 방법인데, 전체 집단에서 특정 피험자의 순위는 부분 집단에서의 순위와 다르기 때문이다. 예를 들어 전체 집단에서 흡연자인 어떤 피험자의 니코틴 중독 점수의 순위는 (비흡연자 + 현재 흡연자) 집단에서의 순위와 크게 달라진다. 동시에 분산도 크게 달라지기 때문에 적절하지 않다.
2) Conover Test
- 상기 문제점을 해결하였고, t 분포에 근거해 판단한다.
3) Dunn Test
- 상기 문제점을 해결하였고, z 분포에 근거해 판단한다.
4) Nemenyi Test
하지만 SAS는 위 네 개 중 하나의 방법이 아닌 다른 방법을 사용한다.
Dwass, Steel, Critchlow-Fligner (DSCF) multiple comparison procedure를 사용하며 이는 pairwise Wilcoxon test를 기반으로 하나, 특수한 방법으로 그 familywise error rate를 보정하고 있다. 이 방법은 Conover Test보다 더 우수한 것으로 받아들여지고 있다.
DSCF 사후 검정 - 코드
PROC NPAR1WAY DATA=hong.df WILCOXON DSCF CORRECT=NO;
CLASS SMOK;
VAR NICOT_ADDICT;
RUN;일반적인 Kruskal Wallis 검정을 시행하되, 첫 번째 줄에 "DSCF"를 추가해 준 것이 끝이다.
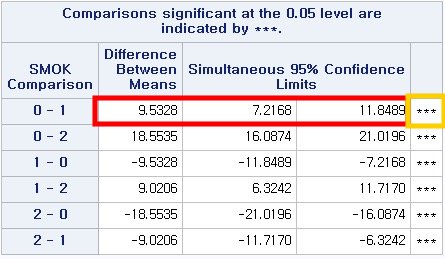
결과
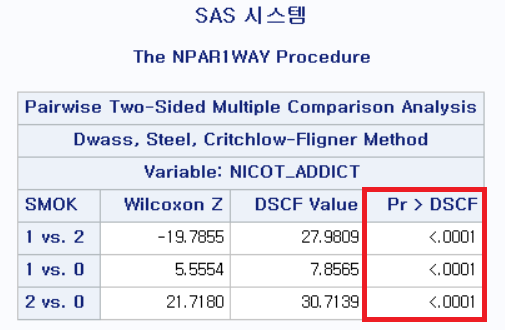
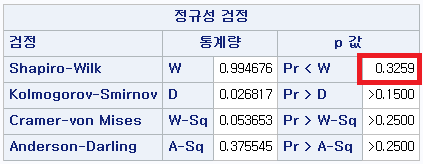
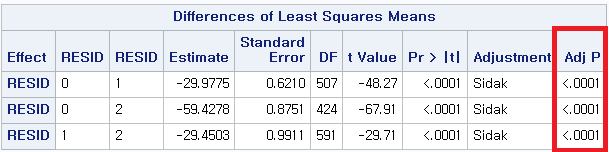
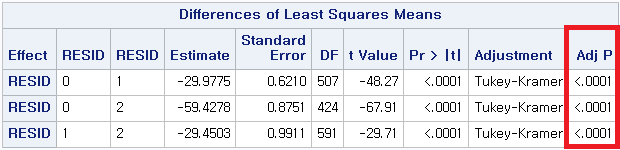
여러 값이 제시되지만, 마지막 열인 "Pr>DSCF"인 p-value만 보면 된다.
(1) 과거 흡연자(SMOK=1) vs 현재 흡연자 (SMOK=2) : p-value < 0.0001
(2) 과거 흡연자 (SMOK=1) vs 비흡연자 (SMOK=0) : p-value < 0.0001
(3) 현재 흡연자 (SMOK=2) vs 비흡연자 (SMOK=0) : p-value < 0.0001
모든 p-value가 0.05보다 작으므로 다음과 같이 결론 내릴 수 있다.
비흡연자 (0)와 과거 흡연자 (1) 사이에는 NICOT_ADDICT 중앙값에 차이가 있다.
비흡연자 (0)와 현재 흡연자 (2) 사이에는 NICOT_ADDICT 중앙값에 차이가 있다.
과거 흡연자 (1)와 현재 흡연자 (2)) 사이에는 NICOT_ADDICT 중앙값에 차이가 있다.
어떤 사후 분석을 쓸 것인가
이 논의에 대해 정답이 따로 있는 것은 아니다. 적절한 방법을 사용하여 논문에 제시하면 되고, 어떤 것이 정답이라고 콕 집어 이야기할 수는 없다. 다만, 사후 분석 방법이 여러 가지가 있다는 것은 '사후 분석 방법에 따라 산출되는 결과가 달라질 수 있다.'는 것을 의미하고, 심지어는 '어떤 사후 분석 방법을 채택하냐에 따라 유의성 여부가 달라질 수도 있다.'는 것을 의미한다. 심지어, Kruskal-Wallis test에서는 유의한 결과가 나왔는데, 사후 분석을 해보니 유의한 차이를 보이는 경우가 없을 수도 있다. 따라서 어떤 사후 분석 방법 결과에 따른 결과인지 유의하여 해석할 필요가 있다.
왜 굳이 Kruskal Wallis test를 쓰는 것인가?
이 시점에서 이런 의문이 들 수 있다.
"각각의 그룹별로 평균을 비교하면 되지, 굳이 왜 Kruskal Wallis test라는 방법까지 사용하는 것인가?"
아주 논리적인 의문점이다. 하지만, 반드시 Kruskal-Wallis test를 사용해야 한다. 그 이유는 다음과 같다. 본 사례는 흡연 상태에 따른 조합 가능한 경우의 수가 3인데, 각각 유의성의 기준을 $\alpha=0.05$로 잡아보자. 이때 세 번의 비교에서 모두 귀무가설이 학문적인 진실인데(평균에 차이가 없다.), 세 번 모두 귀무가설을 선택할 확률은 $\left( 1-0.05 \right)^3 \approx 0.86$이다. (이해가 어려우면 p-value에 대한 설명 글을 읽고 오길 바란다. 2022.09.05 - [통계 이론] - [이론] p-value에 관한 고찰)
그런데, Kruskal-Wallis test의 귀무가설은 "모든 집단의 중앙값이 같다."이다. 따라서 모든 집단의 중앙값이 같은 것이 학문적 진실일 때, 적어도 한 번이라도 대립 가설을 선택하게 될 확률은 $1-0.86=0.14$가 된다. 즉, 유의성의 기준이 올라가게 되어, 덜 보수적인 결정을 내리게 되고, 다시 말하면 대립 가설을 잘 선택하는 쪽으로 편향되게 된다. 학문적으로는 '다중 검정 (multiple testing)을 시행하면 1종 오류가 발생할 확률이 증가하게 된다.'라고 표현한다.
따라서, 각각을 비교해 보는 것이 아니라 한꺼번에 비교하는 Kruskal-Wallis test를 시행해야 함이 마땅하다.
여기에서 한 번 더 의문이 들 수 있다.
"사후 분석을 할 때에는 1종 오류가 발생하지 않는가?"
그렇다. 1종 오류가 발생할 확률이 있으므로, p-value의 기준을 더 엄격하게 (0.05보다 더 작게) 잡아야 한다. P-value를 보정하는 방법은 일반적으로는 Bonferroni, holm, hochberg, hommel, BH, BY, FDR 등이 있고, Kruskal-Wallis test의 사후 분석 방법으로는 특별히 Pairwise Wilcoxon Test, Conover Test, Dunn Test, Nemenyi Test, DSCF을 사용하고 있다.
코드 정리
*라이브러리 지정하기;
LIBNAME hong "C:/Users/User/Documents/Tistory_blog";
*파일 불러오기;
PROC IMPORT
DATAFILE="C:\Users\user\Documents\Tistory_blog\Data.xlsx"
DBMS=EXCEL
OUT=hong.df
REPLACE;
RUN;
*정규성 검정하기;
PROC UNIVARIATE DATA=hong.df NORMAL PLOT;
CLASS SMOK;
VAR NICOT_ADDICT;
HISTOGRAM NICOT_ADDICT/ NORMAL (MU=EST SIGMA=EST);
RUN;
*크루스칼 왈리스 검정;
PROC NPAR1WAY DATA=hong.df WILCOXON CORRECT=NO;
CLASS SMOK;
VAR NICOT_ADDICT;
RUN;
*크루스칼 왈리스 검정 & 사후검정;
PROC NPAR1WAY DATA=hong.df WILCOXON DSCF CORRECT=NO;
CLASS SMOK;
VAR NICOT_ADDICT;
RUN;[SAS] 크루스칼 왈리스 검정 (비모수 일원 배치 분산 분석: Kruskal-Wallis Test) 정복 완료!
작성일: 2023.04.05.
최종 수정일: 2023.04.05.
이용 프로그램: SAS v9.4
운영체제: Windows 11