
[SAS] 등분산 가정이 성립하지 않는 일원 배치 분산 분석 (Welch's ANOVA) - PROC GLM, PROC MIXED
이전 포스팅에서 흡연 상태를 "1) 비흡연자", "2) 과거 흡연자", "3) 현재 흡연자"로 나누었고, 각 그룹의 폐기능 검사 중 하나인 FVC (Forced Vital Capacity)의 평균에 차이가 있는지 알아보고자 하여 일원 배치 분산 분석 (ANOVA)를 시행하였다. 2022.10.12 - [모평균 검정/SAS] - [SAS] 일원 배치 분산 분석 (One-way ANOVA, ANalysis Of VAriance) - PROC GLM, PROC ANOVA
ANOVA의 전제 조건은 두 가지였다.
1) 정규성
2) 등분산성
만약 '1) 정규성'은 만족하지만 '2) 등분산성'이 성립하지 않는 경우에는 어떻게 해야 할까?
당연히, 이전 포스팅의 일반적인 ANOVA는 실시할 수 없고, Welch's ANOVA를 시행해야 한다.
이번 포스팅에서는 이 Welch's ANOVA를 다뤄보고자 한다.
*실습용 데이터는 아래 링크를 클릭하면 다운로드할 수 있습니다.
2022.08.04 - [공지사항 및 소개] - 분석용 데이터 (update 22.11.26)
분석용 데이터 (update 22.11.26)
2022년 11월 26일 버전입니다. 변수는 계속하여 추가될 예정입니다. 다음 카테고리에 있는 글에서 이용된 데이터입니다. - 기술 통계 - 범주형 자료 분석 - 모평균 검정 - 반복 측정 자료 분석 - 통계
medistat.tistory.com
시작하기 위해 라이브러리를 만들고, 파일을 불러온다.
라이브러리 만드는 방법: 2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 라이브러리 만들기 - LIBNAME
파일 불러오는 방법: 2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 데이터 불러오기 및 저장하기 - PROC IMPORT, PROC EXPORT
*라이브러리 지정하기;
LIBNAME hong "C:/Users/User/Documents/Tistory_blog";
*파일 불러오기;
PROC IMPORT
DATAFILE="C:\Users\user\Documents\Tistory_blog\Data.xlsx"
DBMS=EXCEL
OUT=hong.df
REPLACE;
RUN;
목표: 거주 지역 단위에 따라 삶의 질의 평균이 모집단 수준에서 서로 다르다고 말할 수 있는가?
전제조건 (정규성)
Welch's ANOVA에는 하나의 전제조건이 필요하다. 본 포스팅의 예시에 맞추어 설명하면 다음과 같다.
1) 정규성: 대도시, 중소도시, 시골 거주자 별로 삶의 질의 분포를 보았을 때 각각의 분포는 정규성을 따른다.
그리고, 분산은 같지 않아도 된다.
1) 정규성
정규성 검정에 관한 내용은 다음 링크에서 확인할 수 있다.
2022.08.12 - [기술 통계/SAS] - [SAS] 정규성 검정 - PROC UNIVARIATE
PROC UNIVARIATE DATA=hong.df NORMAL PLOT;
CLASS RESID;
VAR QOL;
HISTOGRAM QOL/ NORMAL (MU=EST SIGMA=EST);
RUN;
결과
1) 대도시 거주자 (RESID=0)
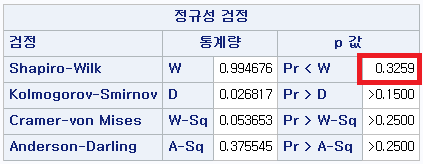
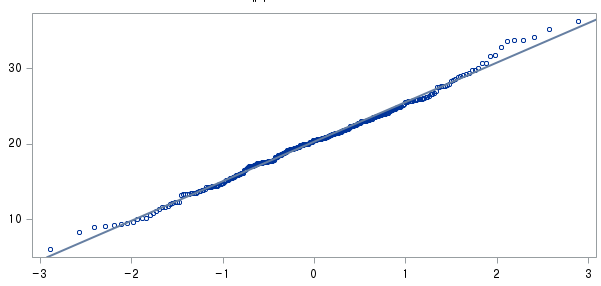

표본의 수가 2,000이 되지 않으므로 Shapiro-Wilk 통계량의 p-value를 보아야 하고, 이는 0.05보다 크다. Q-Q plot, 히스토그램에서 정규성을 띠지 않는다고 할만한 근거가 없으므로 정규성을 따른다고 결론을 짓는다.
2) 중소도시 거주자 (RESID=1)
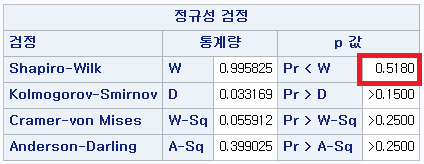
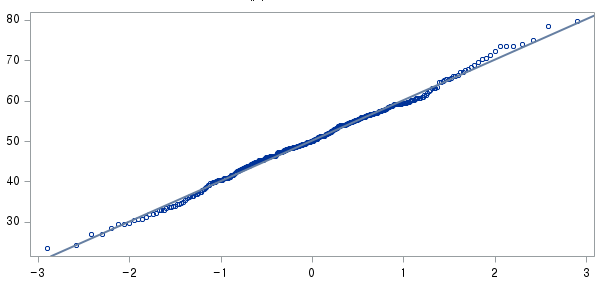
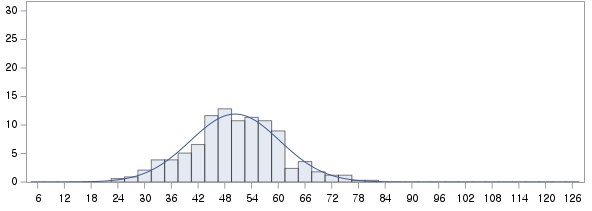
표본의 수가 2,000이 되지 않으므로 Shapiro-Wilk 통계량의 p-value를 보아야 하고, 이는 0.05보다 크다. Q-Q plot, 히스토그램에서 정규성을 띠지 않는다고 할만한 근거가 없으므로 정규성을 따른다고 결론을 짓는다.
3) 시골 거주자 (RESID=2)
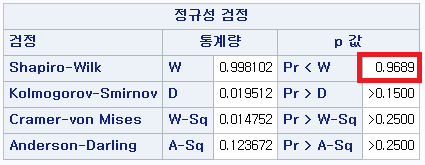
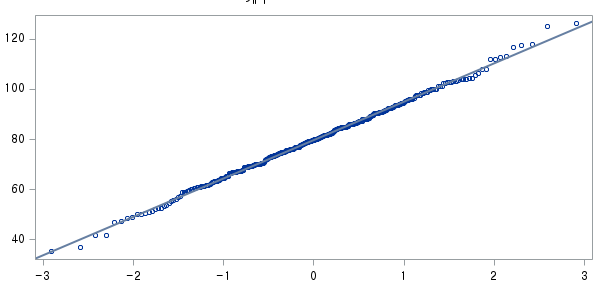
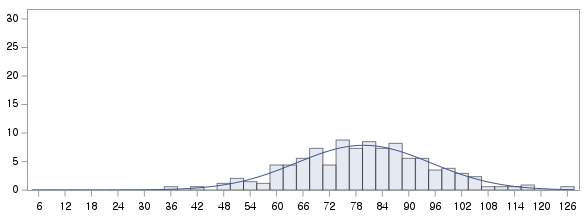
표본의 수가 2,000이 되지 않으므로 Shapiro-Wilk 통계량의 p-value를 보아야 하고, 이는 0.05보다 크다. Q-Q plot, 히스토그램에서 정규성을 띠지 않는다고 할만한 근거가 없으므로 정규성을 따른다고 결론을 짓는다.
따라서 정규성 전제는 따른다고 할 수 있다.
2) 등분산성
분산이 같은지 확인해보도록 하겠다.
등분산성 검정에 관한 내용은 다음 링크에서 확인할 수 있다.
2022.10.04 - [모평균 검정/SAS] - [SAS] 독립 표본 T검정 (Independent samples T-test) - PROC TTEST
2022.10.05 - [모평균 검정/SAS] - [SAS] 등분산성 검정 (Homogeneity of variance) - PROC GLM
위 두 개 글에서 제시한 네 가지 방법 모두를 사용하여 등분산 검정을 시행해 보겠다.
*1) Levene;
PROC GLM DATA=hong.df;
CLASS RESID;
MODEL QOL=RESID;
MEANS RESID/ HOVTEST=LEVENE(TYPE=ABS);
RUN;
*2) O'Brien;
PROC GLM DATA=hong.df;
CLASS RESID;
MODEL QOL=RESID;
MEANS RESID/ HOVTEST=OBRIEN;
RUN;
*3) Brwon and Forsythe;
PROC GLM DATA=hong.df;
CLASS RESID;
MODEL QOL=RESID;
MEANS RESID/ HOVTEST=BF;
RUN;
*4) Bartlett;
PROC GLM DATA=hong.df;
CLASS RESID;
MODEL QOL=RESID;
MEANS RESID/ HOVTEST=BARTLETT;
RUN;
QUIT;
결과
1) Levene
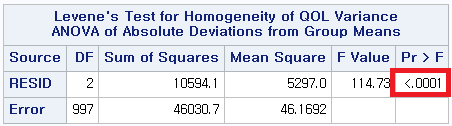
2) O'Brien
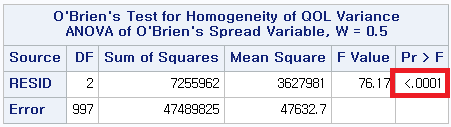
3) Brown and Forsythe
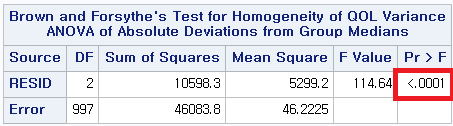
4) Bartlett

어떤 방법을 사용하더라도 p-value<0.0001로 등분산성은 만족하지 않는다는 것을 알 수 있다. 따라서 일원 배치 분산 분석 (One-way ANOVA)이 아닌 Welch's ANOVA를 시행해야 한다.
Welch's 일원 배치 분산 분석 (Welch's One way ANOVA) 코드
PROC GLM DATA=hong.df;
CLASS RESID;
MODEL QOL=RESID;
MEANS RESID/ WELCH;
RUN;
QUIT;PROC GLM DATA=hong.df; : Welch's ANOVA를 시행할 수 있는 PROC GLM으로 코드를 시작한다. 데이터는 hong 라이브러리의 df데이터를 활용한다.
CLASS RESID; : RESID에 따른 평균을 비교할 것이다.
MODEL QOL=RESID; : RESID에 따른 QOL의 평균을 비교할 것이다.
MEANS RESID/ WELCH; : RESID의 평균을 보여주고, Welch's ANOVA를 추가로 시행하라.
결과

P-value가 <0.0001이므로 귀무가설을 기각하고 대립 가설을 채택한다. 그렇다면 여기에서 귀무가설 및 대립 가설은 무엇이었는가?
귀무가설: $H0=$ 세 집단의 모평균은 "모두" 동일하다.
대립 가설: $H1=$ 세 집단의 모평균이 모두 동일한 것은 아니다.
우리는 대립 가설을 채택해야 하므로 "세 집단의 모평균이 모두 동일한 것은 아니다."라고 결론 내릴 것이다.
이 말은, 세 집단 중 두 개씩 골라 비교했을 때, 적어도 한 쌍에서는 차이가 난다는 것이다. 따라서 세 집단 중 두 개씩 골라 비교를 해보아야 하며, 이를 사후 분석 (post hoc analysis)이라고 한다. 세 집단에서 두 개씩 고르므로 가능한 경우의 수는 $_3 C_2=3$이다.
(1) 대도시 거주자 vs 중소도시 거주자
(2) 대도시 거주자 vs 시골 거주자
(3) 중소도시 거주자 vs 시골 거주자
사후 분석을 시행할 것이다.
이전 일반 ANOVA 포스팅(2022.10.12 - [모평균 검정/SAS] - [SAS] 일원 배치 분산 분석 (One-way ANOVA, ANalysis Of VAriance) - PROC GLM, PROC ANOVA)에서는 많은 사후 분석 방법이 있다고 소개했었다. 하지만 등분산이 가정되지 않는 상황에서 쓸 수 있는 사후 분석 방법은 현저히 적어진다. 많이들 쓰는 방법은 다음 네 가지다.
1) Tamhane's T2
2) Games-Howell
3) Dunnett's T3
4) Dunnett's C
하지만 마지막 Dunnett's C는 SAS에서 제공하지 않으므로 위 세 가지 방법에 대해서만 알아보도록 하겠다.
사후 분석 코드
*1) Tamhane's T2;
PROC MIXED DATA=hong.df;
CLASS RESID;
MODEL QOL=RESID/DDFM=SATTERTH;
REPEATED/GROUP=RESID;
LSMEANS RESID/ADJUST=SIDAK ADJDFE=ROW;
RUN;
*2) Games-Howell;
PROC MIXED DATA=hong.df;
CLASS RESID;
MODEL QOL=RESID/DDFM=SATTERTH;
REPEATED/GROUP=RESID;
LSMEANS RESID/ADJUST=TUKEY ADJDFE=ROW;
RUN;
*3) Dunnett's T3;
PROC MIXED DATA=hong.df;
CLASS RESID;
MODEL QOL=RESID/DDFM=SATTERTH;
REPEATED/GROUP=RESID;
LSMEANS RESID/ADJUST=SMM ADJDFE=ROW;
RUN;PROC MIXED DATA=hong.df; : 사후 분석을 시행하는 PROC MIXED로 시작하고, 데이터는 hong 라이브러리의 df 데이터를 사용한다.
CLASS RESID; : RESID에 따라 사후 분석을 시행한다.
MODEL QOL=RESID/DDFM=SATTERTH; : RESID에 따른 QOL 평균의 비교를 한다. (DDFM=SATTERTH는 자유도를 근사시킬 때 사용하는 옵션이다.)
REPEATED/GROUP=RESID; : 이는 R matrix 추정에 관한 내용이다.
LSMEANS RESID/ADJUST=SIDAK ADJDFE=ROW; : "ADJUST=SIDAK"과 "ADJDFE=ROW"의 조합은 Tamhane's T2 사후 검정을 하도록 지시한다.
"ADJUST="에 "TUKEY"를 넣으면 Games-Howell, "SMM"을 넣으면 Dunnett's T3검정을 시행한다.
1) Tamhane's T2
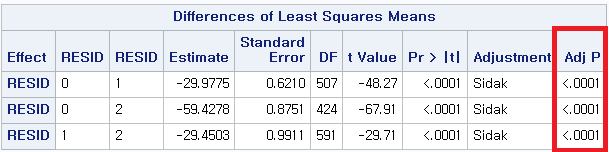
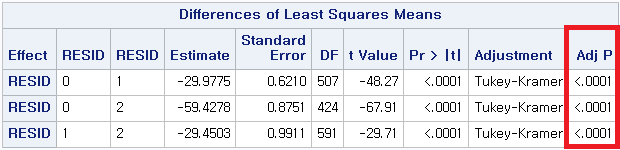
2) Games-Howell
3) Dunnett's T3
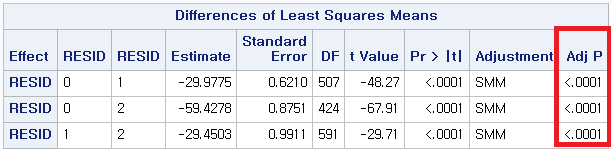
봐야 할 것은 "Adj P", 즉 보정된 p-value이다. 방법에 관계없이 p-value는 모두 0.0001보다 작다. 따라서 다음과 같이 결론 내릴 수 있다.
대도시 거주자 (0)과 중소도시 거주자 (1) 사이에는 QOL 평균에 차이가 있다.
대도시 거주자 (0)과 시골 거주자 (2) 사이에는 QOL 평균에 차이가 있다.
중소도시 거주자 (1)과 시골 거주자 (2) 사이에는 QOL 평균에 차이가 있다.
어떤 사후 분석을 쓸 것인가
이 논의에 대해 정답이 따로 있는 것은 아니다. 적절한 방법을 사용하여 논문에 제시하면 되고, 어떤 것이 정답이라고 콕 집어 이야기할 수는 없다. 다만, 사후 분석 방법이 여러 가지가 있다는 것은 '사후 분석 방법에 따라 산출되는 결과가 달라질 수 있다.'는 것을 의미하고, 심지어는 '어떤 사후 분석 방법을 채택하냐에 따라 유의성 여부가 달라질 수도 있다.'는 것을 의미한다. 심지어, Welch's ANOVA에서는 유의한 결과가 나왔는데, 사후 분석을 해보니 유의한 차이를 보이는 경우가 없을 수도 있다. 따라서 어떤 사후 분석 방법 결과에 따른 결과인지 유의하여 해석할 필요가 있다.
코드 정리
*라이브러리 지정하기;
LIBNAME hong "C:/Users/User/Documents/Tistory_blog";
*파일 불러오기;
PROC IMPORT
DATAFILE="C:\Users\user\Documents\Tistory_blog\Data.xlsx"
DBMS=EXCEL
OUT=hong.df
REPLACE;
RUN;
*정규성 검정하기;
PROC UNIVARIATE DATA=hong.df NORMAL PLOT;
CLASS RESID;
VAR QOL;
HISTOGRAM QOL/ NORMAL (MU=EST SIGMA=EST);
RUN;
*등분산성 검정하기;
*1) Levene;
PROC GLM DATA=hong.df;
CLASS RESID;
MODEL QOL=RESID;
MEANS RESID/ HOVTEST=LEVENE(TYPE=ABS);
RUN;
*2) O'Brien;
PROC GLM DATA=hong.df;
CLASS RESID;
MODEL QOL=RESID;
MEANS RESID/ HOVTEST=OBRIEN;
RUN;
*3) Brwon and Forsythe;
PROC GLM DATA=hong.df;
CLASS RESID;
MODEL QOL=RESID;
MEANS RESID/ HOVTEST=BF;
RUN;
*4) Bartlett;
PROC GLM DATA=hong.df;
CLASS RESID;
MODEL QOL=RESID;
MEANS RESID/ HOVTEST=BARTLETT;
RUN;
QUIT;
*Welch's ANOVA 시행하기;
PROC GLM DATA=hong.df;
CLASS RESID;
MODEL QOL=RESID;
MEANS RESID/ WELCH;
RUN;
QUIT;
*사후분석 시행하기;
*1) Tamhane's T2;
PROC MIXED DATA=hong.df;
CLASS RESID;
MODEL QOL=RESID/DDFM=SATTERTH;
REPEATED/GROUP=RESID;
LSMEANS RESID/ADJUST=SIDAK ADJDFE=ROW;
RUN;
*2) Games-Howell;
PROC MIXED DATA=hong.df;
CLASS RESID;
MODEL QOL=RESID/DDFM=SATTERTH;
REPEATED/GROUP=RESID;
LSMEANS RESID/ADJUST=TUKEY ADJDFE=ROW;
RUN;
*3) Dunnett's T3;
PROC MIXED DATA=hong.df;
CLASS RESID;
MODEL QOL=RESID/DDFM=SATTERTH;
REPEATED/GROUP=RESID;
LSMEANS RESID/ADJUST=SMM ADJDFE=ROW;
RUN;
사실 등분산성이 만족하지 않을 때 시행할 수 있는 ANOVA로 Welch's ANOVA 외에도 Brown and Forsythe ANOVA가 있다. 이것과 Dunnett's C 사후 검정을 SPSS에서는 시행할 수 있으므로 필요한 경우 SPSS에서 시행해볼 수도 있겠다.
[SAS] 등분산 가정이 성립하지 않는 일원 배치 분산 분석 (Welch's ANOVA) 정복 완료!
작성일: 2022.11.26.
최종 수정일: 2022.11.26.
이용 프로그램: SAS v9.4
운영체제: Windows 10