
[SAS] 윌콕슨 순위 합 검정, 맨 휘트니 U 검정 (비모수 독립 표본 중앙값 검정: Wilcoxon rank sum test, Mann-Whitney U test) - NPAR1WAY()
두 분포의 평균이 다른지 확인하는 방법을 이전에는 독립 표본 T검정 (Two-Sample T test)로 시행했었다. (2022.10.04 - [모평균 검정/SAS] - [SAS] 독립 표본 T검정 (Independent samples T-test) - PROC TTEST) 하지만 여기에는 중요한 가정이 필요한데, 각각의 분포가 정규성을 따르는 것이다. 하지만 분포가 정규성을 따르지 않는다면 어떻게 해야 할까? 그럴 때 사용하는 것이 Wilcoxon rank sum test (윌콕슨 순위 합 검정)이다. 윌콕슨 순위 합 검정 (Wilcoxon rank sum test)는 이후에 Mann과 Whitney가 개정을 하였고 그때 U 통계량을 사용하므로 맨 휘트니 U 검정(Mann-Whitney U test)이라고도 한다. 또한 세 사람의 이름을 붙여 Wilcoxon-Mann-Whitney Test (WMW test)라고도 한다.
이번 포스팅에서는 윌콕슨 순위 합 검정 (Wilcoxon rank sum test)에 대해 알아볼 것이다.
*실습용 데이터는 아래 링크를 클릭하면 다운로드할 수 있습니다.
2022.08.04 - [공지사항 및 소개] - 분석용 데이터 (update 22.12.18)
분석용 데이터 (update 22.12.18)
2022년 12월 18일 버전입니다. 변수는 계속하여 추가될 예정입니다. 다음 카테고리에 있는 글에서 이용된 데이터입니다. - 기술 통계 - 범주형 자료 분석 - 모평균 검정 - 상관분석 - 반복 측정 자료
medistat.tistory.com
시작하기 위해 라이브러리를 만들고, 파일을 불러온다.
라이브러리 만드는 방법: 2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 라이브러리 만들기 - LIBNAME
파일 불러오는 방법: 2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 데이터 불러오기 및 저장하기 - PROC IMPORT, PROC EXPORT
*라이브러리 지정하기;
LIBNAME hong "C:/Users/User/Documents/Tistory_blog";
*파일 불러오기;
PROC IMPORT
DATAFILE="C:\Users\user\Documents\Tistory_blog\Data.xlsx"
DBMS=EXCEL
OUT=hong.df
REPLACE;
RUN;
목표: 음주 여부에 따라 Gamma-glutamyl transferase(GGT)의 중앙값이 모집단 수준에서 서로 다르다고 말할 수 있는가?
정규성 - 코드
만약 GGT의 분포가 정규성을 따른다면, 독립 표본 T 검정으로 이를 확인할 수 있을 것이다. 독립 표본 (Indepent samples, Two tamples) T 검정의 전제조건은 각각의 독립 표본의 분포가 정규성을 따른다는 것이다. 즉, 여기에서는 음주 여부에 따라 GGT의 정규성을 검정하도록 하겠다.
- 정규성 검정에 관한 분석 내용은 다음 글에서 살펴볼 수 있다. 2022.08.12 - [기술 통계/SAS] - [SAS] 정규성 검정 - PROC UNIVARIATE
- PROC UNIVARIATE명령문에서 "CLASS"옵션을 사용하는 방법은 다음 글에서 살펴볼 수 있다. 2022.09.23 - [기술 통계/SAS] - [SAS] 기술 통계 (평균, 표준편차, 표준오차, 최댓값, 최솟값, 중위수, 분위수 등) - PROC UNIVARIATE, PROC MEANS
PROC UNIVARIATE DATA=hong.df NORMAL PLOT;
CLASS ALCOHOL;
VAR GGT;
HISTOGRAM GGT/ NORMAL (MU=EST SIGMA=EST);
RUN;
정규성 검정 - 결과
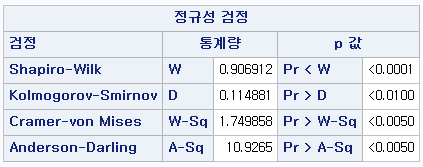
1) ALCOHOL=0 (비음주자 군)
2) ALCOHOL=1 (음주자 군)
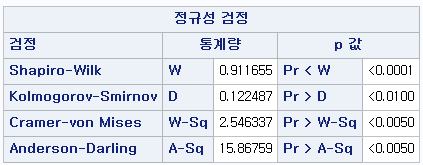
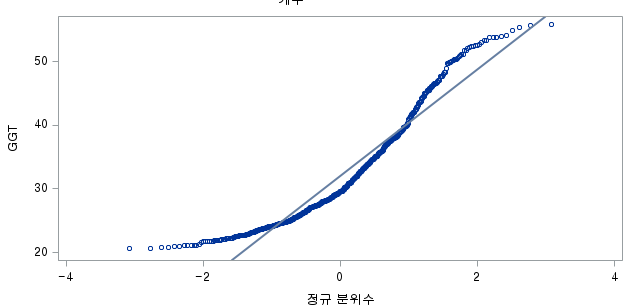
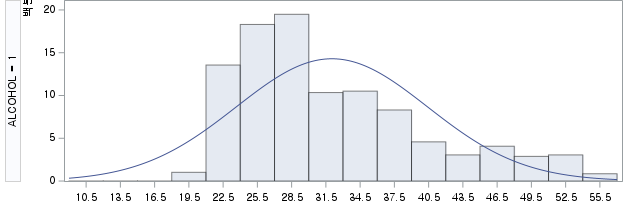
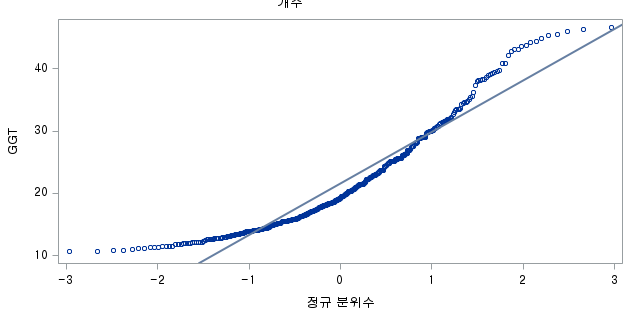
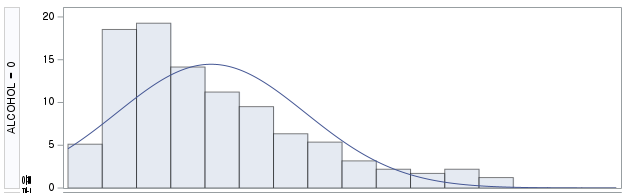
N수가 2,000개 미만이므로 Shapiro-Wilk 통계량의 p-value를 보면 0.05 이하이며, Q-Q Plot은 대부분의 데이터가 선상에 있지 않고, 히스토그램에서도 정규성을 따르지 않는 것처럼 보인다. 따라서 독립 표본 T검정 (Two-sample T-test)를 시행할 수 없고, 맨 휘트니 U 검정 (Mann-Whitney U test)을 시행해야 한다.
맨 휘트니 U 검정 (Mann-Whitney U test) 코드
PROC NPAR1WAY DATA=hong.df WILCOXON CORRECT=NO;
CLASS ALCOHOL;
VAR GGT;
RUN;PROC NPAR1WAY DATA=hong.df WILCOXON CORRECT=NO; : 비모수 검정을 시행한다. 데이터는 hong라이브러리의 df를 사용하고, 윌콕슨 검정 (맨 휘트니 U 검정)을 시행한다. 연속성 수정은 하지 않는다.(연속성 수정에 관한 내용은 다음 링크를 확인하길 바란다.2022.08.30 - [통계 이론] - [이론] 연속성을 수정한 카이 제곱 검정 (Chi-squared test with Yates's correction for continuity))
CLASS ALCOHOL; : ALCOHOL값에 따라 검정을 시행한다. (음주 여부에 따라 시행한다.)
VAR GGT; : GGT값을 검정한다.
*만약 연속성 수정을 원한다면 "CORRECT=NO"를 빼버리면 된다.
결과
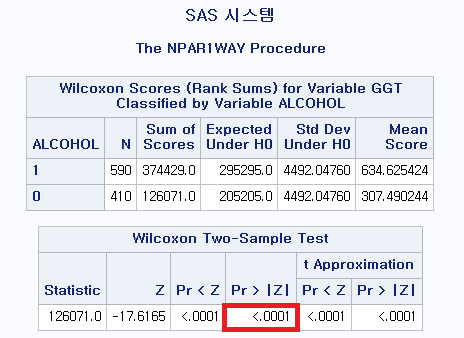
빨간 박스 안 양측 검정 p-value가 매우 작으므로 유의한 결과임을 알 수 있다. 따라서 귀무가설을 기각하고 대립 가설을 택해야 한다. 여기에서 귀무가설과 대립 가설은 무엇일까?
귀무가설 $H_0=$ 두 분포는 동일하다.
대립 가설$H_1=$ 두 분포는 평균만 다를 뿐, 분포는 똑같이 생겼다.
즉, 대립 가설이 의미하는 것은 두 분포는 평행이동 관계에 있다는 것이다. 그래야 중앙값이 달라진 것인지 확인할 수 있다.
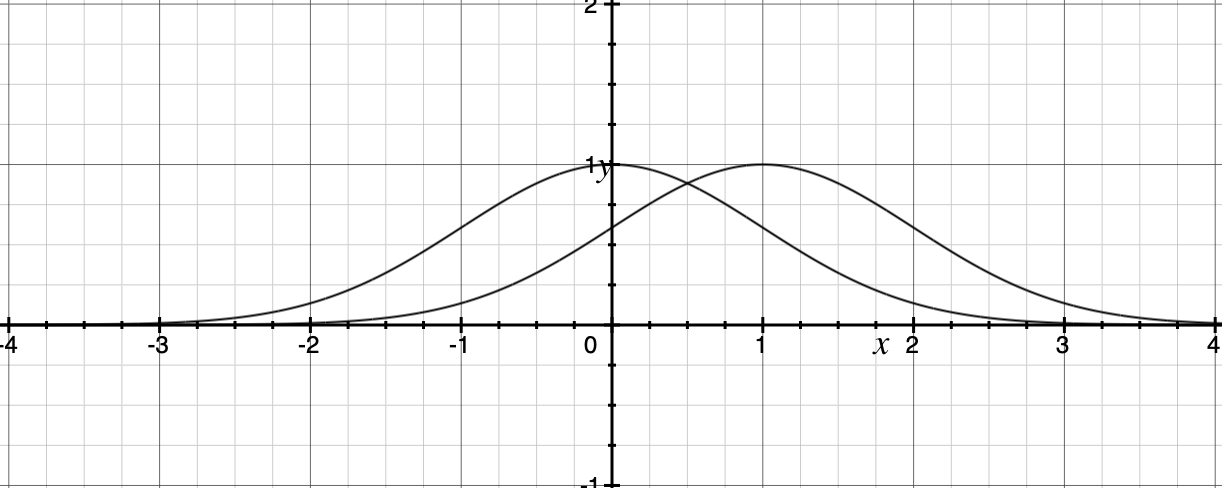
이 말은, 맨 휘트니 U 검정에도 필요한 가정이 있다는 말이다. 두 분포는 동일하게 생겼어야 한다.
조금 어렵게 이야기하면, 두 분포의 first moment는 다르지만, 그보다 고차원의 central moment는 같아야 한다.
만약 생김새가 다르면 맨 휘트니 U 검정을 사용하면 안 되고, Robuts rank order test 등을 시행해야 한다. (물론 현실에서는 이런 내용을 무시한 채 '정규성을 따르지 않으니 맨 휘트니 U 검정을 사용한다'는 연구자가 대다수다.) 이에 관한 내용은 다음 링크를 확인하길 바란다. 링크 추가 예정
그런데 위 히스토그램을 보면 음주자와 비음주자의 GGT분포는 right skewed 된 분포로 어느 정도 비슷하게 생겼다. 모든 central moment를 조사하는 것은 현실적으로 힘들지만, 2nd cental moment인 분산의 차이를 검정해보면 다음과 같음을 알 수 있다. 등분산성 검정 방법은 다음 링크를 확인하길 바란다.
2022.10.04 - [모평균 검정/SAS] - [SAS] 독립 표본 T검정 (Independent samples T-test) - PROC TTEST
2022.10.05 - [모평균 검정/SAS] - [SAS] 등분산성 검정 (Homogeneity of variance) - PROC GLM
코드
PROC TTEST DATA=hong.df;
CLASS HTN;
VAR GGT;
RUN;결과

p-value는 0.7922로 분산에 차이가 없다고 결론 내리는 것이 합당하다.
따라서 두 분포의 모양이 같다고 생각하면 본 맨 휘트니 U 검정으로 음주자와 비음주자의 GGT값에는 차이가 있다고 결론 내릴 수 있다.
만약, 분포가 다르게 생기면 어떤 결과가 초래되길래 그렇게 강조하는 걸까?
R에서 시행한 내용을 참조하면 다음과 같다.
R에서 NP3_raw는 right skewed, NP4_raw는 left skewed로 서루 매우 다르게 생겼음을 알 수 있다.
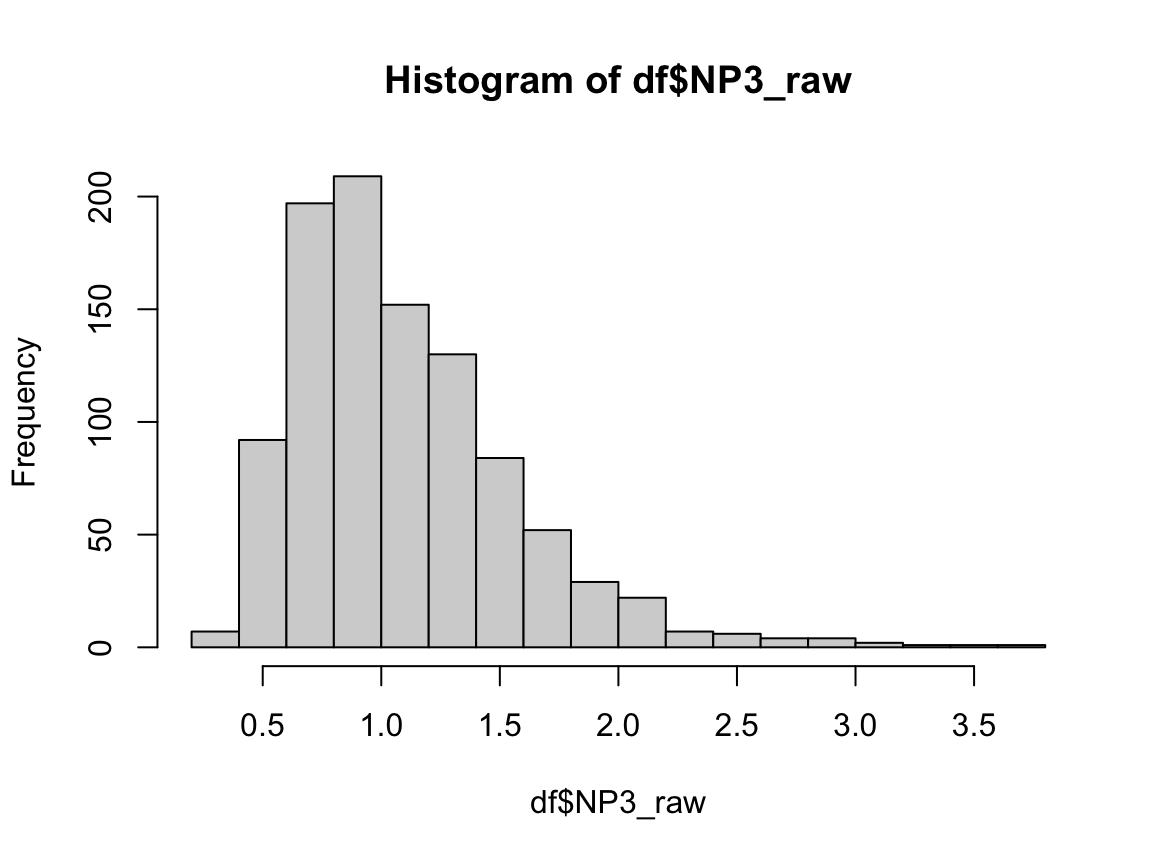
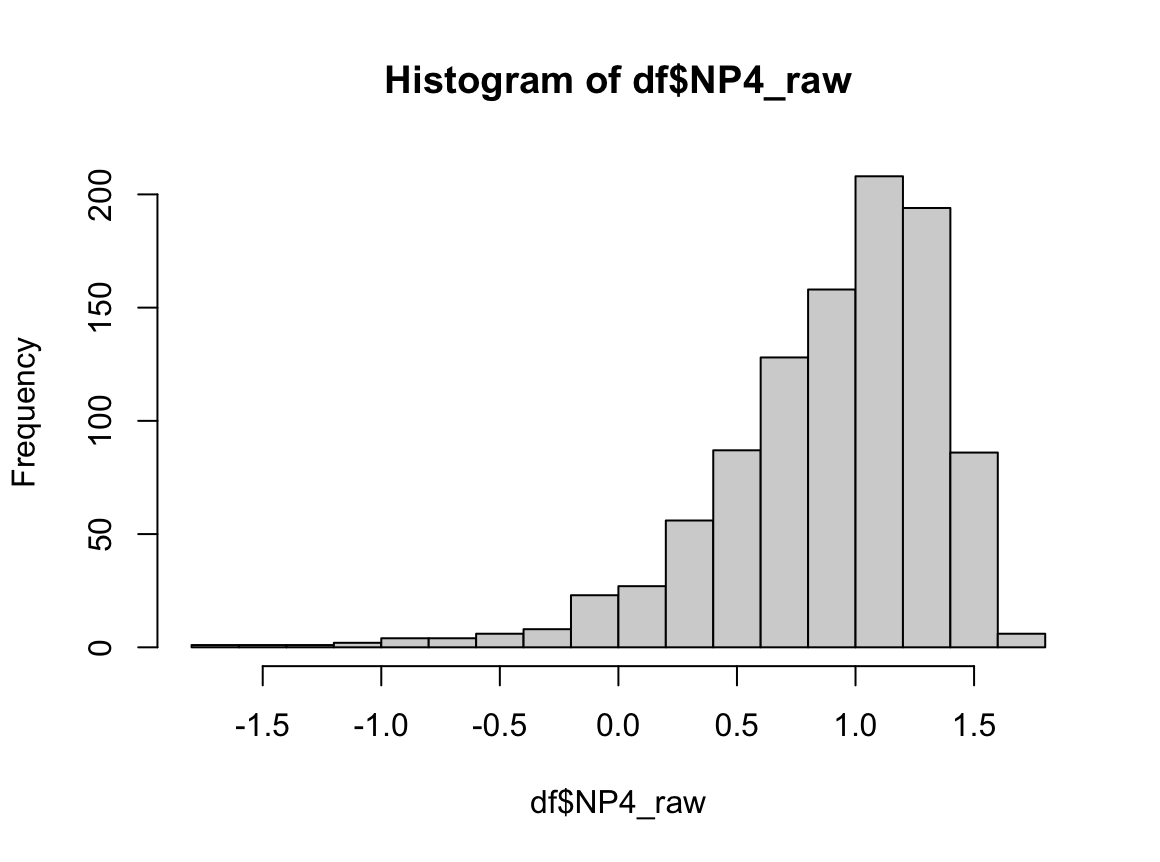
분산, 중앙값이 완벽히 일치하며, 등분산성 검정에서도 분산에 차이가 없다고 나온다. 하지만 맨 휘트니 U 검정 결과 p-value는 매우 작게 나온다. 만약 맨 휘트니 U 검정이 "중앙값이 같은지 확인하는 검정"이라고만 알고 있다면 중앙값이 완전히 같은 이런 경우에도 "중앙값에 차이가 있다."라고 결론 내릴 것이다. 하지만 이 경우 귀무가설을 기각하고 "두 분포는 다르게 생겼다."라고 결론 내려야 옳은 결론에 다다른다.
따라서 만약 생긴 모양이 같고 중앙값만 다르다면, 유의미한 맨 휘트니 U 검정의 결과는 중앙값의 차이로 귀결될 수 있다. 하지만 모양이 다르다면 중앙값의 차이로 귀결될 수 없음을 유의하길 바란다.
코드 정리
*라이브러리 지정하기;
LIBNAME hong "C:/Users/User/Documents/Tistory_blog";
*파일 불러오기;
PROC IMPORT
DATAFILE="C:\Users\user\Documents\Tistory_blog\Data.xlsx"
DBMS=EXCEL
OUT=hong.df
REPLACE;
RUN;
*정규성 검정;
PROC UNIVARIATE DATA=hong.df NORMAL PLOT;
CLASS ALCOHOL;
VAR GGT;
HISTOGRAM GGT/ NORMAL (MU=EST SIGMA=EST);
RUN;
*맨 휘트니 U 검정;
PROC NPAR1WAY DATA=hong.df WILCOXON CORRECT=NO;
CLASS ALCOHOL;
VAR GGT;
RUN;
[SAS] 윌콕슨 순위 합 검정, 맨 휘트니 U 검정 (비모수 독립 표본 중앙값 검정: Wilcoxon rank sum test, Mann-Whitney U test) 정복 완료!
작성일: 2022.12.20.
최종 수정일: 2022.12.22.
이용 프로그램: SAS v9.4
운영체제: Windows 10