
[이론] 보통최소제곱법 (Ordinary Least Squares)
의학통계를 비롯한 많은 통계에서 모수(parameter)를 추정할 때 가장 많이 쓰이는 방법 중 하나가 보통최소제곱법(Ordinary Least Squares)이다. 이에 대해 알아보고자 한다. 보통최소제곱법 (Ordinary Least Squares)은 최소제곱법 (Least Squares)와 다른 것이지만 많이들 구분하지 않고 사용하고 있다. 본 글에서는 철저히 구분하여 사용할 것이다.
최소제곱법 (Least Squares)
최소제곱법의 분류를 이해하기 위해서는 최소제곱법이 무엇인지 알아야 한다.
네 개의 표본으로부터 얻은 데이터를 다음과 같이 좌표평면 위에 표시했다고 하자.
누군가가 "이 데이터는 적절한 선형 관계로 표시할 수 있을 것 같아."라고 생각하였고, 적절한 선을 다음과 같이 그렸다고 하자.

다른 누군가는 이 직선이 아니라, 기울기와 $y$절편이 조금은 다른 직선이 더 적절하다고 주장할 수도 있다. 그렇다면 어떤 기준으로 직선을 정해야 다수가 받아들일 수 있을까? 그에 대한 답 중 하나가 최소제곱법(Least Squares)이다.
최소 제곱법은 직선 관계에서만 답을 내어줄 수 있는 것은 아니다. 또 다른 누군가는 직선이 아니라 아래와 같은 이차함수가 더 적절하다고 주장할 수 있고, 다른 누군가는 오른/왼쪽으로 조금 이동한 이차함수가 더 적절하다고 주장할 수 있다.
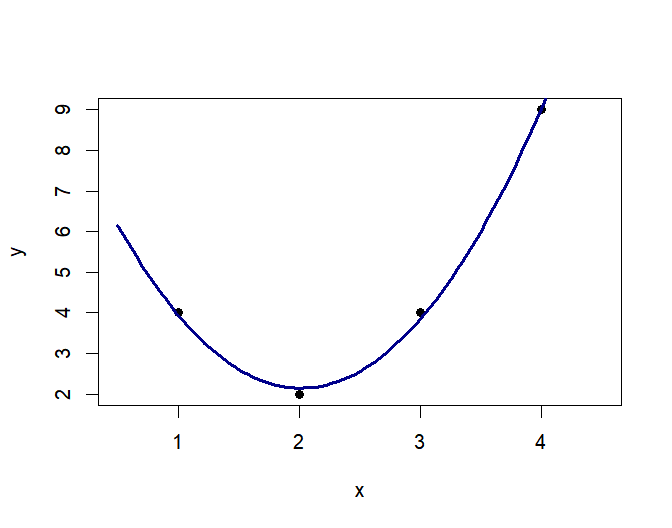
최소제곱법 (Least Squares)은 이런 문제들에 대한 답을 내어준다. 직선 관계로 표현하기로 마음먹었다면, 어떤 직선이 데이터를 가장 잘 설명하는지 답을 내어줄 수 있다. 이차 함수 관계로 표현하기로 했다면, 어떤 이차 함수가 가장 잘 설명하는지 알려줄 수 있다.
요약하면, 최소제곱법은 잔차를 제곱한 것들의 합이 최소화되는 순간을 찾는 테크닉이다. 방법은 다음과 같다.
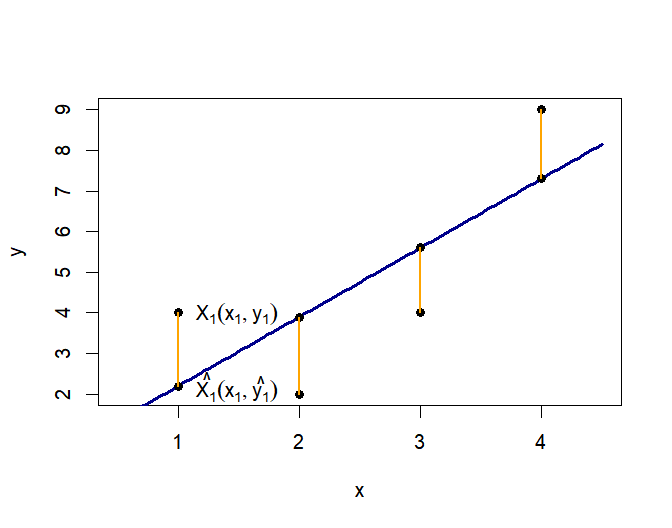
1) 데이터를 잘 설명할 것으로 예상되는 임의의 직선을 그린다.
2) 그 직선 위 $x$좌표가 데이터의 $X_1 (x_1,y_1)$의 x좌표$(x_1)$와 같은 점$(\hat{X_1})$의 $y$값$(\hat{y_1})$은 직선 관계를 사용하여 구한 예측치다.
3) 실제 $y$값$(x_1)$과 예측치$(\hat{y_1})$의 차이를 잔차라고 한다. (오렌지색 선분)
4) 오렌지색 선분들이 짧으면 짧을 수록, 직선이 데이터를 잘 설명한다고 할 수 있다. 그런 목적으로 잔차의 합을 구하면 문제가 발생한다. 데이터들은 직선 위에도, 아래에도 있으므로 잔차는 +, - 두 가지가 모두 존재한다. 따라서 단순 합산은, 오렌지색 선분이 아무리 길어도 잘 상쇄되기만 하면 0이 될 수도 있다. 그러므로 그냥 더하는 것이 아니라 제곱을 하여 더하게 된다. 이는 통계에서 분산이 편차의 합이 아닌, 편차의 제곱의 합인 이유와 같다.
5) 편차의 제곱의 합을 최소로 만드는 기울기와 $y$절편을 구하면 된다.
최소제곱법 (Least Squares)의 분류
사실 위 설명은 최소제곱법 중 하나인 보통최소제곱법 (Ordinary Least Squares, OLS)에 대한 설명이다. 최소제곱법의 분류는 다음과 같다.
1. Linear Least Squares : 선형
- Ordinary Least Squares
- Weighted Least Squares : 등분산성이 보장되지 않을 때
- Generalized Lieast Squares : 등분산성뿐만 아니라 자기상관 등 문제가 있을
2. Non-Linear Least Squares
보통최소제곱법 (Ordinary Least Squares, OLS)의 계산법
지금부터는 실제로 잔차 제곱의 합을 최소화하는 기울기와 $y$절편을 구해보고자 한다.
직선의 방정식은 다음과 같다고 하자
$$y=ax+b$$
데이터는 $n$개의 표본으로 이루어져 있으며, 각 데이터는 다음과 같이 표현된다
$$X_{i} (x_i, y_i), where \; i\in\mathbb{N}\; AND\; 1\leq i\leq n $$
그럼 $X_{i} (x_i, y_i)$의 잔차 $d_i$는 다음과 같이 계산된다.
$$d_i=y_i - (ax_i +b) $$
잔차의 제곱의 합은 다음과 같다.
$$\sum_{i=1}^{n} {\left(y_i -ax_i-b \right)^2}$$
이 값이 최소화되는 지점에서는 $a$에 대해서든, $b$에 대해서든 편미분을 하면 0이 된다.
$$ \frac {\partial} {\partial a} \sum_{i=1}^{n} {\left(y_i -ax_i-b \right)^2} =-2\sum_{i=1}^{n} {x_i \left(y_i - ax_i -b \right) } = 0 \cdots (1) $$
$$ \frac {\partial} {\partial b} \sum_{i=1}^{n} {\left(y_i -ax_i-b \right)^2} =-2\sum_{i=1}^{n} {\left(y_i - ax_i -b \right)}=0 \cdots (2) $$
(2)식에서 다음을 얻는다.
$$ \begin{align} b&= \frac {\sum_{i=1}^{n} y_i} {n} - a \frac {\sum_{i=1}^{n} x_i}{n} \\ &=\bar{Y} - a\bar{X} \\&&\end{align} $$
이를 (1) 식에 대입하면 다음을 얻는다.
$$ \begin{align} a &= \frac {\sum_{i=1}^{n}x_i \left( y_i - \frac {\sum_{i=1}^{n} y_i } {n} \right)} {\sum_{i=1}^{n} x_i \left(x_i - \frac {\sum_{i=1}^{n} x_i} {n} \right)} \\ &= \frac {\sum_{i=1}^{n} x_i \left( y_i - \bar{Y} \right)} {\sum_{i=1}^{n} x_i \left( x_i - \bar{X} \right)} \cdots(3) \\&&\end{align}$$
한편,
$$ \sum_{i=1}^{n} \left( \bar{X}^2 - x_i \bar{X} \right)= \bar{X} \sum_{i=1}^{n} \left( \bar{X} - x_i \right)=0$$
$$ \sum_{i=1}^{n} \left( \bar{X}y_i - \bar{X}\bar{Y} \right)=\bar{X} \sum_{i=1}^{n} \left( y_i - \bar{Y} \right)=0$$
이므로 (3)식의 분자, 분모는 다음과 같이 쓸 수 있다.
$$\sum_{i=1}^{n} x_i \left(y_i - \bar{Y} \right) = \sum_{i=1}^{n} \left[ x_i \left(y_i - \bar{Y}\right)- \left(\bar{X} y_i - \bar{X}\bar{Y} \right)\right] = \sum_{i=1}^{n} \left(x_i - \bar{X} \right) \left( y_i - \bar{Y} \right) = (n-1) cov \left(X,Y \right) $$
$$\sum_{i=1}^{n} x_i \left( x_i - \bar{X} \right)=\sum_{i=1}^{n} \left[ x_i \left( x_i - \bar{X} \right) + \left( -x_i\bar{X} + \bar{X}^2 \right) \right]=\sum_{i=1}^{n} \left( x_i - \bar{X} \right)^2 =(n-1) var(X)$$
따라서 다음을 얻는다.
$$a= \frac {cov \left(X,Y \right)} {var(X)}$$
$$b=\bar{Y} - \bar{X} \frac {cov \left(X,Y \right)} {var(X)}$$
값이 하나라는 점에서도 알 수 있지만, Local minima가 존재하지 않음을 알 수 있고, 이는 바로 global minima임을 알 수 있다.
이렇게, 선형 회귀분석에서 적절한 회귀 계수들을 찾는 방법인 최소제곱법에 대해 알아보았다. '최소제곱법을 통해 구한 값이 정말 최적일까?'라는 질문에 대한 답변은 '가우스-마르코프 정리 Gauss-Markov Theorem'을 통해 얻을 수 있다. 해당 내용은 다음 링크에서 알아볼 수 있다. 링크 추가 예정
[이론] 보통최소제곱법 (Ordinary Least Squares) 정복 완료!
작성일: 2023.06.15.
최종 수정일: 2023.06.15.
'통계 이론' 카테고리의 다른 글
| [이론] 가우스-마르코프 정리 (Gauss-Markov Theorem) (0) | 2023.06.21 |
|---|---|
| [이론] 로지스틱 회귀분석에서 회귀 계수를 구하는 방법 - Maximum likelihood estimation (0) | 2022.11.25 |
| [이론] 콕스 회귀 모델에서 생존 함수의 표현 (0) | 2022.11.10 |
| [이론] 생존 함수와 위험 함수의 관계 (0) | 2022.11.10 |
| [이론] p-value에 관한 고찰 (0) | 2022.09.05 |