
[이론] 카이 제곱 검정과 피셔 정확 검정의 관계
범주형 자료 분석을 할 때 "기대 빈도가 5 미만인 셀이 25% 이상인 경우 카이 제곱 검정을 신뢰할 수 없으며 피셔 정확 검정의 결과를 확인해야 한다."라는 말을 정말 많이 보게 된다. 도대체 카이 제곱 검정과 피셔 정확 검정이 무슨 관계이길래 이렇다는 건지 궁금증이 유발될 것이다. 모든 것을 설명할 수는 없지만, 왜 이런 이야기들이 나오는지 대략적으로 설명하고자 한다.
본 글을 읽기 전에 카이 제곱 검정과 피셔 정확 검정의 이론 내용에 관한 포스트를 읽고 오기를 강력히 권한다.
카이 제곱 검정: 2022.08.16 - [통계 이론] - [이론] 카이 제곱 검정 (Chi-squared test)
피셔 정확 검정: 2022.08.26 - [통계 이론] - [이론] 피셔 정확 검정 (Fisher's exact test)
카이 제곱 검정=근사, 피셔 정확 검정=정확
먼저 이해해야 하는 것은 "왜 카이 제곱 검정을 쓰게 되었는가?"일 것이다. 결론적으로는 정확한 방법인 피셔 정확 검정 시 계산량이 너무 방대하여 그에 근사하는 카이 제곱 분포를 사용했다는 것이다.
물론 Pearson 경이 어떤 생각으로 카이 제곱 검정을 만들었는지 정확하게 알 수는 없을 뿐 아니라, 그나마 세간에 알려진 이유도 나에게는 그다지 와닿지는 않는다. 피어슨 경의 생각을 읽어보면 아마도 다음과 같을 것이다. (따라서 본 포스팅은 문헌을 리뷰하거나 참고한 것이 아니며 피어슨 입장에서 생각해본 '뇌피셜'이다.)
분포가 무엇인지 대충이라도 상상해보기
흡연과 폐암의 빈도 표가 다음과 같다고 하자.
| 흡연자 | 비흡연자 | 총합 | |
| 폐암 환자 | (A) | 200 | |
| 정상인 | 800 | ||
| 총합 | 300 | 700 | 1000 |
각 셀 안의 값은 정확히 모르지만 빨간색으로 표시된 총합의 값은 정확히 알려져 있다고 하자. 이때 (A)에 들어갈 수 있는 숫자는 이론적으로 0부터 200 사이의 값이다. 흡연과 폐암에 아무런 관련성이 없을 때 (A)에 들어갈 것으로 생각되는 숫자를 생각해보자. 폐암은 흡연과 관련이 없고, 전체 인구 중 흡연자는 30%를 차지하므로 폐암 환자 200명 중 30%인 60명이 있을 것으로 기대된다. 당연하게도 60명이 있을 확률이 가장 높아야 하고, 60보다 커지거나 작아질수록 그 확률은 감소해야 한다. 따라서 확률 분포 함수는 다음과 같을 것이다.
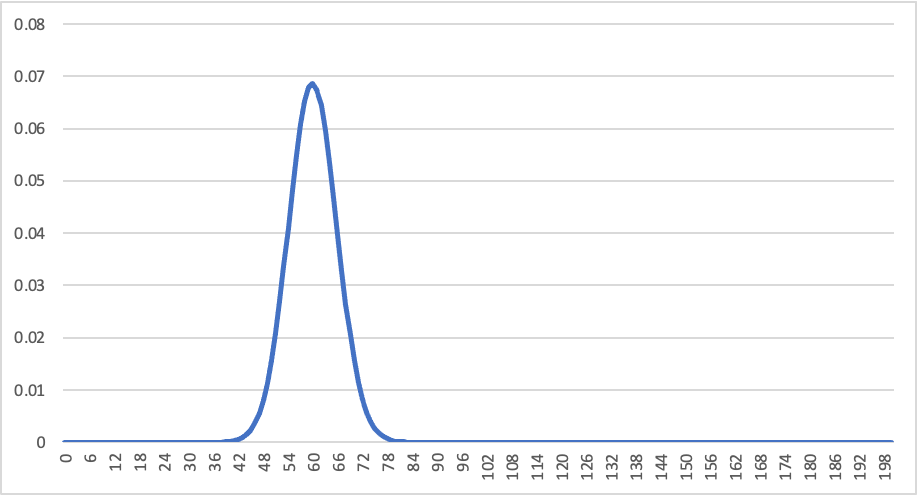
대립 가설 검정하기 <흡연자일수록 폐암환자일 가능성이 높아지는 관련성이 있다.> (One-sided, One-Tailed)
실제로 관찰 빈도가 다음과 같았다고 하자.
| 관찰 빈도 | 흡연자 | 비흡연자 | 총합 |
| 폐암 환자 | 75 | 125 | 200 |
| 정상인 | 225 | 575 | 800 |
| 총합 | 300 | 700 | 1000 |
아무런 관련성이 없었다면 폐암 환자이면서 흡연자일 것으로 예상되는 사람의 수는 60명이었는데 75명이 관찰되었으므로 흡연자일수록 폐암환자일 가능성이 높아질 것이라고 예상해볼 수 있다. 이것이 통계적으로 유의미한지 확인하는 사고 과정은 다음과 같다.
"흡연자이면서 폐암환자로 예상된 사람은 60명이었는데 75명이나 있네?"
$\rightarrow$ "이 말은 폐암과 흡연이 관련성이 있다는 것 아닐까?"
$\rightarrow$ [가정] "흡연이랑 폐암 간에 아무런 관계가 없다고 가정해보자."
$\rightarrow$ "그런 가정 하에서 흡연자이면서 폐암환자인 사람이 75명 이상일 확률이 얼마인지 구해보자."
계산 방법: 아래 수식을 모두 합한다.
$$75명일 확률 = \frac{\begin{pmatrix} 300 \\ 75 \end{pmatrix} \times \begin{pmatrix} 700 \\ 125 \end{pmatrix}} {\begin{pmatrix} 1000 \\ 200 \end{pmatrix}}$$
$$76명일 확률 = \frac{\begin{pmatrix} 300 \\ 76 \end{pmatrix} \times \begin{pmatrix} 700 \\ 124 \end{pmatrix}} {\begin{pmatrix} 1000 \\ 200 \end{pmatrix}}$$
$$77명일 확률 = \frac{\begin{pmatrix} 300 \\ 77 \end{pmatrix} \times \begin{pmatrix} 700 \\ 123 \end{pmatrix}} {\begin{pmatrix} 1000 \\ 200 \end{pmatrix}}$$
$$\vdots$$
$$200명일 확률 = \frac{\begin{pmatrix} 300 \\ 200 \end{pmatrix} \times \begin{pmatrix} 700 \\ 0 \end{pmatrix}} {\begin{pmatrix} 1000 \\ 200 \end{pmatrix}}$$
위 값들을 모두 더하면 0.00674213이다.
$\rightarrow$ "이 정도의 확률은 현실적에서 일어나기는 어려운 일 아니야?"
$\rightarrow$ "그러면 차라리 흡연자일수록 폐암에 걸릴 확률이 높은 게 진실이고 그런 현실 속에서 발생한 일이라고 보는 게 낫겠다."
위 사고 구조의 비현실성: 방대한 계산량
위 사고 과정은 틀린 것이 없고 논리적이기만 하다. 하지만 피어슨(Pearson) 경이 활동했을 1900년 경에는 복잡한 계산을 순식간에 해줄 계산기가 없었기 때문에, "75명일 확률", "76명일 확률", "77명일 확률",... , "200명일 확률"을 일일이 계산한다는 것은 굉장히 귀찮고 시간이 많이 걸리지만 그에 비해 그만한 가치는 별로 없는 일이었을 것이다.
예를 들어 "75명일 확률"만 하더라도
$$75명일 확률 = \frac{\begin{pmatrix} 300 \\ 75 \end{pmatrix} \times \begin{pmatrix} 700 \\ 125 \end{pmatrix}} {\begin{pmatrix} 1000 \\ 200 \end{pmatrix}}= \frac {\frac {300!} {75! \times 225!}\times \frac {700!} {125! \times 575!}} { \frac {1000!} {200! \times 800!}} $$
와 같은데, 저 계산을 한다는 것은 아주 매우 많이 귀찮은 일일 것이다.
근사하는 분포를 만들자
그래서 피어슨 경은 초기하 분포 (hypergeometric distribution)를 계산이 이미 되어있는 어떤 분포에 근사 시키고자 하는 욕구가 들었을 것이다. 아마도 피어슨 경은 두 번의 근사를 통해 초기하 분포를 정규분포에 근사 시키고자 했을 것이다.
1) 초기하 분포 (hypergeometric distribution)에서 이항 분포(binomial distribution)로
2) 이항 분포 (binomial distribution)에서 정규 분포 (normal distribution)로
1) 초기하 분포 (hypergeometric distribution)에서 이항 분포(binomial distribution)로
| 흡연자 | 비흡연자 | 총합 | |
| 폐암 환자 | $k$ | $n-k$ | $n$ |
| 정상인 | |||
| 총합 | $K$ | $N-K$ | $N$ |
위와 같은 상황에서 다음 조건을 만족하면 초기하 분포는 이항 분포로 근사 시킬 수 있다.
$$K>0.1 \times N$$
2) 이항 분포 (binomial distribution)에서 정규 분포 (normal distribution)로
어떤 이항 분포의 시행 횟수가 $n$, 발생 확률이 $p$일 때, $np>5, n(1-p)>5$이면 이항 분포는 정규 분포로 근사될 수 있다.
여기에서 $np$와 $n(1-p)$는 각각 사건이 일어나 기댓값과 일어나지 않을 기댓값을 의미한다. "기대 빈도가 5 미만인 셀이 25% 이상인 경우 카이 제곱 검정을 신뢰할 수 없으며 피셔 정확 검정의 결과를 확인해야 한다."라는 말은 여기에서 기인한 것으로 보인다.
근사하는 정규분포를 지정하자
정규 분포의 확률 밀도 함수 (probability density function)은 다음과 같다.
$$ {\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}$$
갑자기 수식 이야기를 왜 하느냐?
수식을 보면 정규 분포를 정의하는 데에 오직 평균($\mu$)과 표준편차($\sigma$)만이 필요하다는 것을 알 수 있다. 즉, 초기하 분포의 평균과 표준편차 (혹은 분산)를 알아내면 근사하는 정규분포를 지정할 수 있다.
(1) 평균
초기하 분포 (hypergeometric distribution)의 이산 밀도 함수 (discrete density function)은 $$f_{k} (k;K,N,n)= \frac{\begin{pmatrix} K \\ k \end{pmatrix} \times \begin{pmatrix} N-K \\ n-k \end{pmatrix}} {\begin{pmatrix} N \\ n \end{pmatrix}}$$ 이므로 평균($\mu$)은 다음과 같이 구할 수 있다.
$$\begin{align} \mu &=\sum _{k} {k \times \frac{\begin{pmatrix} K \\ k \end{pmatrix} \times \begin{pmatrix} N-K \\ n-k \end{pmatrix}} {\begin{pmatrix} N \\ n \end{pmatrix}} } \\&=\sum _{k} {K \times \frac{\begin{pmatrix} K-1 \\ k-1 \end{pmatrix} \times \begin{pmatrix} N-K \\ n-k \end{pmatrix}} {\begin{pmatrix} N \\ n \end{pmatrix}} } \\&=\sum _{k} {K \times \frac{\begin{pmatrix} K-1 \\ k-1 \end{pmatrix} \times \begin{pmatrix} N-K \\ n-k \end{pmatrix}} {\frac{N}{n} \times \begin{pmatrix} N-1 \\ n-1 \end{pmatrix}} } \\&= \frac {Kn} {N} \\&&\end{align} $$
(2) 분산
분산은 다음과 같이 계산할 수 있다.
$$ \begin{align} \sigma^{2}&=\sum _{k} {k^{2} \times \frac{\begin{pmatrix} K \\ k \end{pmatrix} \times \begin{pmatrix} N-K \\ n-k \end{pmatrix}} {\begin{pmatrix} N \\ n \end{pmatrix}} } - \mu^{2} \\ &=\sum _{k} {Kk\times \frac{\begin{pmatrix} K-1 \\ k-1 \end{pmatrix} \times \begin{pmatrix} N-K \\ n-k \end{pmatrix}} {\begin{pmatrix} N \\ n \end{pmatrix}} } - \left( \frac {Kn} {N} \right)^{2} \\& =K \left( \sum _{k} { \left(k-1\right)\times \frac{\begin{pmatrix} K-1 \\ k-1 \end{pmatrix} \times \begin{pmatrix} N-K \\ n-k \end{pmatrix}} {\begin{pmatrix} N \\ n \end{pmatrix}} } + \sum _{k} { \times \frac{\begin{pmatrix} K-1 \\ k-1 \end{pmatrix} \times \begin{pmatrix} N-K \\ n-k \end{pmatrix}} {\begin{pmatrix} N \\ n \end{pmatrix}} } \right) - \left( \frac {Kn} {N} \right)^{2} \\&=K \left( \sum _{k} { \left(K-1\right)\times \frac{\begin{pmatrix} K-2 \\ k-2 \end{pmatrix} \times \begin{pmatrix} N-K \\ n-k \end{pmatrix}} { \frac{N \left( N-1 \right)}{ n \left( n-1\right)} \begin{pmatrix} N-2 \\ n-2 \end{pmatrix}} } + \sum _{k} { \times \frac{\begin{pmatrix} K-1 \\ k-1 \end{pmatrix} \times \begin{pmatrix} N-K \\ n-k \end{pmatrix}} {\frac{N} {n} \begin{pmatrix} N-1 \\ n-1 \end{pmatrix}} } \right) - \left( \frac {Kn} {N} \right)^{2}\\&=\frac {K(K-1)n(n-1)} {N(N-1)} + \frac {Kn} {N} - \left( \frac {Kn} {N} \right)^{2}\\&= n \cdot \frac {K} {N} \frac {N-K} {N} \frac {N-n} {N-1} \\&& \end{align} $$
다른 방법으로는 factorial moment를 사용하여 $[E(X(X-1))]$을 구하는 방법도 있다. 수식이 조금 더 간단해진다.
따라서 흡연자이면서 폐암 환자인 사람의 수는 평균이 $\frac {Kn} {N} $, 분산이 $n \cdot \frac {K} {N} \frac {N-K} {N} \frac {N-n} {N-1} $인 정규분포를 따른다고 할 수 있다.
정규 분포가 아닌 카이 제곱 분포를 사용하자
피어슨 경은 이 정규 분포를 바로 사용하는 것이 아니라 카이 제곱 분포를 사용하고자 했다. 이런 2*2 분할표 (contingency table)에서는 정규 분포를 쓰든 카이 제곱 분포를 쓰든 아무 상관이 없겠지만 표가 더 커지면 문제가 발생하기 마련이다.
<2*2 분할표>
| 범주1(1) | 범주1(2) | 합계 | |
| 범주2(1) | (A) | ||
| 범주2(2) | |||
| 합계 |
<3*3 분할표>
| 범주1(1) | 범주1(2) | 범주1(3) | 합계 | |
| 범주2(1) | (ㄱ) | (ㄴ) | ||
| 범주2(2) | (ㄷ) | (ㄹ) | ||
| 범주2(3) | ||||
| 합계 |
2*2 분할표에서는 자유도가 1이므로 한 개의 값만 지정하면 되지만, 3*3 분할표만 되어도 자유도가 4이므로 자유롭게 정할 수 있는 값이 4개가 된다. 이런 경우 정규 분포를 바로 사용할 수 없다. 따라서 정규분포를 사용하지만 자유도의 개념이 있는 카이 제곱 분포를 사용하고자 했을 것이다.
설명을 용이하게 하기 위해 2*2 분할표로 설명을 이어가도록 하겠다. 흡연자이면서 폐암 환자인 사람의 수($X$)를 표준화한 뒤 제곱해주면 카이 제곱 분포를 따른다고 할 수 있다. 평균이 $\frac {Kn} {N} $, 분산이 $n \cdot \frac {K} {N} \frac {N-K} {N} \frac {N-n} {N-1} $이므로
$$\frac{\left(X-\frac {Kn} {N}\right)^2}{ n \cdot \frac {K} {N} \frac {N-K} {N} \frac {N-n} {N-1} }\sim \chi^2(1) \tag{1}$$
이라고 작성할 수 있다.
이때 $N$이 굉장히 크면 $N\sim \left(N-1\right)$이므로 $(1)$식은 $$\frac{\left(X-\frac {Kn} {N}\right)^2}{ n \cdot \frac {K \cdot (N-K) \cdot(N-n)} {N^3}}\sim \chi^2(1) \tag{2}$$
에 근사 시킬 수 있다.
수식을 정리해보자
한편 수식$(2)$에서 쓰인 문자들은 표에서 다음과 같이 나타난다.
| 관찰 빈도 | 흡연자 | 비흡연자 | 총합 |
| 폐암 환자 | $a_{11}=X$ | $a_{12}=n-X$ | $n$ |
| 정상인 | $a_{21}=K-X$ | $a_{22}=N-K-n+X$ | $N-n$ |
| 총합 | $K$ | $N-K$ | $N$ |
수식$(2)$을 어떻게 잘 정리해야 세상에 잘 먹힐지 피어슨 경은 고민이 많았을 것이다. 저 식은 너무 복잡해서 일반적인 연구자가 쓰기엔 복잡할 뿐만 아니라 쓰고 싶지 않게 생겼기 때문이다. 피어슨 경은 뛰어난 직관으로 해결했을 수도 있지만 나에게는 다음과 같이 계산되는 결과가 매력적으로 느껴졌다.
먼저 기대 빈도를 구하면 다음과 같다.
| 기대 빈도 | 흡연자 | 비흡연자 | 총합 |
| 폐암 환자 | $$e_{11}=\frac {Kn} {N}$$ | $$e_{12}=\frac {(N-K)n} {N}$$ | $n$ |
| 정상인 | $$e_{21}=\frac {K(N-n)} {N}$$ | $$e_{22}=\frac {(N-K)(N-n)} {N}$$ | $N-n$ |
| 총합 | $K$ | $N-K$ | $N$ |
관찰 빈도에서 기대 빈도를 뺀 뒤 제곱한 값은 놀랍게도 모든 셀에서 같다. (사실 자유도가 1이므로 당연한 현상이긴 하다.)
| $$\left(관찰 빈도-기대 빈도\right)^2 $$ | 흡연자 | 비흡연자 |
| 폐암 환자 | $$\left(a_{11}-e_{11}\right)^2=\left( X- \frac{Kn}{N} \right)^2$$ | $$\left(a_{12}-e_{12}\right)^2=\left( X- \frac{Kn}{N} \right)^2$$ |
| 정상인 | $$\left(a_{21}-e_{21}\right)^2=\left( X- \frac{Kn}{N} \right)^2$$ | $$\left(a_{22}-e_{22}\right)^2=\left( X- \frac{Kn}{N} \right)^2$$ |
게다가 이 값은 수식$(2)$인 $\frac{\left(X-\frac {Kn} {N}\right)^2}{ n \cdot \frac {K \cdot (N-K) \cdot(N-n)} {N^3}}$의 분자에 해당하는 내용이다. 따라서 이 수식은 다음과 같이 바꿔보고 싶은 욕구가 차오른다.
$$ \begin{align} \frac{\left(X-\frac {Kn} {N}\right)^2}{ n \cdot \frac {K \cdot (N-K) \cdot(N-n)} {N^3}}&=\frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{Kn}{N}} \frac{\frac{Kn}{N}}{ n \cdot \frac {K \cdot (N-K) \cdot(N-n)} {N^3}}\\&= \frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{Kn}{N}} \left( 1+ \frac{N^2}{(N-K)(N-n)}-1\right)\\&= \frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{Kn}{N}} + \frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{Kn}{N}} \frac{KN+Nn-Kn}{(N-K)(N-n)}\\&=\frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{Kn}{N}} + \frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{K(N-n)}{N}} \frac{KN+Nn-Kn}{(N-K)n}\\&=\frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{Kn}{N}} + \frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{K(N-n)}{N}} \left( 1 + \frac{KN} {(N-K)n} \right)\\&=\frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{Kn}{N}} + \frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{K(N-n)}{N}} +\frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{K(N-n)}{N}} \frac{KN} {(N-K)n} \\&=\frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{Kn}{N}} + \frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{K(N-n)}{N}} +\frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{(N-K)n}{N}} \frac{N} {(N-n)} \\&= \frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{Kn}{N}} + \frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{K(N-n)}{N}} +\frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{(N-K)n}{N}} \left( 1+ \frac{n} {(N-n)} \right)\\&=\frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{Kn}{N}} + \frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{K(N-n)}{N}} +\frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{(N-K)n}{N}} + \frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{(N-K)(N-n)}{N}} \\&= \frac {\left(a_{11}-e_{11}\right)^2} {e_{11}} +\frac {\left(a_{21}-e_{21}\right)^2} {e_{21}} +\frac {\left(a_{12}-e_{12}\right)^2} {e_{12}}+\frac {\left(a_{22}-e_{22}\right)^2} {e_{22}} \\&= \sum_{i, j} \frac {\left(a_{ij}-e_{ij}\right)^2} {e_{ij}} \tag{3} \\&& \end{align}$$
정리된 수식의 위엄
이제 정확한 초기하 분포의 확률을 구하기 위해 $1000!$같은 무식한 계산을 하지 않아도 된다. $2*2$ 분할표라면 관찰 빈도와 기대 빈도로 계산한 $(3)$ 식의 값이 3.84를 넘기만 하다면 분포에 통계적으로 유의한 차이가 있다고 양측 검정 (Two-tailed or two-sided)을 한 셈이니 말이다. (3.84는 자유도가 1인 카이 제곱 분포의 누적 확률이 0.95가 되는 지점이다.) $m*n$ 분할표일 때에도 식 $(3)$과 비슷하게 계산을 먼저 하고 그 값이 카이 제곱 분포표에서 자유도 $(m-1)\times(n-1)$일 때 $\alpha=0.05$인 지점보다 큰지만 확인하면 된다.
[이론] 카이 제곱 검정과 피셔 정확 검정의 관계 정복 완료!
작성일: 2022.08.29.
최종 수정일: 2022.08.29.
'통계 이론' 카테고리의 다른 글
| [이론] p-value에 관한 고찰 (0) | 2022.09.05 |
|---|---|
| [이론] 연속성을 수정한 카이 제곱 검정 (Chi-squared test with Yates's correction for continuity) (0) | 2022.08.30 |
| [이론] 피셔 정확 검정 (Fisher's exact test) (0) | 2022.08.26 |
| [이론] 카이 제곱 검정 (Chi-squared test) (3) | 2022.08.16 |
| [이론] Q-Q Plot (Quantile-Quantile Plot) (0) | 2022.08.12 |