
[이론] Q-Q Plot (Quantile-Quantile Plot)
정규성을 검정할 때 Q-Q Plot을 쓰곤 한다. 그런데 이런 궁금증이 들 수 있다.
왜 Q-Q Plot이 직선에 가까운 것이 정규성을 따른다는 뜻인가?
이에 대해 조목조목 설명해나갈 것이다.
먼저, 정규성을 따른다는 것이 어떤 의미인지 명확히 이해하고, 명확하게 설명할 수 있어야 한다.
정규성을 따른다는 것이 무엇인가?
정규성을 따른다는 것을 가장 쉽게 말하자면, 이는 히스토그램이 정규분포 곡선과 같이 종모양으로 생겼다는 것을 의미한다.
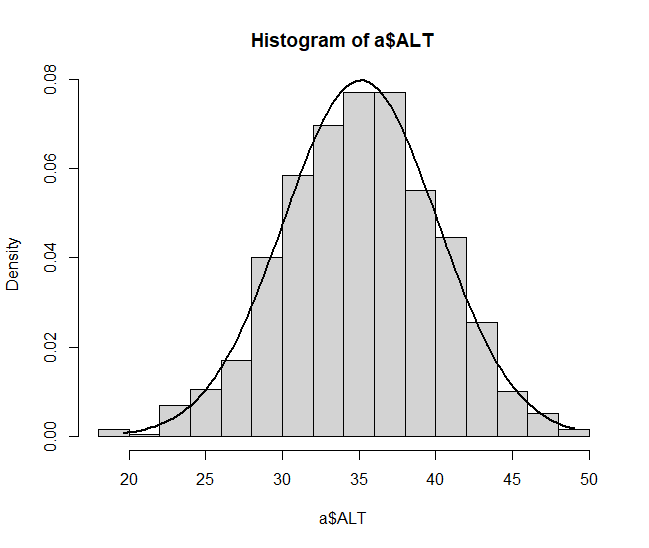
그렇다면 정규분포 곡선은 무엇을 의미하는가?
[사전 지식: 확률 밀도 함수의 그래프 아래 전체 면적은 1이다.]
어렵게 표현하자면 정규분포곡선은 정규분포의 확률 밀도 함수 (Probability Density Function, PDF)다. 그리고 확률 밀도 함수의 적분 값은 대상의 분율을 의미한다. 이해할 수 있는 언어로 표현하면 다음과 같다. 현실 세계에서 ALT의 분포는 정규분포를 따른다고 가정하자. 이때 아래 그림은 ALT의 분포를 나타낸 것이다. 여기에서 파란색으로 칠한 부분의 면적은 0.84인데 이 말은 전체 인구 중 84%의 ALT가 40 이하라는 뜻이다. 즉 전체 인구가 100명이라면 ALT 작은 순서대로 줄을 세웠을 때 84번째 서있는 사람의 ALT는 40이 된다.
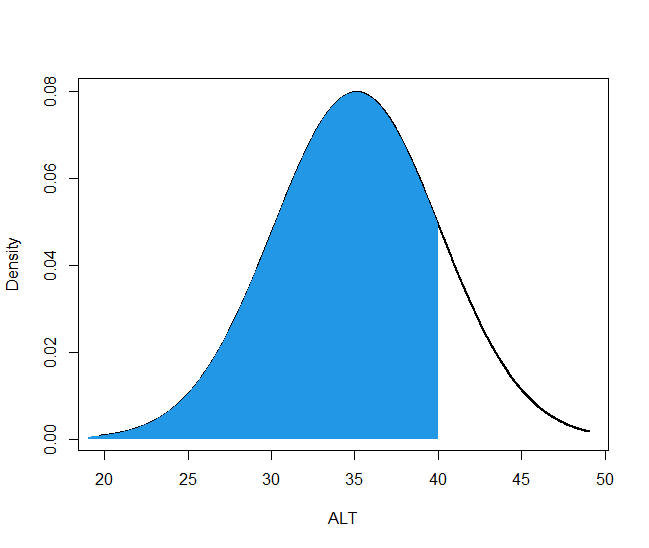
우리가 연구를 할 때 인구 전체를 대상으로 할 수는 없고 일부를 표본으로 뽑을 수밖에 없다. 설명을 용이하게 하기 위해 간단한 상황으로 전체 인구 중 3명을 뽑는 상황을 가정해보자. 누군가 ALT가 높거나 낮은 사람이 잘 뽑히도록 조작을 하지 않는 한 평균 정도에 있는 사람이 한 명, 평균 이하인 사람 중 한 명, 평균 이상인 사람 중 한 명이 뽑힐 것이라고 생각하는 것이 상식적이다.
위 그래프는 평균을 기준으로 대칭이므로 종 모양의 가장 높은 곳에 평균이 위치한다. 또한, 확률 밀도 함수 곡선 아래 면적은 1과 같으므로 아래 보라색 영역의 면적은 0.5와 같다. (평균은 35.1이다.)
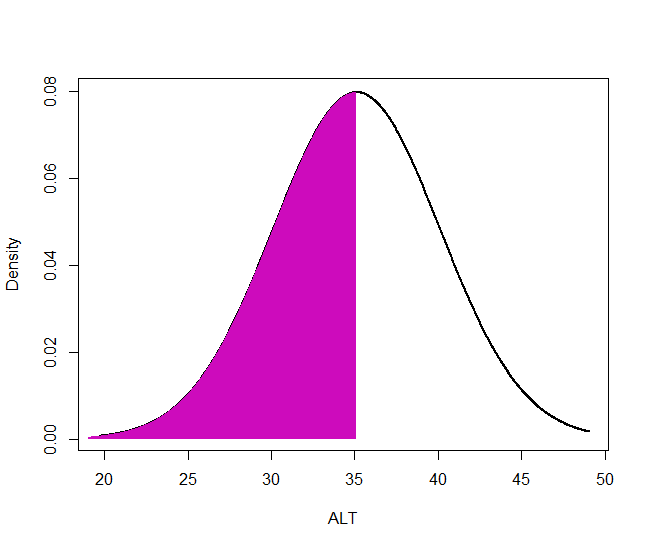
평균 이하인 사람 중 한 명은 어디에서 고르는 것이 합리적일까? 당연히 중간이다. 그런데 중간이 어디인지 어떻게 아는가? ALT의 최솟값이 19, 평균이 35이므로 두 값의 정중앙인 27로 골라야 하는가? 아니다. 평균 이하인 사람이 50명이라면 순서대로 줄을 세운 뒤 정중앙인 25번째에 서있는 사람을 골라야 한다. 줄을 세운 뒤 몇 등인지 확인하는 것은 정규분포 곡선 아래 면적을 구하는 것과 같으므로 왼쪽 끝에서부터 적분했을 때 0.25가 되는 ALT값을 찾아야 한다. 즉, 아래 그림에서 초록색 면적이 0.25가 되는 ALT값을 찾아야 한다. (이 ALT 값은 31.7이다)
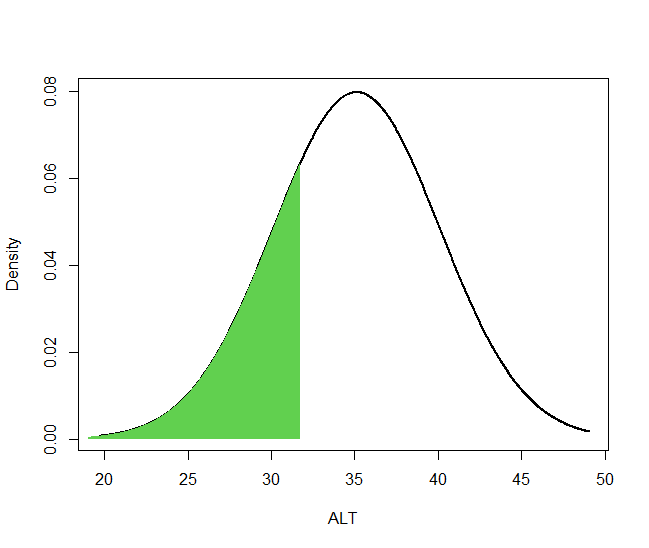
평균 이상인 사람 중 한 명을 고르는 것도 같은 논리가 적용된다. 곡선 아래 면적이 0.75인 ALT값을 찾아야 한다. 즉, 아래 그림에서 노란색 면적이 0.75가 되는 ALT값을 찾아야 한다. (이 ALT 값은 38.5이다)
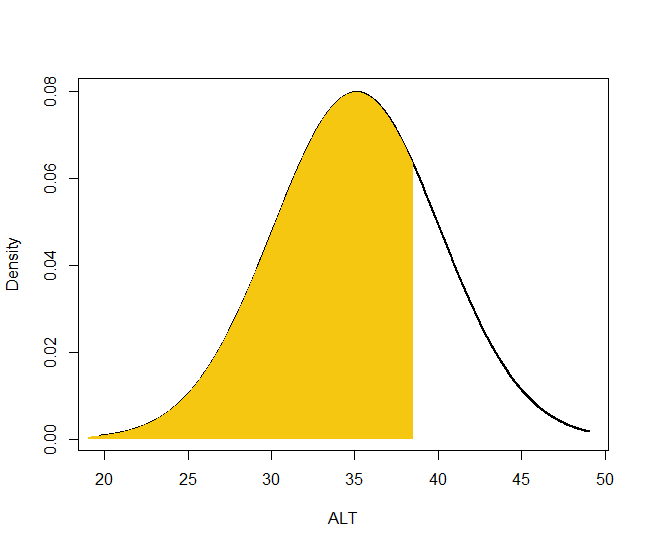
따라서 전체 인구 중 3명을 뽑았는데 그 ALT값이 각각 31.7, 35.1, 38.5였다면 정규분포를 따른다고 생각할 수 있다. (물론 이 예시는 3명이므로 당연히 정규분포를 따른다고 결론 내리는 것이 매우 부적절하다. 하지만 n수가 많다면 타당한 논리일 수 있다.)
거꾸로 생각해보기
그렇다면 위의 사전 지식이 없을 때 3명의 ALT 값이 각각 31.7, 35.1, 38.5였다면 이 값들이 정규분포를 따르는지 어떻게 확인할 수 있을까? 위의 과정을 그대로 거꾸로 쫓아가면 된다.
1) 데이터 줄세우고 상대적 위치 확인하기
ALT 값을 작은 순서대로 줄 세우면 31.7, 35.1, 38.5와 같다. 가장 작은 ALT값의 위치를 0, 가장 큰 ALT값의 위치를 1이라고 가정하면 중간의 35.1은 0.5에 위치한다고 볼 수 있고, 작은 값인 31.7은 0.25에 위치한다고 볼 수 있고, 큰 값인 38.5는 0.75에 위치한다고 볼 수 있다. 즉, 전체 인구가 100명이고 ALT가 정규분포를 따른다고 가정했을 때, 만약 25등의 ALT값이 31.7, 50등의 ALT값이 35.1, 75등의 ALT값이 38.5라면 3명의 데이터는 정규분포를 따른다고 생각할 수 있다.
2) 25등, 50등, 75등의 ALT값 확인하기
ALT의 평균은 35.1, 표준편차는 5.0이다. 그렇다면 평균이 35.1, 표준편차가 5.0인 정규분포 곡선을 그리고 왼쪽 끝에서부터 적분했을 때, 넓이가 0.25, 0.5, 0.75가 되는 ALT 값을 찾으면 된다. 그 값은 31.7, 35.1, 38.5이다. 이 위치는 정규분포를 따른다면 이론적으로 3명의 데이터가 위치해야 하는 곳을 의미한다.
3) [표본 3명의 ALT값]과 위에서 구한 [25등, 50등, 75등의 ALT값]을 비교하기
표본 3명의 ALT값은 31.7, 35.1, 38.5이고, 25등, 50등, 75등의 ALT값 이론적으로 31.7, 35.1, 38.5에 위치해야 한다. 실제 표본의 ALT값과 이론적인 값을 순서쌍으로 만들면 (31.7, 31.7), (35.1,35.1), (38.5, 38.5)다. 이를 좌표평면에 나타내면 일직선상에 존재하게 된다.
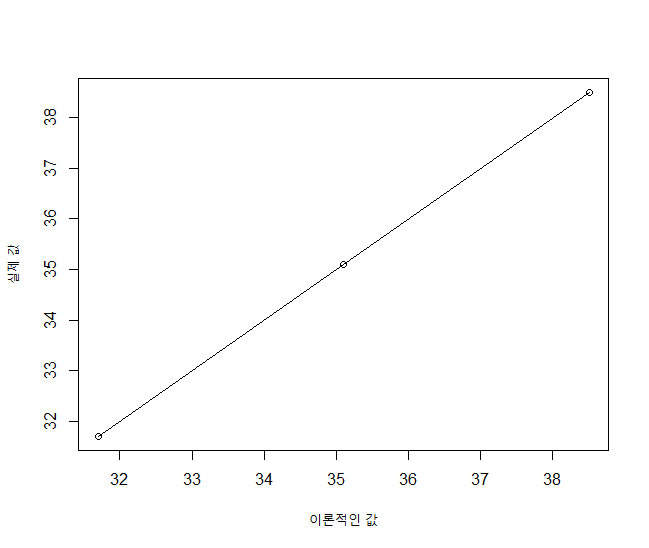
4) ALT의 평균과 표준편차를 모르는데?
일반적으로, 우리가 표본을 뽑아 연구하는 이유는 모집단 전체를 대상으로 연구하기엔 시간과 돈이 많이 소비되기 때문이다. 따라서 모집단의 ALT 평균과 표준편차를 알 리가 없다. 이미 알고 있다면 연구할 필요가 없다. 이럴 때 어떻게 할 수 있을까? 평균이 0, 표준편차가 1인 표준 정규분포를 이용하면 된다. 표준 정규분포 곡선을 왼쪽 끝에서부터 적분했을 때, 넓이가 0.25, 0.5, 0.75가 되는 Z값을 찾으면 된다. 그 값은 각각 -0.67, 0, 0.67이다.
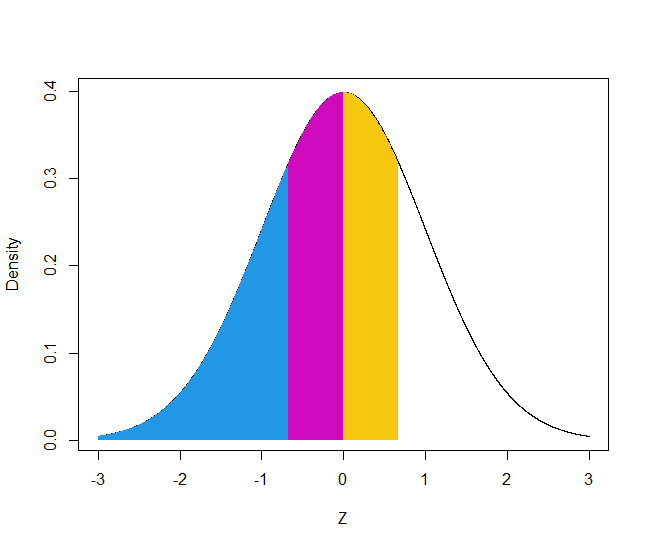
만약 모집단의 평균과 표준편차를 알고 있다면 다음 수식을 통해 이론적인 ALT 값(X)을 구할 수 있다.
$$Z=\frac{X-\mu}{\sigma}$$
하지만, 정규성을 따지는데 굳이 이론적인 값까지 알 필요는 없다. 정규성을 따른다면 실제 값과 이론적인 값(X)이 일직선상에 존재한다는 것은 이미 위에서 밝혔다. 그런데 위 수식에 의거 이론적인 값(X)은 Z와 선형 관계에 있다. 따라서 실제 값 또한 Z와 선형 관계에 있다. 따라서 정규성을 따른다면 실제 값은 Z와 선형 관계를 띄기 때문에 일직선 상에 위치하게 된다. 이 점에 착안하여 실제 값과 Z의 plot을 그린 것이 Q-Q plot이다.
또한 가로축에 Z, 세로축에 X를 놓는다면, 당연하게도 기울기는 $\sigma$가 된다.
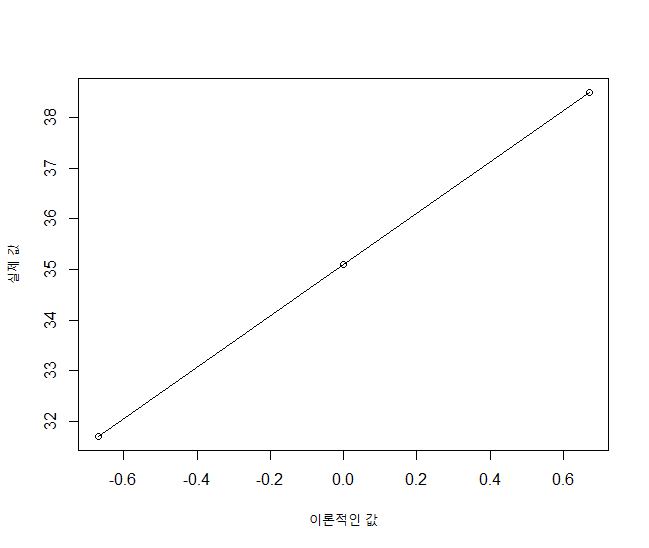
실제 Q-Q plot 그릴 때 다를 수 있는 점
여기까지 읽어본 독자 중 누군가는 Q-Q plot을 직접 그려보았을 수도 있다. (그리는 법은 다음 링크 참고:2022.08.11 - [기술 통계/R] - [R] 정규성 검정 (1) : QQplot - qqnorm(), qqline()) 그러면 위와 다른 그림을 그려주는 것을 확인할 수 있다.
코드
qq<-qqnorm(c(31.7, 35.1, 38.5))
identity(qq)결과
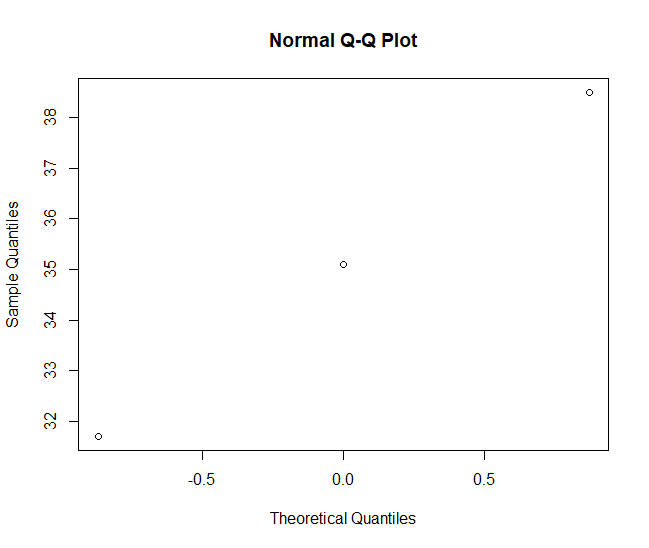
$x
[1] -0.8694238 0.0000000 0.8694238
$y
[1] 31.7 35.1 38.5
x축 위치가 (-0.67, 0, 0.67)이 아니다! 왜 이런 일이 발생한 것일까?
필자는 3명의 상대적 위치를 0.25, 0.5, 0.75로 잡았다. 하지만 상대적 위치를 어디로 잡는 것이 좋은가에 대해서는 갑론을박이 있을 수 있으며 많은 방법론이 다음 표와 같이 존재한다. 필자는 이해를 돕기 위해 가장 간단한 첫 번째 방법 (Van der Waerden)을 사용하였다.
| 방법 | 수식 |
| Van der Waerden | $$\frac{k}{n+1}$$ |
| Rankit | $$\frac{k-\frac{1}{2}}{n}$$ |
| Tukey | $$\frac{k-\frac{1}{3}}{n+\frac{1}{3}}$$ |
| Blom | $$\frac{k-\frac{3}{8}}{n+\frac{1}{4}}$$ |
R에서는 n수가 10 이하일 때까지는 Blom의 방법을, 11부터는 Rankit의 방법을 사용한다.
SPSS, R에서는 각각의 방법에 따라 Q-Q plot을 그릴 수 있다. 다음 링크에서 확인할 수 있다.
SPSS:
R:
[이론] Q-Q plot 정복 완료!
작성일: 2022.08.12.
최종 수정일: 2022.08.12.
이용 프로그램: R 4.1.3, RStudio v1.4.1717
운영체제: Windows 10
'통계 이론' 카테고리의 다른 글
| [이론] p-value에 관한 고찰 (0) | 2022.09.05 |
|---|---|
| [이론] 연속성을 수정한 카이 제곱 검정 (Chi-squared test with Yates's correction for continuity) (0) | 2022.08.30 |
| [이론] 카이 제곱 검정과 피셔 정확 검정의 관계 (0) | 2022.08.29 |
| [이론] 피셔 정확 검정 (Fisher's exact test) (0) | 2022.08.26 |
| [이론] 카이 제곱 검정 (Chi-squared test) (3) | 2022.08.16 |