의학 통계 코드 저장소

[R] 도수분포표 (Frequency table), 분할표 (Contingency table) 만들기 - CrossTable()

 이전 글에서 R로 도수분포표 및 분할표를 만드는 것이 얼마나 귀찮은 일인지 설명하였다. 이 글은 아래 글의 후속 글이므로 미리 읽고 오길 권한다.

2022.08.31 - [기술 통계/R] - [R] 도수분포표 (Frequency table), 분할표 (Contingency table) 만들기 - table(), prop.table(), xtabs(), margin.table()

이 귀찮은 일을 한꺼번에 해주는 함수로 CrossTable()이 있다. 이를 소개하고 한계점 및 일부 해결 방안을 소개한다.

*실습용 데이터는 아래 링크를 클릭하면 다운로드할 수 있습니다.

2022.08.04 - [공지사항 및 소개] - 분석용 데이터 (update 22.08.29)

코드를 보여드리기에 앞서 워킹 디렉토리부터 지정하겠다.

워킹 디렉토리에 관한 설명은 다음 링크된 포스트에서 볼 수 있다.

2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 라이브러리 만들기 - LIBNAME

setwd("C:/Users/user/Documents/Tistory_blog")

데이터를 불러와 df에 객체로 저장하겠다.

데이터 불러오는 방법은 다음 링크에서 볼 수 있다.

2022.08.05 - [통계 프로그램 사용 방법/R] - [R] 데이터 불러오기 : EXCEL - read_excel(), read.xlsx()

2022.08.10 - [통계 프로그램 사용 방법/R] - [R] 데이터 저장하기 : CSV 파일 - write.csv(), write_csv()

2022.08.10 - [통계 프로그램 사용 방법/R] - [R] 데이터 불러오기 : SAS file (.sas7bdat) - read.sas7bdat(), read_sas()

install.packages("readr")
library("readr")
df<-read_csv("Data.csv")

CrossTable() 함수는 gmodels라는 패키지에 있으므로 패키지를 설치한다.

패키지 설치 방법은 다음 글에서 볼 수 있다.

2022.08.05 - [통계 프로그램 사용 방법/R] - [R] 패키지 설치하기 - install.packages(), library()

install.packages("gmodels")
library("gmodels")

코드

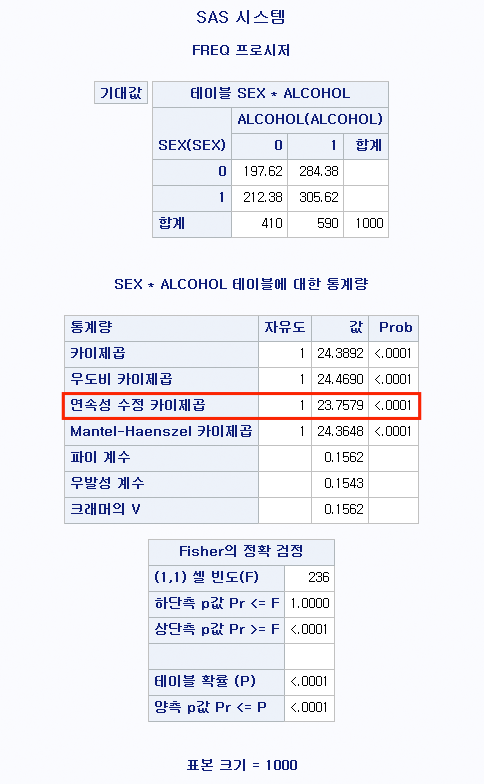
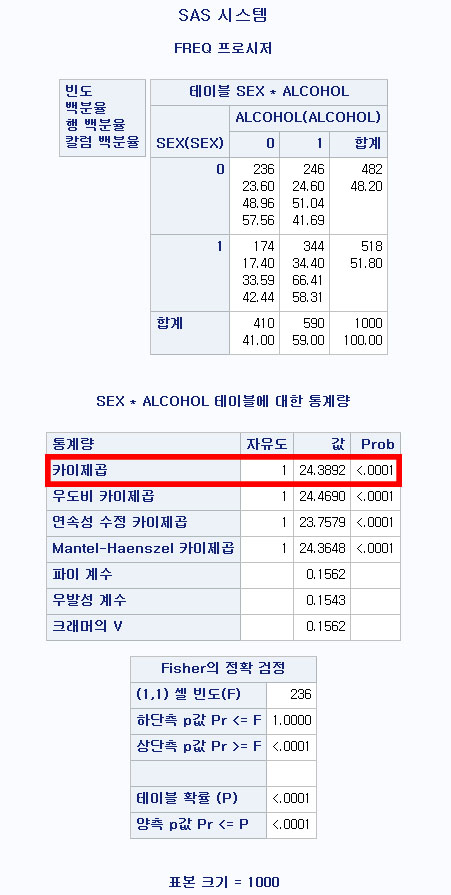
성별과 음주 여부에 대해 분할표를 작성하도록 하겠다.

CrossTable(df$SEX, df$ALCOHOL, prop.chisq=FALSE)

CrossTable(df$SEX, df$ALCOHOL, prop.chisq=FALSE) : 데이터 df에 있는 SEX와 ALCOHOL로 교차 표를 출력한다. 카이 제곱 검정 기여량은 출력하지 않는다. (백분율, 행백분율, 열백분율은 출력하는 것이 기본 설정이다.)

결과

   Cell Contents
|-------------------------|
|                       N |
|           N / Row Total |
|           N / Col Total |
|         N / Table Total |
|-------------------------|

 
Total Observations in Table:  1000 

 
             | df$ALCOHOL 
      df$SEX |         0 |         1 | Row Total | 
-------------|-----------|-----------|-----------|
           0 |       236 |       246 |       482 | 
             |     0.490 |     0.510 |     0.482 | 
             |     0.576 |     0.417 |           | 
             |     0.236 |     0.246 |           | 
-------------|-----------|-----------|-----------|
           1 |       174 |       344 |       518 | 
             |     0.336 |     0.664 |     0.518 | 
             |     0.424 |     0.583 |           | 
             |     0.174 |     0.344 |           | 
-------------|-----------|-----------|-----------|
Column Total |       410 |       590 |      1000 | 
             |     0.410 |     0.590 |           | 
-------------|-----------|-----------|-----------|

이전 글 (2022.08.31 - [기술 통계/R] - [R] 도수분포표 (Frequency table), 분할표 (Contingency table) 만들기 - table(), prop.table(), xtabs(), margin.table())과 거의 같은 결과가 도출된다.

코드-퍼센트를 산출 및 소수점 이하 숫자 제한하고 싶을 때

CrossTable(df$SEX, df$ALCOHOL, prop.chisq=FALSE, format=c("SPSS"), digits=2)

결과

  Cell Contents
|-------------------------|
|                   Count |
|             Row Percent |
|          Column Percent |
|           Total Percent |
|-------------------------|

Total Observations in Table:  1000 

             | df$ALCOHOL 
      df$SEX |        0  |        1  | Row Total | 
-------------|-----------|-----------|-----------|
           0 |      236  |      246  |      482  | 
             |    48.96% |    51.04% |    48.20% | 
             |    57.56% |    41.69% |           | 
             |    23.60% |    24.60% |           | 
-------------|-----------|-----------|-----------|
           1 |      174  |      344  |      518  | 
             |    33.59% |    66.41% |    51.80% | 
             |    42.44% |    58.31% |           | 
             |    17.40% |    34.40% |           | 
-------------|-----------|-----------|-----------|
Column Total |      410  |      590  |     1000  | 
             |    41.00% |    59.00% |           | 
-------------|-----------|-----------|-----------|

참 강력한 툴이지만 단점이 존재한다.

1) 도수분포표의 경우 누적 도수를 산출해주지 않는다.

2) 세 개 이상의 변수를 사용한 분할표를 작성해주지 않는다.

첫 번째 단점은 해결할 수 없다.

두 번째 단점인 "세 개 이상의 변수를 사용한 분할표"는 억지로 작성할 수는 있다. 

성별과 음주 여부에 관한 분할표를 고혈압 여부에 따라 작성하고자 한다고 하자. 그렇다면 고혈압이 있는 집단과 없는 집단을 미리 나눠놔야 한다.

코드

subsample_wohtn<-df[df$HTN==0,]
subsample_whtn<-df[df$HTN==1,]

CrossTable(subsample_wohtn$SEX, subsample_wohtn$ALCOHOL, prop.chisq=FALSE)
CrossTable(subsample_whtn$SEX, subsample_whtn$ALCOHOL, prop.chisq=FALSE)

subsample_wohtn<-df[df$HTN==0,] : 데이터 df의 HTN변수가 0인 사람만 뽑아 "subsample_wohtn"에 저장한다.
subsample_whtn<-df[df$HTN==1,] : 데이터 df의 HTN변수가 1인 사람만 뽑아 "subsample_whtn"에 저장한다.

CrossTable(subsample_wohtn$SEX, subsample_wohtn$ALCOHOL, prop.chisq=FALSE) : HTN변수가 0인 사람들로만 성별과 음주 여부의 분할표를 작성한다.
CrossTable(subsample_whtn$SEX, subsample_whtn$ALCOHOL, prop.chisq=FALSE) : HTN변수가 1인 사람들로만 성별과 음주 여부의 분할표를 작성한다.

결과

   Cell Contents
|-------------------------|
|                       N |
|           N / Row Total |
|           N / Col Total |
|         N / Table Total |
|-------------------------|

 
Total Observations in Table:  503 

 
                    | subsample_wohtn$ALCOHOL 
subsample_wohtn$SEX |         0 |         1 | Row Total | 
--------------------|-----------|-----------|-----------|
                  0 |       114 |       122 |       236 | 
                    |     0.483 |     0.517 |     0.469 | 
                    |     0.562 |     0.407 |           | 
                    |     0.227 |     0.243 |           | 
--------------------|-----------|-----------|-----------|
                  1 |        89 |       178 |       267 | 
                    |     0.333 |     0.667 |     0.531 | 
                    |     0.438 |     0.593 |           | 
                    |     0.177 |     0.354 |           | 
--------------------|-----------|-----------|-----------|
       Column Total |       203 |       300 |       503 | 
                    |     0.404 |     0.596 |           | 
--------------------|-----------|-----------|-----------|





   Cell Contents
|-------------------------|
|                       N |
|           N / Row Total |
|           N / Col Total |
|         N / Table Total |
|-------------------------|

 
Total Observations in Table:  497 

 
                   | subsample_whtn$ALCOHOL 
subsample_whtn$SEX |         0 |         1 | Row Total | 
-------------------|-----------|-----------|-----------|
                 0 |       122 |       124 |       246 | 
                   |     0.496 |     0.504 |     0.495 | 
                   |     0.589 |     0.428 |           | 
                   |     0.245 |     0.249 |           | 
-------------------|-----------|-----------|-----------|
                 1 |        85 |       166 |       251 | 
                   |     0.339 |     0.661 |     0.505 | 
                   |     0.411 |     0.572 |           | 
                   |     0.171 |     0.334 |           | 
-------------------|-----------|-----------|-----------|
      Column Total |       207 |       290 |       497 | 
                   |     0.416 |     0.584 |           | 
-------------------|-----------|-----------|-----------|

[R] 도수분포표 (Frequency table), 분할표 (Contingency table) 만들기 정복 완료!

작성일: 2022.08.31.

최종 수정일: 2022.08.31.

이용 프로그램: R 4.1.3

RStudio v1.4.1717

RStudio 2021.09.1+372 "Ghost Orchid" Release 

운영체제: Windows 10, Mac OS 10.15.7

[R] 도수분포표 (Frequency table), 분할표 (Contingency table) 만들기 - table(), prop.table(), xtabs(), margin.table()

 수천 명의 정보를 포함한 데이터를 한눈에 요약하고 싶을 때가 많다. 나이, 혈압과 같은 연속형 변수는 평균으로 요약하곤 하는데, 성별이나 음주 여부는 평균을 구할 수 없으니 빈도를 제시하곤 한다. 이를 표로 제시하면 도수분포표 (Frequency table)가 된다. 이를 넘어서 남성 중 음주자가 몇 명인지, 여성중 비음주자가 몇 명인지 알고 싶을 때가 있는데, 이때 사용하는 것이 분할표 (Contingency table)이다. 즉 본 글의 목적은 다음 두 개의 표 내용을 채우는 것이다.

<도수분포표>

<분할표>

R이 웬만한 프로그램보다 거의 모든 분야에서 분석하기엔 훨씬 편리하다. 하지만 오늘 다룰 도수분포표 및 분할표는 R이 압도적으로 불편하다. 그 불편한 분석을 오늘 해보고자 한다. (이런 이유로 CrossTable이라는 훌륭한 함수가 개발된 듯 하다. 다음 글로 소개하겠다. -2022.08.31 - [기술 통계/R] - [R] 도수분포표 (Frequency table), 분할표 (Contingency table) 만들기 - CrossTable())

*실습용 데이터는 아래 링크를 클릭하면 다운로드할 수 있습니다.

2022.08.04 - [공지사항 및 소개] - 분석용 데이터 (update 22.08.29)

코드를 보여드리기에 앞서 워킹 디렉토리부터 지정하겠다.

워킹 디렉토리에 관한 설명은 다음 링크된 포스트에서 볼 수 있다.

2022.08.05 - [통계 프로그램 사용 방법/R] - [R] 작업 디렉토리 (Working Directory) 지정 - getwd(), setwd()

setwd("C:/Users/user/Documents/Tistory_blog")

데이터를 불러와 df에 객체로 저장하겠다.

데이터 불러오는 방법은 다음 링크에서 볼 수 있다.

2022.08.05 - [통계 프로그램 사용 방법/R] - [R] 데이터 불러오기 : EXCEL - read_excel(), read.xlsx()

2022.08.10 - [통계 프로그램 사용 방법/R] - [R] 데이터 저장하기 : CSV 파일 - write.csv(), write_csv()

2022.08.10 - [통계 프로그램 사용 방법/R] - [R] 데이터 불러오기 : SAS file (.sas7bdat) - read.sas7bdat(), read_sas()

install.packages("readr")
library("readr")
df<-read_csv("Data.csv")

도수분포표

코드 - table() 

* 변수: SEX (성별)

  -0: 여성

  -1: 남성

table(df$SEX)

table(df$SEX) :df데이터에 있는 SEX변수로 도수분포표를 만들어라.

결과

  0   1 
482 518

해석

SEX(성별)이 0(여성)인 사람이 482명, 1(남성)인 사람이 518명이다.

하지만 앞으로 table()함수는 사용하지 않을 것이다. 왜냐하면, 보면 알겠지만 어떤 변수를 분석한 것인지 표시되지 않는다. 한 개의 변수를 분석할 때에는 문제가 되지 않겠지만 당장 분석하게 될 분할표에서는 2개 이상의 변수가 들어가는데, 어떤 변수가 행에 들어갔는지, 열에 들어갔는지 표시되지 않으므로 헷갈릴 때가 있기 때문이다.

코드 - xtabs() 

xtabs(~SEX, data=df)

xtabs(~SEX, data=df) : df라는 데이터에 있는 SEX로 도수분포표를 만들어라. 단, 도수는 정해져 있지 않다. 

도수란 무엇인가?

만약 데이터가 다음과 같다면 도수가 있는 데이터라고 할 수 있다.

이 데이터는

여성 & 음주자: 10명

여성 & 비음주자: 20명

남성 & 음주자: 20명

남성 & 비음주자: 50명

임을 의미한다. 즉 각 특성을 갖는 사람이 몇 명인지 알려주는 것인데 이런 변수가 있다면 코드 xtabs(~SEX, data=df) ~왼쪽에 N을 적어야 한다.

#만약 도수를 나타내는 변수가 있는 자료였다면?
xtabs(N~SEX, data=df)

위 코드는 가상의 코드임으로 구동되지 않는다.

결과

SEX
  0   1 
482 518

함수 xtabs()는 정말 고맙게도 변수의 이름을 표기해준다.

표의 다음 파란 글씨를 이제 채울 수 있게 되었다.

코드 - 분율

분율을 구하는 법은 다음과 같다.

prop.table(xtabs(~SEX, data=df))

prop.table(xtabs(~SEX, data=df)) :위에서 구한 도수분포표 [코드: xtabs(~SEX, data=df)]의 분율(proportion)을 구하라.

결과

SEX
    0     1 
0.482 0.518

SEX=0의 분율은 0.482, SEX=1의 분율은 0.518이다. 

하지만, %로 나타난 백분율이 아니므로 이대로는 표에 넣을 수 없다. 그리고 이런 식의 코드는 복잡함을 증대시키기 때문에 보통 다음과 같은 코드를 사용한다. 순서대로 설명하면 다음과 같다.

코드 - 백분율

freq_sex<-xtabs(~SEX, data=df)
prop_sex<-prop.table(freq_sex)
prop_sex_100<-100*prop_sex
prop_sex_100
round(prop_sex_100,digits=0)

freq_sex<-xtabs(~SEX, data=df) : 데이터 df안에 있는 변수 SEX의 도수분포표를 작성하여 freq_sex에 저장하라.

prop_sex<-prop.table(freq_sex)  : freq_sex의 분율을 구하여 prop_sex에 저장하라.
prop_sex_100<-100*prop_sex : prop_sex에 100을 곱하여 prop_sex_100에 저장하라

prop_sex_100 : prop_sex_100가 뭔지 보여달라.
round(prop_sex_100,digits=0) : prop_sex_100을 소수점 1번째 자리에서 반올림하여 정수로 보여달라

결과

SEX
   0    1 
48.2 51.8

SEX
 0  1 
48 52

위의 결과가 일반적인 백분율, 아래 결과는 정수로 반올림한 백분율을 나타낸다. 드디어 표의 두 번째 열을 채울 수 있게 되었다.

코드 - 누적 빈도, 누적 백분율

#누적 빈도 구하기
cumsum(freq_sex)

#누적 백분율 구하기
cumsum(prop_sex_100)

cumsum(freq_sex) : freq_sex (도수분포표)의 누적 도수를 구하라.
cumsum(prop_sex_100) : prop_sex_100 (백분율)로 누적 백분율을 구하라.

결과

   0    1 
 482 1000 
 
     0     1 
 48.2 100.0

이제 표를 완성할 수 있게 되었다.

도수분포표 코드 전체

#작업 디렉토리 지정
setwd("C:/Users/user/Documents/Tistory_blog")

#데이터 불러오기
install.packages("readr")
library("readr")
df<-read_csv("Data.csv")

#도수분포표
freq_sex<-xtabs(~SEX, data=df) 
freq_sex                       #빈도 
prop_sex<-prop.table(freq_sex) 
prop_sex_100<-100*prop_sex
prop_sex_100                   #백분율
round(prop_sex_100,digits=0)
cumsum(freq_sex)               #누적 빈도
cumsum(prop_sex_100)           #누적 백분율

분할표

분할표를 작성해보자. 코드는 다음과 같다.

코드 - 빈도

#각 셀의 빈도 구하기
freq_sex_alc<-xtabs(~SEX+ALCOHOL, data=df)
freq_sex_alc

#행 별로 합친 빈도 구하기
freq_sex<-margin.table(freq_sex_alc, margin=1)
freq_sex

#열 별로 합친 빈도 구하기
freq_alc<-margin.table(freq_sex_alc, margin=2)
freq_alc

#전체 데이터 수 구하기
total_freq_sex_alc<-sum(freq_sex_alc) #혹은 sum(freq_sex)이나 sum(freq_alc)도 가능
total_freq_sex_alc

freq_sex_alc<-xtabs(~SEX+ALCOHOL, data=df) : ( '+' 표시 앞에 있는) SEX를 세로축에, ('+' 표시 뒤에 있는) ALCOHOL을 가로축에 넣고 분할표를 만들고 freq_sex_alc에 저장하라. 이때 데이터는 df를 사용하라.
freq_sex_alc : 만든 분할표를 보여달라.
freq_sex<-margin.table(freq_sex_alc, margin=1) :행 별로 합친 도수분포표 만들고 freq_sex에 저장하라. 즉, 성별의 도수분포표를 보여달라는 뜻이고 본 데이터에는 결측치가 없으므로 이는 "xtabs(~SEX, data=df)"와 같은 결과를 보여준다. (결측치가 있으면 결과가 다를 수 있다.)
freq_sex : 성별의 도수분포표를 보여달라.
freq_alc<-margin.table(freq_sex_alc, margin=2) :열 별로 합친 도수분포표 만들고 freq_alc에 저장하라. 즉, 음주 여부의 도수분포표를 보여달라는 뜻이고 본 데이터에는 결측치가 없으므로 이는 "xtabs(~ALCOHOL, data=df)"와 같은 결과를 보여준다. (결측치가 있으면 결과가 다를 수 있다.)
freq_alc : 음주 여부의 도수분포표를 보여달라.

total_freq_sex_alc<-sum(freq_sex_alc) : 빈도를 모두 더해 total_freq_sex_alc에 저장하라.
total_freq_sex_alc :총빈도수를 보여달라.

결과

   ALCOHOL
SEX   0   1
  0 236 246
  1 174 344
  
SEX
  0   1 
482 518 

ALCOHOL
  0   1 
410 590

[1] 1000

xtabs()함수의 진가는 분할표를 만들 때에 나온다. table()함수에는 나오지 않는 각 변수명을 보여주니 말이다. 위 데이터로 표의 빈도를 채울 수 있게 되었다.

코드 - 백분율

#각 셀의 백분율
prop_sex_alc<-prop.table(freq_sex_alc)
prop_sex_alc_100<-100*prop_sex_alc
prop_sex_alc_100

#행 별로 합친 데이터의 백분율
prop_sex<-prop.table(freq_sex)
prop_sex_100<-100*prop_sex
prop_sex_100

#열 별로 합친 데이터의 백분율
prop_alc<-prop.table(freq_alc)
prop_alc_100<-100*prop_alc
prop_alc_100

#전체 데이터의 백분율
prop_total<-prop.table(total_freq_sex_alc)
prop_total_100<-100*prop_total
prop_total_100

prop_sex_alc<-prop.table(freq_sex_alc) :2*2 분할표에서 각 셀의 분율을 구하고 prop_sex_alc에 저장하라
prop_sex_alc_100<-100*prop_sex_alc : 분율에 100을 곱하여 백분율을 구하고 prop_sex_alc_100에 저장하라
prop_sex_alc_100 : 백분율을 보여달라

prop_sex<-prop.table(freq_sex) :행 별로 합친 데이터의 분율을 구하고 prop_sex에 저장하라
prop_sex_100<-100*prop_sex : 분율에 100을 곱하여 백분율을 구하고 prop_sex_100에 저장하라
prop_sex_100 : 백분율을 보여달라

prop_alc<-prop.table(freq_sex) :열 별로 합친 데이터의 분율을 구하고 prop_alc에 저장하라
prop_alc_100<-100*prop_alc : 분율에 100을 곱하여 백분율을 구하고 prop_alc_100에 저장하라
prop_alc_100 : 백분율을 보여달라

prop_total<-prop.table(total_freq_sex_alc) : 전체 데이터를 합쳤을 때 분율을 구하고 prop_total에 저장하라
prop_total_100<-100*prop_total :분율에 100을 곱하여 백분율을 구하고 prop_total_100에 저장하라
prop_total_100 : 백분율을 보여달라

결과

   ALCOHOL
SEX    0    1
  0 23.6 24.6
  1 17.4 34.4
  
SEX
   0    1 
48.2 51.8 

ALCOHOL
 0  1 
41 59

[1] 100

표의 백분율을 채울 수 있게 되었다.

백분율은 가로로 합하면 가로 합계의 백분율과 일치하고, 세로로 더하면 세로 합계의 백분율과 일치한다.

코드  - 행백분율

sum_row<-rowSums(freq_sex_alc)
prop_row<-freq_sex_alc/sum_row
prop_row_100<-100*prop_row
prop_row_100
round(prop_row_100, digits=2)

sum_row<-rowSums(freq_sex_alc) : 행 별로 더한 값을 sum_row에 저장한다. 즉 남성과 여성이 각각 몇 명이 있는지 보여준다. 이 값은 겉으로 보기엔 "freq_sex"와 같다. 하지만 속성이 약간 다르며 freq_sex로 대체할 수 없다.
prop_row<-freq_sex_alc/sum_row : 각 셀의 빈도를 행별로 더한 값으로 나눈다. 즉, 음주자건 비음주자건 남성이면 남성의 수로 나누고, 여성이면 여성의 수로 나눈다. 그리하여 분율을 구한다.
prop_row_100<-100*prop_row : 분율에 100을 곱해 백분율을 구한다. 
prop_row_100 : 백분율을 보여달라.

round(prop_row_100, digits=2) : 소수점 셋째 자리에서 반올림하여 둘째 자리까지만 표기하라.

결과

   ALCOHOL
SEX        0        1
  0 48.96266 51.03734
  1 33.59073 66.40927
  
   ALCOHOL
SEX     0     1
  0 48.96 51.04
  1 33.59 66.41

반올림한 결과가 훨씬 보기 편한 걸 알 수 있다. 그리고 가로로 합하면 100이 나오는 것을 볼 수 있다.

표의 행백분율을 채울 수 있게 되었다.

코드 - 열백분율

R 특성상 조금 더 복잡해진다.

sum_col<-colSums(freq_sex_alc)
prop_col<-t(t(freq_sex_alc)/sum_col)
prop_col_100<-100*prop_col
prop_col_100
round(prop_col_100, digits=2)

sum_col<-colSums(freq_sex_alc) : 열 별로 더한 값을 sum_col에 저장한다. 즉 음주자와 비음주자가 각각 몇 명이 있는지 보여준다. 이 값은 겉으로 보기엔 "freq_alc"와 같다. 하지만 속성이 약간 다르며 freq_alc로 대체할 수 없다.
prop_col<-t(t(freq_sex_alc)/sum_col) : R에서 나눌 때에는 행 별로 나눈다. 즉 열 별로 나누려면 행/열을 바꾼 다음에 나누어야 한다. 어려운 말로 전치 행렬을 구해야 한다는 것이고 전치 행렬을 구하는 명령어가 t()다. 나눈 다음에 다시 한번 행/열을 바꾸지 않으면 세로에 음주 여부, 가로에 성별에 들어가 있으므로 보기에 편하려면 다시 한번 전치 행렬을 구해야 한다.
prop_col_100<-100*prop_col : 분율에 100을 곱해 백분율을 구한다. 
prop_col_100 : 백분율을 보여달라.
round(prop_col_100, digits=2) : 소수점 셋째 자리에서 반올림하여 둘째 자리까지만 표기하라.

결과

   ALCOHOL
SEX        0        1
  0 57.56098 41.69492
  1 42.43902 58.30508
  
   ALCOHOL
SEX     0     1
  0 57.56 41.69
  1 42.44 58.31

표를 완성할 수 있다.

분할표 코드 전체

#작업 디렉토리 지정
setwd("C:/Users/user/Documents/Tistory_blog")

#데이터 불러오기
install.packages("readr")
library("readr")
df<-read_csv("Data.csv")

########빈도########

#각 셀의 빈도 구하기
freq_sex_alc<-xtabs(~SEX+ALCOHOL, data=df)
freq_sex_alc

#행 별로 합친 빈도 구하기
freq_sex<-margin.table(freq_sex_alc, margin=1)
freq_sex

#열 별로 합친 빈도 구하기
freq_alc<-margin.table(freq_sex_alc, margin=2)
freq_alc

#전체 데이터 수 구하기
total_freq_sex_alc<-sum(freq_sex_alc) #혹은 sum(freq_sex)이나 sum(freq_alc)도 가능
total_freq_sex_alc



########백분율########

#각 셀의 백분율
prop_sex_alc<-prop.table(freq_sex_alc)
prop_sex_alc_100<-100*prop_sex_alc
prop_sex_alc_100

#행 별로 합친 데이터의 백분율
prop_sex<-prop.table(freq_sex)
prop_sex_100<-100*prop_sex
prop_sex_100

#열 별로 합친 데이터의 백분율
prop_alc<-prop.table(freq_alc)
prop_alc_100<-100*prop_alc
prop_alc_100

#전체 데이터의 백분율
prop_total<-prop.table(total_freq_sex_alc)
prop_total_100<-100*prop_total
prop_total_100


########행백분율########

sum_row<-rowSums(freq_sex_alc)
prop_row<-freq_sex_alc/sum_row
prop_row_100<-100*prop_row
prop_row_100
round(prop_row_100, digits=2)


########열백분율########

sum_col<-colSums(freq_sex_alc)
prop_col<-t(t(freq_sex_alc)/sum_col)
prop_col_100<-100*prop_col
prop_col_100
round(prop_col_100, digits=2)

세 개 이상의 변수를 사용하는 분할표

코드

freq_sex_alc_htn<-xtabs(~SEX+ALCOHOL+HTN, data=df)
freq_sex_alc_htn

freq_sex_alc_htn<-xtabs(~SEX+ALCOHOL+HTN, data=df) : 데이터는 df를 사용하되 세로축에 SEX, 가로축에 ALCOHOL을 놓는다. HTN 값 별로 분할표를 각각 만들어 freq_sex_alc_htn에 저장한다.
freq_sex_alc_htn : 각각의 분할표를 보여달라.

결과

, , HTN = 0

   ALCOHOL
SEX   0   1
  0 114 122
  1  89 178

, , HTN = 1

   ALCOHOL
SEX   0   1
  0 122 124
  1  85 166

고혈압이 없는 (HTN=0) 사람들과 고혈압이 있는 (HTN=1) 사람들의 분할표를 각각 보여준다. 인구를 고혈압뿐만 아니라 RH혈액형으로도 나누고 싶다면 HTN뒤에 "+RH"를 붙여 다음과 같은 코드를 쓰면 된다.

#코드
freq_sex_alc_htn_rh<-xtabs(~SEX+ALCOHOL+HTN+RH, data=df)
freq_sex_alc_htn_rh

#결과
, , HTN = 0, RH = 0

   ALCOHOL
SEX   0   1
  0   0   0
  1   2   2

, , HTN = 1, RH = 0

   ALCOHOL
SEX   0   1
  0   1   0
  1   1   0

, , HTN = 0, RH = 1

   ALCOHOL
SEX   0   1
  0 114 122
  1  87 176

, , HTN = 1, RH = 1

   ALCOHOL
SEX   0   1
  0 121 124
  1  84 166

SAS에는 인구를 나누는 변수를 맨 앞에 쓰지만, R에서는 맨 뒤에 쓴다는 것을 유의해야 한다.

SAS에서의 분할표 작성법:

2022.08.18 - [기술 통계/SAS] - [SAS] 도수분포표 (Frequency table), 분할표 (Contingency table) 만들기 - PROC FREQ

결론적으로 R로 분할표를 만드는 것은 매우 귀찮은 일이기 때문에 SPSS나 SAS를 쓰거나 CrossTable()함수를 쓰길 권한다.

2022.08.31 - [기술 통계/R] - [R] 도수분포표 (Frequency table), 분할표 (Contingency table) 만들기 - CrossTable()

[R] 도수분포표 (Frequency table), 분할표 (Contingency table) 만들기 정복 완료!

작성일: 2022.08.31.

최종 수정일: 2022.08.31.

이용 프로그램: R 4.1.3

RStudio v1.4.1717

RStudio 2021.09.1+372 "Ghost Orchid" Release 

운영체제: Windows 10, Mac OS 10.15.7

[SAS] 연속성 수정 카이 제곱 검정 (Yates's correction for continuity) - PROC FREQ

본 글은 기존 카이 제곱 검정 포스팅의 후속 포스팅이므로 다음 글을 미리 읽고 오길 권한다.

2022.08.19 - [범주형 자료 분석/SAS] - [SAS] 카이 제곱 검정 - PROC FREQ

 도수분포표에 들어가는 숫자는 '정수'인 이산 변수인데 카이 제곱 분포에는 연속 변수가 사용된다. 이산 분포를 연속 분포에 근사하면서 발생하는 문제를 해결하기 위해 고안된 것이 "연속성 수정(Yates's correction for continuity)"이다. 쉽게 말해 20대 성인의 평균 나이는 20살이 아니라 25살이라고 보는 것이 합당하다는 이야기인데, 더 자세한 내용이 알고 싶은 독자들은 이전 포스팅을 참고하길 바란다.

2022.08.30 - [통계 이론] - [이론] 연속성을 수정한 카이 제곱 검정 (Chi-squared test with Yates's correction for continuity)

*실습용 데이터는 아래 링크를 클릭하면 다운로드할 수 있습니다.

2022.08.04 - [공지사항 및 소개] - 분석용 데이터 (update 22.08.29)

시작하기 위해 라이브러리를 만들고, 파일을 불러온다.

라이브러리 만드는 방법: 2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 라이브러리 만들기 - LIBNAME

파일 불러오는 방법: 2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 데이터 불러오기 및 저장하기 - PROC IMPORT, PROC EXPORT

*라이브러리 지정하기;
LIBNAME hong "C:/Users/User/Documents/Tistory_blog";

*파일 불러오기;
PROC IMPORT
DATAFILE="C:\Users\user\Documents\Tistory_blog\Data.xlsx"
DBMS=EXCEL
OUT=hong.df
REPLACE;
RUN;

코드

연속성을 수정한 카이 제곱 검정을 시행하는 코드는 다음과 같다. (일반 카이 제곱 검정과 100% 일치한다)

PROC FREQ DATA=hong.df;
TABLE SEX*ALCOHOL/CHISQ NOFREQ NOPERCENT NOROW NOCOL EXPECTED;
RUN;

PROC FREQ DATA=hong.df; 분할표 분석을 시작하고 Data는 hong 라이브러리의 df 파일을 이용한다.
TABLE SEX*ALCOHOL/CHISQ NOFREQ NOPERCENT NOROW NOCOL EXPECTED; : SEX와 ALCOHOL의 분할표를 작성하고 카이제곱 검정을 시행한다. 빈도, 백분율, 행백분율, 열백분율은 나타내지 말고 기댓값(기대 빈도)을 나타낸다. 

결과

해석

 모든 셀에서 기대 빈도가 5 이상이므로 카이 제곱 검정을 시행하는 데에 문제가 없다.

 연속성 수정한 카이 제곱 검정 결과 p-value <0.0001으로 성별과 음주 여부에는 유의미한 관계가 있다. 

 일반적인 카이 제곱 검정량 (24.3892) 보다 낮아 보수적인 통계량임을 알 수 있다.

SAS 연속성 수정 카이 제곱 검정 (Yates's correction for continuity) 정복 완료!

작성일: 2022.08.30.

최종 수정일: 2022.08.30.

이용 프로그램: SAS v9.4

운영체제: Windows 10

[이론] 연속성을 수정한 카이 제곱 검정 (Chi-squared test with Yates's correction for continuity)

이 글을 읽기 전에 이전 포스팅을 읽고 오길 권한다.

2022.08.29 - [통계 이론] - [이론] 카이 제곱 검정과 피셔 정확 검정의 관계

범주형 자료를 분석할 때 카이 제곱 검정을 많이 사용하곤 한다. 하지만 카이 제곱 검정에는 치명적인 단점이 존재한다. 이는 이산 분포인 초기하 분포를 연속형 분포인 카이 제곱 분포에 근사하는 과정에서 발생한다. 

이산형 변수 = 소수점이 없는 변수

 이산형 변수는 쉽게 말해 소수점 아래 데이터가 없는 변수다.

 예를 들어 30살인 사람 11명이 모여있을 때 이 사람들의 평균 나이는 어떻게 될까? 모두 30살이므로 평균도 30이라고 할 수 있을까? 도대체 30살이라는 것이 무엇인가?

 30살인 사람은 30년 0일을 산 사람부터 30년 364일 23시간 59분 59초 9999.. 를 산 사람까지를 아우르는 말이다. 일상적으로 내가 $x$살 $y$개월을 살았어도 모두들 $x$살 살았다고 표현한다. 그런데 소수점 이하 숫자를 버린다면 과소평가 (underestimation)하게 된다.  가상의 11명의 나이를 반올림해보기도 하고 버림을 해보기도 하면 다음과 같다.

 반올림을 하면 10명 중 절반 정도는 "억울하게" 더 많은 나이를 갖게 되고 (과대평가), 나머지 절반 정도는 "운이 좋게" 더 어린 나이를 갖게 된다 (과소평가). 그래서 나이의 평균과 반올림 나이의 평균은 거의 일치한다. 하지만 버림을 한 나이는 누구나 "운이 좋게" 어린 나이를 갖게 되므로 (과소평가) 평균은 항상 참값보다 적게 나오게 된다. 

Yates의 의문점

 그렇다면 "Yates"가 제기한 의문은 이것이다.

"버림을 시행한 자료가 원자료를 대표한다고 할 수 있겠는가?"

해결

해결은 두 가지 논리로 설명해 보겠다. 결론은 같으나 함의가 다르니 찬찬히 살펴보길 바란다.

방법 (1) - 분할표는 버림이 된 상태다!

 흡연자이자 폐암 환자인 사람은 30명이었다고 하자. 하지만, 만약 전체 인구가 10,000명이었다면 어땠을까? 폐암 환자이면서 흡연자인 사람은 300명일 수도 있고, 301명, 302,... , 309명 일 수도 있었을 것이다. 그런데 1,000명만 뽑으면서 흡연자이자 폐암 환자인 사람은 30명이 뽑힐 수도 있고, 30.1명이 뽑힐 수도 있고, 30.2, 30.3,..., 30.9명이 뽑힐 수도 있었다. 이 상황에서 깔끔히 버림을 하고 30이라고 적자고 합의를 한 것이다. 

 그러면 폐암 환자이자 흡연자인 "30명"이라는 값은 $30\leq x<31$을 대표하는 값이다. 근사하기 전 분포인 초기하 분포는 이산 분포이므로 30 다음의 숫자는 31이다. 하지만 근사 시킨 카이 제곱 분포는 연속 분포이므로 30 다음의 숫자가 31이 아니다. 30부터 31 사이에는 수많은 숫자가 존재한다. 따라서 여기에는 $30\leq x <31$라는 숫자가 존재하므로 $30\leq x <31$의 숫자를 대표하는 숫자로 "30명"을 쓰는 것은 적절하지 않다. 그 중간값인 "30.5명"을 쓰는 것이 더욱 적절하다. 그리하여 카이 제곱 통계량 계산 식이 다음과 같이 바뀌는 것이다.

$$\chi^{2} _{Yates}=\sum_{ij} \frac{\left( \lvert a_{ij}-e_{ij}\rvert-0.5 \right)^{2}}{e_{ij}}$$

아마 Yates가 의도한 연속성 수정 (Correction for contunuity)이라는 말은 여기에서 기인한 것일 거다.

하지만 결론적으로 연속성 수정한 카이 제곱 검정은 현실적으로 쓰이고 있지 않은데, 아마 다음의 이유 때문일 것이다.

방법 (2) - 분할표는 반올림이 된 상태다!

 버림이 된 상황이라고 가정한 것은 순전히 위 상황을 합리화하기 위한 것이었다. 세상 대부분의 일은 반올림이 시행된다.   예를 들어 소수점 첫째 자리까지 표기할 수 있는 디지털 체중계가 75.3kg을 나타냈다고 하자. 이 사람의 실제 몸무게는 $75.25\leq 몸무게<75.35$ 사이에 있다고 보는 것이 적당할 것이다.

 분할표에 있는 숫자 또한 반올림이 된 상태라는 가정 하에 다시 분할표를 살펴보자. 폐암 환자이자 흡연자인 사람의 수 "30명"이 나타내는 것은 $29.5\leq x<30.5$을 나타내는 숫자다. 그런데 "30명"이라는 숫자로 구한 카이 제곱 검정의 p-value는 30명이 발생하는 것보다 일어나기 어려운 사건들이 일어날 확률을 의미한다. 여기에서 기대 빈도는 60명이므로 60 이하에서는 관찰 빈도가 낮아진다는 것은 일어나기 어려운 상황을 의미한다. 따라서 $29.5\leq x \leg30$이 발생할 확률은 "30명"이라는 숫자로 구한 카이 제곱 검정의 p-value에 포함되어 있다. 하지만 $30<x<30.5$는 포함되지 못한다. 그런데 위에서 구한 식 

$$\chi^{2} _{Yates}=\sum_{ij} \frac{\left( \lvert a_{ij}-e_{ij}\rvert-0.5 \right)^{2}}{e_{ij}}$$

을 쓴다는 것은 다음을 의미한다.

"30이라는 숫자에는 $30<x<30.5$가 발생할 가능성도 내포하고 있는 것이다. 혹시 모르니까 30이 아닌 30.5로 계산하자."

따라서 p-value가 더 커지게 되고 보수적인 계산을 하게 되는 것이다.

그런데 왜 절댓값 기호가 붙었는지 이해하기 위해 다음 내용을 봐보자.

여기에서 2*2 분할표가 위와 같을 때 이 데이터로 구하는 카이 제곱 통계량의 의미를 다시 생각해보자.

 - 폐암 환자이면서 흡연자의 기대 빈도는 60명이다. 

 - 폐암 환자이면서 흡연자인 사람이 30명인 사건이 발생했다.

 - p-value는 "이 정도의 일이 발생할 확률이 얼마인가?"를 의미하는 것이다.

따라서, p-value를 구하기 위해서는 30명이 발생할 확률만 알아서는 안 된다.

 - 30명이 발생하는 것보다 일어나기 어려운 사건들의 확률을 모두 합해야 한다.

 - 기대 빈도인 60명이 발생할 확률이 가장 크고, 60에서 멀어질수록 확률은 낮아진다.

 (1) 30명보다 작은 경우 

   - 29명이 발생할 확률은 더 낮을 것이므로 더해야 한다.

   - 28, 27,... , 1, 0명이 발생할 확률은 더 낮으므로 모두 더해야 한다.

 (2) 30명보다 큰 경우 

   - 30명보다 커지는 상황을 상상해볼 때 60명이 될 때까지는 확률이 증가하다가 그 이후로 감소한다.

   - 하필이면 30명일 확률과 정확히 똑같아지는 시점은 90명일 때다. (계산을 해보면 알 수 있다.)

   - 따라서 90명일 발생할 확률, 91, 92,..., 199, 200명이 발생할 확률을 모두 더해야 한다.

"(1) 30명보다 작은 경우" 30이 아닌 30.5를 쓰는 이유는 위에서 모두 설명이 되었다,

"(2) 30명보다 큰 경우"에 대해 설명을 하겠다.

예를 들어 90이라는 숫자에는 $89.5\leq x<90.5$가 포함되어 있는 것이다. 그런데 $90\leq x<90.5$는 이미 카이 제곱 검정 계산에 포함되어 있다. 하지만 $89.5\leq x<90$은 포함되어 있지 않으므로 "89.5"를 기준으로 계산해야 한다는 것이 Yates의 논리다. 그가 의도했든 의도하지 않았든 말이다. 즉, 기댓값보다 작을 때에는 0.5를 더하고, 기댓값보다 클 때에는 0.5를 빼는 로직을 만들어야 하는데, 이를 수식으로 한 번에 나타내는 방법이 절댓값 기호를 붙이는 것이다.

하지만, 결국 Yates의 연속성 수정은 너무나 보수적이고, 학자들 사이에서도 의견이 분분하여 굳이 쓰이지 않고 있는 분석 방법이다.

[이론] 연속성을 수정한 카이 제곱 검정 (Chi-squared test with Yates's correction for continuity) 정복 완료!

작성일: 2022.08.30.

최종 수정일: 2022.08.30.

[SAS] 피셔 정확 검정 - PROC FREQ

범주형 변수 간에 분포에 차이가 있는지 확인하기 위해서는 보통 카이 제곱 검정을 시행한다 (2022.08.19 - [범주형 자료 분석/SAS] - [SAS] 카이 제곱 검정 - PROC FREQ). 하지만 기대 빈도가 5 미만인 셀이 25% 이상인 경우 카이 제곱 검정의 결과는 신뢰도가 떨어지기 때문에 피셔 정확 검정 (Fisher's exact test)을 시행해야 한다.

 참고로, 피셔 "정확" 검정인 이유는, 말 그대로 정확한 확률이기 때문이고, 어떤 분포에 근사시키지 않았다는 말이다. 

*실습용 데이터는 아래 링크를 클릭하면 다운로드할 수 있습니다.

2022.08.04 - [공지사항 및 소개] - 분석용 데이터 (update 22.08.29)

시작하기 위해 라이브러리를 만들고, 파일을 불러온다.

라이브러리 만드는 방법: 2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 라이브러리 만들기 - LIBNAME

파일 불러오는 방법: 2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 데이터 불러오기 및 저장하기 - PROC IMPORT, PROC EXPORT

*라이브러리 지정하기;
LIBNAME hong "C:/Users/User/Documents/Tistory_blog";

*파일 불러오기;
PROC IMPORT
DATAFILE="C:\Users\user\Documents\Tistory_blog\Data.xlsx"
DBMS=EXCEL
OUT=hong.df
REPLACE;
RUN;

2*2 분할표

코드

피셔 정확 검정을 시행하는 코드는 다음과 같다.

PROC FREQ DATA=hong.df;
TABLE SEX*RH/CHISQ EXPECTED NOROW NOCOL NOPERCENT;
RUN;

PROC FREQ DATA=hong.df; : 빈도수를 계산하는 코드를 시작하며, 데이터는 hong 라이브러리의 df 파일을 이용한다.
TABLE SEX*RH/CHISQ EXPECTED NOROW NOCOL NOPERCENT; : SEX와 RH의 분할표를  계산하며, 카이 제곱 검정을 시행한다. 기대 빈도를 산출하고, 행 백분율, 열 백분율, 백분율은 산출하지 않는다.

"CHISQ" 옵션이 자동으로 피셔 정확 검정 결과까지 산출하므로 카이 제곱 검정을 시행하는 코드와 100% 일치한다. 즉, 굳이 피셔 정확 검정을 시행하는 옵션인 "FISHER"를 적을 필요가 없다.

결과

먼저 기대 빈도 (기댓값)를 산출했는데 기대 빈도가 5 미만인 셀이 두 개가 있다. (2.892와 3.108) 따라서 경고가 뜬다. "WARNING: 50% 개의 셀이 5보다 적은 기대 빈도를 가지고 있습니다. 카이제곱 검정은 올바르지 않을 수 있습니다."즉, 카이제곱 분포가 아닌 아래 나오는 "Fisher의 정확 검정" 표를 참고하라는 말이다.

세 개의 p-value가 산출된다. 1) 하단측 p값 Pr<=F2) 상단측 p값 Pr>=F3) 양측 p값 Pr<=P

1)과 2)는 단측 검정 (One-sided or One-tailed)이고 3)은 양측 검정 (Two-sided or two-tailed)이다. 경우에 따라 단측 검정을 쓰기도 하지만 일반적으로는 양측 검정을 사용한다. 이 p-value는 0.2192로 0.05보다 크므로 귀무가설을 기각하지 못해 "성별에 따라 RH 혈액형의 분포에는 차이가 있다고 할 수 없다."라고 결론이 내려진다. 양측 검정 및 단측 검정에 관한 내용은 다음 글을 확인하길 바란다:2022.08.26 - [통계 이론] - [이론] 피셔 정확 검정 (Fisher's exact test)

2*2를 넘어서는 분할표

코드

피셔 정확 검정을 시행하는 코드는 다음과 같다.

PROC FREQ DATA=hong.df;
TABLE SEX*TWIN/CHISQ EXACT EXPECTED NOROW NOCOL NOPERCENT;
RUN;

PROC FREQ DATA=hong.df; : 빈도수를 계산하는 코드를 시작하며, 데이터는 hong 라이브러리의 df 파일을 이용한다.
TABLE SEX*TWIN/CHISQ EXACT EXPECTED NOROW NOCOL NOPERCENT; : SEX와 TWIN의 분할표를  계산하며, 카이 제곱 검정을 시행한다. 정확 검정도 시행한다. 기대 빈도를 산출하고, 행 백분율, 열 백분율, 백분율은 산출하지 않는다.

2*2 분할표에서만 "CHISQ" 옵션이 자동으로 피셔 정확 검정 결과까지 산출해준다. 따라서 2*2를 넘어서는 분할표에서는 정확 검정을 시행하는 "EXACT"혹은 "FISHER"를 적어야 한다. "FISHER"라는 코드로 검정을 시행하고 결과창에도 "Fisher의 정확 검정"이라고 적혀 있지만 이는 사실 "Freeman-Halton test"다.

결과

2*2 분할표 분석에서 보이는 바와 거의 같은 결과를 내주지만 "Fisher의 정확 검정"에는 양측 검정 결과만이 나온다. 빨간 상자에 있는 값이 p-value다. p>0.05이므로 "성별에 따라 쌍둥이 여부는 어떠한 경향성을 갖는다고 할 수 없다."라고 결론짓게 된다.

피셔 정확 검정의 이론적 배경

2022.08.26 - [통계 이론] - [이론] 피셔 정확 검정 (Fisher's exact test)

카이 제곱 검정과 피셔 정확 검정의 관계

2022.08.29 - [통계 이론] - [이론] 카이 제곱 검정과 피셔 정확 검정의 관계

SAS 피셔 정확 검정 정복 완료!

작성일: 2022.08.29.

최종 수정일: 2022.08.29.

이용 프로그램: SAS v9.4

운영체제: Windows 10

[이론] 카이 제곱 검정과 피셔 정확 검정의 관계

 범주형 자료 분석을 할 때 "기대 빈도가 5 미만인 셀이 25% 이상인 경우 카이 제곱 검정을 신뢰할 수 없으며 피셔 정확 검정의 결과를 확인해야 한다."라는 말을 정말 많이 보게 된다. 도대체 카이 제곱 검정과 피셔 정확 검정이 무슨 관계이길래 이렇다는 건지 궁금증이 유발될 것이다. 모든 것을 설명할 수는 없지만, 왜 이런 이야기들이 나오는지 대략적으로 설명하고자 한다.

본 글을 읽기 전에 카이 제곱 검정과 피셔 정확 검정의 이론 내용에 관한 포스트를 읽고 오기를 강력히 권한다.

카이 제곱 검정: 2022.08.16 - [통계 이론] - [이론] 카이 제곱 검정 (Chi-squared test)

피셔 정확 검정: 2022.08.26 - [통계 이론] - [이론] 피셔 정확 검정 (Fisher's exact test)

카이 제곱 검정=근사, 피셔 정확 검정=정확

먼저 이해해야 하는 것은 "왜 카이 제곱 검정을 쓰게 되었는가?"일 것이다. 결론적으로는 정확한 방법인 피셔 정확 검정 시 계산량이 너무 방대하여 그에 근사하는 카이 제곱 분포를 사용했다는 것이다.

 물론 Pearson 경이 어떤 생각으로 카이 제곱 검정을 만들었는지 정확하게 알 수는 없을 뿐 아니라, 그나마 세간에 알려진 이유도 나에게는 그다지 와닿지는 않는다. 피어슨 경의 생각을 읽어보면 아마도 다음과 같을 것이다. (따라서 본 포스팅은 문헌을 리뷰하거나 참고한 것이 아니며 피어슨 입장에서 생각해본 '뇌피셜'이다.)

분포가 무엇인지 대충이라도 상상해보기

흡연과 폐암의 빈도 표가 다음과 같다고 하자.

각 셀 안의 값은 정확히 모르지만 빨간색으로 표시된 총합의 값은 정확히 알려져 있다고 하자. 이때 (A)에 들어갈 수 있는 숫자는 이론적으로 0부터 200 사이의 값이다. 흡연과 폐암에 아무런 관련성이 없을 때 (A)에 들어갈 것으로 생각되는 숫자를 생각해보자. 폐암은 흡연과 관련이 없고, 전체 인구 중 흡연자는 30%를 차지하므로 폐암 환자 200명 중 30%인 60명이 있을 것으로 기대된다. 당연하게도 60명이 있을 확률이 가장 높아야 하고, 60보다 커지거나 작아질수록 그 확률은 감소해야 한다. 따라서 확률 분포 함수는 다음과 같을 것이다.

대립 가설 검정하기 <흡연자일수록 폐암환자일 가능성이 높아지는 관련성이 있다.>  (One-sided, One-Tailed)

실제로 관찰 빈도가 다음과 같았다고 하자.

 아무런 관련성이 없었다면 폐암 환자이면서 흡연자일 것으로 예상되는 사람의 수는 60명이었는데 75명이 관찰되었으므로 흡연자일수록 폐암환자일 가능성이 높아질 것이라고 예상해볼 수 있다. 이것이 통계적으로 유의미한지 확인하는 사고 과정은 다음과 같다.

"흡연자이면서 폐암환자로 예상된 사람은 60명이었는데 75명이나 있네?"

$\rightarrow$ "이 말은 폐암과 흡연이 관련성이 있다는 것 아닐까?"

$\rightarrow$  [가정] "흡연이랑 폐암 간에 아무런 관계가 없다고 가정해보자."

$\rightarrow$ "그런 가정 하에서 흡연자이면서 폐암환자인 사람이 75명 이상일 확률이 얼마인지 구해보자."

계산 방법: 아래 수식을 모두 합한다.

$$75명일 확률 = \frac{\begin{pmatrix} 300 \\  75 \end{pmatrix} \times \begin{pmatrix} 700 \\  125 \end{pmatrix}} {\begin{pmatrix} 1000 \\  200 \end{pmatrix}}$$

$$76명일 확률 = \frac{\begin{pmatrix} 300 \\  76 \end{pmatrix} \times \begin{pmatrix} 700 \\  124 \end{pmatrix}} {\begin{pmatrix} 1000 \\  200 \end{pmatrix}}$$

$$77명일 확률 = \frac{\begin{pmatrix} 300 \\  77 \end{pmatrix} \times \begin{pmatrix} 700 \\  123 \end{pmatrix}} {\begin{pmatrix} 1000 \\  200 \end{pmatrix}}$$

$$\vdots$$

$$200명일 확률 = \frac{\begin{pmatrix} 300 \\  200 \end{pmatrix} \times \begin{pmatrix} 700 \\  0 \end{pmatrix}} {\begin{pmatrix} 1000 \\  200 \end{pmatrix}}$$

위 값들을 모두 더하면 0.00674213이다.

$\rightarrow$ "이 정도의 확률은 현실적에서 일어나기는 어려운 일 아니야?"

$\rightarrow$ "그러면 차라리 흡연자일수록 폐암에 걸릴 확률이 높은 게 진실이고 그런 현실 속에서 발생한 일이라고 보는 게 낫겠다."

위 사고 구조의 비현실성: 방대한 계산량

 위 사고 과정은 틀린 것이 없고 논리적이기만 하다. 하지만 피어슨(Pearson) 경이 활동했을 1900년 경에는 복잡한 계산을 순식간에 해줄 계산기가 없었기 때문에, "75명일 확률", "76명일 확률", "77명일 확률",... , "200명일 확률"을 일일이 계산한다는 것은 굉장히 귀찮고 시간이 많이 걸리지만 그에 비해 그만한 가치는 별로 없는 일이었을 것이다.

 예를 들어 "75명일 확률"만 하더라도 

$$75명일 확률 = \frac{\begin{pmatrix} 300 \\  75 \end{pmatrix} \times \begin{pmatrix} 700 \\  125 \end{pmatrix}} {\begin{pmatrix} 1000 \\  200 \end{pmatrix}}= \frac {\frac {300!} {75! \times 225!}\times \frac {700!} {125! \times 575!}} { \frac {1000!} {200! \times 800!}} $$

와 같은데, 저 계산을 한다는 것은 아주 매우 많이 귀찮은 일일 것이다.

근사하는 분포를 만들자

 그래서 피어슨 경은 초기하 분포 (hypergeometric distribution)를 계산이 이미 되어있는 어떤 분포에 근사 시키고자 하는 욕구가 들었을 것이다. 아마도 피어슨 경은 두 번의 근사를 통해 초기하 분포를 정규분포에 근사 시키고자 했을 것이다.

 1) 초기하 분포 (hypergeometric distribution)에서 이항 분포(binomial distribution)로

 2) 이항 분포 (binomial distribution)에서 정규 분포 (normal distribution)로

 1) 초기하 분포 (hypergeometric distribution)에서 이항 분포(binomial distribution)로

위와 같은 상황에서 다음 조건을 만족하면 초기하 분포는 이항 분포로 근사 시킬 수 있다.

$$K>0.1 \times N$$

 2) 이항 분포 (binomial distribution)에서 정규 분포 (normal distribution)로

어떤 이항 분포의 시행 횟수가 $n$, 발생 확률이 $p$일 때, $np>5, n(1-p)>5$이면 이항 분포는 정규 분포로 근사될 수 있다. 

여기에서 $np$와 $n(1-p)$는 각각 사건이 일어나 기댓값과 일어나지 않을 기댓값을 의미한다. "기대 빈도가 5 미만인 셀이 25% 이상인 경우 카이 제곱 검정을 신뢰할 수 없으며 피셔 정확 검정의 결과를 확인해야 한다."라는 말은 여기에서 기인한 것으로 보인다.

근사하는 정규분포를 지정하자

 정규 분포의 확률 밀도 함수 (probability density function)은 다음과 같다.

$$ {\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}$$

갑자기 수식 이야기를 왜 하느냐? 

 수식을 보면 정규 분포를 정의하는 데에 오직 평균($\mu$)과 표준편차($\sigma$)만이 필요하다는 것을 알 수 있다. 즉, 초기하 분포의 평균과 표준편차 (혹은 분산)를 알아내면 근사하는 정규분포를 지정할 수 있다.

(1) 평균

초기하 분포 (hypergeometric distribution)의 이산 밀도 함수 (discrete density function)은 $$f_{k} (k;K,N,n)= \frac{\begin{pmatrix} K \\  k \end{pmatrix} \times \begin{pmatrix} N-K \\  n-k \end{pmatrix}} {\begin{pmatrix} N \\  n \end{pmatrix}}$$ 이므로 평균($\mu$)은 다음과 같이 구할 수 있다.

$$\begin{align}  \mu &=\sum _{k} {k \times \frac{\begin{pmatrix} K \\  k \end{pmatrix} \times \begin{pmatrix} N-K \\  n-k \end{pmatrix}} {\begin{pmatrix} N \\  n \end{pmatrix}} } \\&=\sum _{k} {K \times \frac{\begin{pmatrix} K-1 \\  k-1 \end{pmatrix} \times \begin{pmatrix} N-K \\  n-k \end{pmatrix}} {\begin{pmatrix} N \\  n \end{pmatrix}} } \\&=\sum _{k} {K \times \frac{\begin{pmatrix} K-1 \\  k-1 \end{pmatrix} \times \begin{pmatrix} N-K \\  n-k \end{pmatrix}} {\frac{N}{n} \times \begin{pmatrix} N-1 \\  n-1 \end{pmatrix}} } \\&= \frac {Kn} {N} \\&&\end{align} $$

(2) 분산

분산은 다음과 같이 계산할 수 있다.

$$ \begin{align} \sigma^{2}&=\sum _{k} {k^{2} \times \frac{\begin{pmatrix} K \\  k \end{pmatrix} \times \begin{pmatrix} N-K \\  n-k \end{pmatrix}} {\begin{pmatrix} N \\  n \end{pmatrix}} }  - \mu^{2} \\ &=\sum _{k} {Kk\times \frac{\begin{pmatrix} K-1 \\  k-1 \end{pmatrix} \times \begin{pmatrix} N-K \\  n-k \end{pmatrix}} {\begin{pmatrix} N \\  n \end{pmatrix}} }  - \left( \frac {Kn} {N} \right)^{2} \\& =K \left( \sum _{k} { \left(k-1\right)\times \frac{\begin{pmatrix} K-1 \\  k-1 \end{pmatrix} \times \begin{pmatrix} N-K \\  n-k \end{pmatrix}} {\begin{pmatrix} N \\  n \end{pmatrix}} }  + \sum _{k} { \times \frac{\begin{pmatrix} K-1 \\  k-1 \end{pmatrix} \times \begin{pmatrix} N-K \\  n-k \end{pmatrix}} {\begin{pmatrix} N \\  n \end{pmatrix}} } \right)  - \left( \frac {Kn} {N} \right)^{2} \\&=K \left( \sum _{k} { \left(K-1\right)\times \frac{\begin{pmatrix} K-2 \\  k-2 \end{pmatrix} \times \begin{pmatrix} N-K \\  n-k \end{pmatrix}} { \frac{N \left( N-1 \right)}{ n \left( n-1\right)} \begin{pmatrix} N-2 \\  n-2 \end{pmatrix}} }  + \sum _{k} { \times \frac{\begin{pmatrix} K-1 \\  k-1 \end{pmatrix} \times \begin{pmatrix} N-K \\  n-k \end{pmatrix}} {\frac{N} {n} \begin{pmatrix} N-1 \\  n-1 \end{pmatrix}} } \right)  - \left( \frac {Kn} {N} \right)^{2}\\&=\frac {K(K-1)n(n-1)} {N(N-1)} + \frac {Kn} {N} - \left( \frac {Kn} {N} \right)^{2}\\&= n \cdot \frac {K} {N} \frac {N-K} {N} \frac {N-n} {N-1} \\&& \end{align} $$

다른 방법으로는 factorial moment를 사용하여 $[E(X(X-1))]$을 구하는 방법도 있다. 수식이 조금 더 간단해진다.

따라서 흡연자이면서 폐암 환자인 사람의 수는 평균이 $\frac {Kn} {N} $, 분산이 $n \cdot \frac {K} {N} \frac {N-K} {N} \frac {N-n} {N-1} $인 정규분포를 따른다고 할 수 있다. 

정규 분포가 아닌 카이 제곱 분포를 사용하자

피어슨 경은 이 정규 분포를 바로 사용하는 것이 아니라 카이 제곱 분포를 사용하고자 했다. 이런 2*2 분할표 (contingency table)에서는 정규 분포를 쓰든 카이 제곱 분포를 쓰든 아무 상관이 없겠지만 표가 더 커지면 문제가 발생하기 마련이다.

<2*2 분할표>

<3*3 분할표>

 2*2 분할표에서는 자유도가 1이므로 한 개의 값만 지정하면 되지만, 3*3 분할표만 되어도 자유도가 4이므로 자유롭게 정할 수 있는 값이 4개가 된다. 이런 경우 정규 분포를 바로 사용할 수 없다. 따라서 정규분포를 사용하지만 자유도의 개념이 있는 카이 제곱 분포를 사용하고자 했을 것이다.

 설명을 용이하게 하기 위해 2*2 분할표로 설명을 이어가도록 하겠다. 흡연자이면서 폐암 환자인 사람의 수($X$)를 표준화한 뒤 제곱해주면 카이 제곱 분포를 따른다고 할 수 있다. 평균이 $\frac {Kn} {N} $, 분산이 $n \cdot \frac {K} {N} \frac {N-K} {N} \frac {N-n} {N-1} $이므로 

$$\frac{\left(X-\frac {Kn} {N}\right)^2}{  n \cdot \frac {K} {N} \frac {N-K} {N} \frac {N-n} {N-1} }\sim \chi^2(1) \tag{1}$$

이라고 작성할 수 있다.

 이때 $N$이 굉장히 크면 $N\sim \left(N-1\right)$이므로 $(1)$식은 $$\frac{\left(X-\frac {Kn} {N}\right)^2}{  n \cdot \frac {K \cdot (N-K) \cdot(N-n)} {N^3}}\sim \chi^2(1) \tag{2}$$

에 근사 시킬 수 있다.

수식을 정리해보자

 한편 수식$(2)$에서 쓰인 문자들은 표에서 다음과 같이 나타난다.

수식$(2)$을 어떻게 잘 정리해야 세상에 잘 먹힐지 피어슨 경은 고민이 많았을 것이다. 저 식은 너무 복잡해서 일반적인 연구자가 쓰기엔 복잡할 뿐만 아니라 쓰고 싶지 않게 생겼기 때문이다. 피어슨 경은 뛰어난 직관으로 해결했을 수도 있지만 나에게는 다음과 같이 계산되는 결과가 매력적으로 느껴졌다. 

먼저 기대 빈도를 구하면 다음과 같다.

관찰 빈도에서 기대 빈도를 뺀 뒤 제곱한 값은 놀랍게도 모든 셀에서 같다. (사실 자유도가 1이므로 당연한 현상이긴 하다.)

게다가 이 값은 수식$(2)$인 $\frac{\left(X-\frac {Kn} {N}\right)^2}{  n \cdot \frac {K \cdot (N-K) \cdot(N-n)} {N^3}}$의 분자에 해당하는 내용이다. 따라서 이 수식은 다음과 같이 바꿔보고 싶은 욕구가 차오른다.

$$ \begin{align} \frac{\left(X-\frac {Kn} {N}\right)^2}{  n \cdot \frac {K \cdot (N-K) \cdot(N-n)} {N^3}}&=\frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{Kn}{N}} \frac{\frac{Kn}{N}}{  n \cdot \frac {K \cdot (N-K) \cdot(N-n)} {N^3}}\\&= \frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{Kn}{N}} \left(  1+ \frac{N^2}{(N-K)(N-n)}-1\right)\\&= \frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{Kn}{N}} + \frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{Kn}{N}} \frac{KN+Nn-Kn}{(N-K)(N-n)}\\&=\frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{Kn}{N}} + \frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{K(N-n)}{N}} \frac{KN+Nn-Kn}{(N-K)n}\\&=\frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{Kn}{N}} + \frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{K(N-n)}{N}} \left( 1 + \frac{KN} {(N-K)n} \right)\\&=\frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{Kn}{N}} + \frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{K(N-n)}{N}}  +\frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{K(N-n)}{N}}  \frac{KN} {(N-K)n} \\&=\frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{Kn}{N}} + \frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{K(N-n)}{N}}  +\frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{(N-K)n}{N}}  \frac{N} {(N-n)} \\&= \frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{Kn}{N}} + \frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{K(N-n)}{N}}  +\frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{(N-K)n}{N}} \left( 1+  \frac{n} {(N-n)} \right)\\&=\frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{Kn}{N}} + \frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{K(N-n)}{N}}  +\frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{(N-K)n}{N}} +  \frac{\left(X-\frac {Kn} {N}\right)^2}{\frac{(N-K)(N-n)}{N}} \\&= \frac  {\left(a_{11}-e_{11}\right)^2} {e_{11}} +\frac  {\left(a_{21}-e_{21}\right)^2} {e_{21}} +\frac  {\left(a_{12}-e_{12}\right)^2} {e_{12}}+\frac  {\left(a_{22}-e_{22}\right)^2} {e_{22}} \\&= \sum_{i, j} \frac  {\left(a_{ij}-e_{ij}\right)^2} {e_{ij}} \tag{3} \\&& \end{align}$$

정리된 수식의 위엄

 이제 정확한 초기하 분포의 확률을 구하기 위해 $1000!$같은 무식한 계산을 하지 않아도 된다. $2*2$ 분할표라면 관찰 빈도와 기대 빈도로 계산한 $(3)$ 식의 값이 3.84를 넘기만 하다면 분포에 통계적으로 유의한 차이가 있다고 양측 검정 (Two-tailed or two-sided)을 한 셈이니 말이다. (3.84는 자유도가 1인 카이 제곱 분포의 누적 확률이 0.95가 되는 지점이다.) $m*n$ 분할표일 때에도 식 $(3)$과 비슷하게 계산을 먼저 하고 그 값이 카이 제곱 분포표에서 자유도 $(m-1)\times(n-1)$일 때 $\alpha=0.05$인 지점보다 큰지만 확인하면 된다.

[이론] 카이 제곱 검정과 피셔 정확 검정의 관계 정복 완료!

작성일: 2022.08.29.

최종 수정일: 2022.08.29.

[이론] 피셔 정확 검정 (Fisher's exact test)

 범주형 자료의 통계 분석을 진행하다 보면 반드시 만나게 되는 검정이 피셔 정확 검정이다. 피셔 정확 검정은 단순히 초기하 분포의 확률을 구하는 것이다. 이해할 수 있는 언어로 표현하면 다음과 같다.

초기하 분포 (Hypergeometric distritubion)

 먼저 초기하 분포를 이해해야 한다. 

상황: 10개의 공이 들어있는 주머니가 있다. 그중 7개는 파란색, 3개는 빨간색이다. 

전제: 특정 색깔의 공이 더 잘 뽑히는 것은 아니다. 어떤 색이 뽑힐지는 랜덤이다. (=뽑는 사람은 공을 보지 않고서는 색을 알 수 없다 = 독립이다.)

문제: 5개의 공을 꺼냈는데, 3개가 파란색, 2개가 빨간색일 확률은 얼마인가?

답: 

$$\frac{_{7}C_{3}\times _{3}C_{2}}{_{10}C_{5}} = \frac{\begin{pmatrix} 7 \\  3 \end{pmatrix} \times \begin{pmatrix} 3 \\  2 \end{pmatrix}} {\begin{pmatrix} 10 \\  5 \end{pmatrix}}$$

해설: 

분모에는 10개 공 중에서 5개를 고르는 경우의 수인 $_{10}C_{5}$을 넣는다.

분자에는 파란 공 7개 중 3개를 고르는 경우의 수인 $_{7}C_{3}$과 빨간 공 3개 중 2개를 고르는 $_{3}C_{2}$를 곱한다.

즉, $N$개 중 $n$개를 고르는데, 음이 아닌 어떤 정수 $k$에 대해, $k$개는 $K$중에서, $n-k$개는 $N-K$개에서 고르는 경우에 대해 논하는 것이 초기하 분포다. 그리고 확률 밀도 함수(discrete density function, 혹은 probability mass function)는 다음과 같이 기술된다.

$$f_{k} (k;K,N,n)=\frac{_{K}C_{k}\times _{N-K}C_{n-k}}{_{N}C_{n}} = \frac{\begin{pmatrix} K \\  k \end{pmatrix} \times \begin{pmatrix} N-K \\  n-k \end{pmatrix}} {\begin{pmatrix} N \\  n \end{pmatrix}}$$

 말이 어려워 보일지 몰라도 위 문제에 대한 해설을 일반화한 것뿐이다.

피셔 정확 검정 (Fisher's exact test)은 어떻게 하는 건데?

피셔 정확 검정 결과를 직접 손으로 계산해보고자 한다.

성별과 RH 혈액형 분포가 다음과 같다고 하자.

다음 두 가지를 유의하며 읽어야 한다.

1) 먼저, 카이 제곱 검정 때와 마찬가지로 합계에 있는 파란색 숫자들은 변하지 않는 고정값으로 볼 것이다.

2) 우리는 빨간색 숫자인 여성이면서 RH-인 사람의 수에 집중할 것이다.

 여성은 482명, RH-는 6명이므로 빨간색 숫자가 있는 칸에는 이론적으로 0부터 6(482와 6중 작은 숫자)까지의 숫자가 들어갈 수 있다. 만약 0이라면, RH- 6명 중 전원이 남성인 것이므로 "남성에 RH-가 많다."라고 이야기할 수도 있을 것이다. 반대로 6이라면 RH- 6명 중 전원이 여성이므로 "여성에 RH-가 많다."라고 이야기할 수도 있을 것이다.

 본 글의 최종 목적이 되는 양측 검정 (two-sided, two-tailed) 귀무가설은 "성별과 RH 혈액형은 관련성이 없다."이므로 빨간색 숫자가 있는 칸에 들어가는 숫자가 작아서 0에 가까워지거나 커서 6에 가까워지는 상황에서는 p-value가 작아지도록 통계량이 설계되어야 한다. 

 위에서 공부한 초기하 분포의 확률을 본 상황에 대입하면 다음과 같다.

전제되는 상황: 특정 성별이 특정 RH 혈액형을 가질 가능성이 더 높지 않다. 즉 독립적이다.

"총 인원 1,000명 중 RH- 6명을 고를 건데, 1명은 여성 482명 중에서, 나머지 5명은 남성 518명 중에서 고를 것이다. 그렇게 계산될 확률은 얼마인가?"

초기하 분포의 확률 공식을 사용하여 위 문제의 답은 다음과 같이 구할 수 있다.

$$ \frac{\begin{pmatrix} 482 \\  1 \end{pmatrix} \times \begin{pmatrix} 518 \\  5 \end{pmatrix}} {\begin{pmatrix} 1000 \\  6 \end{pmatrix}}=0.10739...$$

이 값이 SAS 결과에서는 "테이블 확률(P)"로 제시된다. 본 테이블이 계산될 확률을 의미한다. 

사실 피셔 정확 검정에서는 여러 대립 가설이 있을 수 있다. 각 상황에 따라 피셔 정확 검정의 결과를 계산해보고자 한다.

대립 가설 1) 여성일수록 RH-일 가능성이 높아지는 관련성이 있다.  (One-sided, One-Tailed)

 그렇다면 우리가 구하고자 하는 p-value의 의미는 다음과 같다.

"성별과 RH 혈액형 사이에는 관련성이 없다는 것이 진실인데 여성일수록 RH-일 가능성이 높아지는 관련성이 있다고 결론을 내릴 확률"

우리 데이터를 보면 RH-인 6명 중 5명이 남성에 쏠려있으므로 이 상황에서 구해지는 p-value는 높은 값을 갖는 것이 합리적이다. 그리고 그 계산은 다음 확률을 모두 더해서 계산한다.

 (1) 여성이면서 RH-인 사람이 1명일 확률 :$ \frac{\begin{pmatrix} 482 \\  1 \end{pmatrix} \times \begin{pmatrix} 518 \\  5 \end{pmatrix}} {\begin{pmatrix} 1000 \\  6 \end{pmatrix}}$

 (2) 여성이면서 RH-인 사람이 2명일 확률 :$ \frac{\begin{pmatrix} 482 \\  2 \end{pmatrix} \times \begin{pmatrix} 518 \\  4 \end{pmatrix}} {\begin{pmatrix} 1000 \\  6 \end{pmatrix}}$

 (3) 여성이면서 RH-인 사람이 3명일 확률 :$ \frac{\begin{pmatrix} 482 \\  3 \end{pmatrix} \times \begin{pmatrix} 518 \\  3 \end{pmatrix}} {\begin{pmatrix} 1000 \\  6 \end{pmatrix}}$

 (4) 여성이면서 RH-인 사람이 4명일 확률 :$ \frac{\begin{pmatrix} 482 \\  4\end{pmatrix} \times \begin{pmatrix} 518 \\  2 \end{pmatrix}} {\begin{pmatrix} 1000 \\  6 \end{pmatrix}}$

 (5) 여성이면서 RH-인 사람이 5명일 확률 :$ \frac{\begin{pmatrix} 482 \\  5 \end{pmatrix} \times \begin{pmatrix} 518 \\  1 \end{pmatrix}} {\begin{pmatrix} 1000 \\  6 \end{pmatrix}}$

 (6) 여성이면서 RH-인 사람이 6명일 확률 :$ \frac{\begin{pmatrix} 482 \\  6 \end{pmatrix} \times \begin{pmatrix} 518 \\  0 \end{pmatrix}} {\begin{pmatrix} 1000 \\  6 \end{pmatrix}}$

이 값을 모두 더하면, 즉 $$\sum_{k=1}^{6} { \frac{\begin{pmatrix} 482 \\  k \end{pmatrix} \times \begin{pmatrix} 518 \\  6-k \end{pmatrix}} {\begin{pmatrix} 1000 \\  6 \end{pmatrix}}}=0.98085...$$

가 되어 SAS 결과에서의 "상단측 p값 Pr>=F"값이 산출된다. 

(1) 여성이면서 RH-인 사람의 수는 1이다. 이를 F라 칭한다.

(2) 여성이면서 RH-인 사람의 수가 F 이상인 확률들의 총합을 "상단측 p값 Pr>=F"라고 한다.

만약 유의성의 기준 ($\alpha$)이 0.3였다면 다음과 같이 해석된다.

성별과 RH혈액형 사이에 관련성이 없다는 것이 진실이라고 가정하자. 이때 RH- 환자 6명 중 한 명 이상이 여성일 확률은 0.9810다. 이건 0.3보다도 높으므로 현실적으로 일어날 수 있는 일이다. 따라서 여성일수록 RH- 혈액형을 가질 것이라고는 할 수 없다고 결론지어진다.

대립 가설 2) 여성일수록 RH-일 가능성이 낮아지는 관련성이 있다.  (One-sided, One-Tailed)

 그렇다면 우리가 구하고자 하는 p-value의 의미는 다음과 같다.

"성별과 RH 혈액형 사이에는 관련성이 없다는 것이 진실인데 여성일수록 RH-일 가능성이 낮아지는 관련성이 있다고 결론을 내릴 확률"

우리 데이터를 보면 RH-인 6명 중 1명만이 여성이므로 이 상황에서 구해지는 p-value는 상대적으로 낮은 값을 갖는 것이 합리적이다. 그리고 그 계산은 다음 확률을 모두 더해서 계산한다.

 (1) 여성이면서 RH-인 사람이 0명일 확률 :$ \frac{\begin{pmatrix} 482 \\  0 \end{pmatrix} \times \begin{pmatrix} 518 \\  6 \end{pmatrix}} {\begin{pmatrix} 1000 \\  6 \end{pmatrix}}$

 (2) 여성이면서 RH-인 사람이 1명일 확률 :$ \frac{\begin{pmatrix} 482 \\  1 \end{pmatrix} \times \begin{pmatrix} 518 \\  5 \end{pmatrix}} {\begin{pmatrix} 1000 \\  6 \end{pmatrix}}$

이 값을 모두 더하면, 즉 $$\sum_{k=0}^{1} { \frac{\begin{pmatrix} 482 \\  k \end{pmatrix} \times \begin{pmatrix} 518 \\  6-k \end{pmatrix}} {\begin{pmatrix} 1000 \\  6 \end{pmatrix}}}=0.12644...$$

가 되어 SAS 결과에서의 "하단측 p값 Pr>=F"값이 산출된다.

(1) 여성이면서 RH-인 사람의 수는 1이다. 이를 F라 칭한다.

(2) 여성이면서 RH-인 사람의 수가 F 이하인 확률들의 총합을 "하단측 p값 Pr<=F"라고 한다.

만약 유의성의 기준 ($\alpha$)이 0.3였다면 다음과 같이 해석된다.

성별과 RH혈액형 사이에 관련성이 없다는 것이 진실이라고 가정하자. 이때 RH- 환자 6명 중 한 명 이하만이 여성일 확률은 0.1264다. 이 값은 0.3보다도 낮으므로 이렇게 적은 숫자의 여성이 RH-혈액형을 갖는 것은 현실적으로 일어나기 어려운 일이다. 그러므로 성별과 RH혈액형 사이에 관련성이 없다고 봤던 가정에 문제가 있다고 할 수 있다. 따라서 차라리 여성일수록 RH-혈액형일 가능성이 떨어진다고 보는 것이 합리적이다. 

즉 사고의 흐름은 다음과 같다.

"RH-인 사람 중 여성이 1명밖에 안되네?"

$\rightarrow$ "1명 혹은 0명 밖에 없다는 것은 여성일수록 RH-일 가능성이 떨어진다는 것 아닐까?"

$\rightarrow$  [가정] "성별이랑 RH혈액형 간에 아무런 관계가 없다고 가정해보자."

$\rightarrow$ "그때 RH-중 1명 혹은 0명만이 여성일 확률이 얼마라고? 0.1264라고."

$\rightarrow$ "이게 현실적으로 일어나기는 어려운 일 아니야?"

$\rightarrow$ "그러면 차라리 여성일수록 RH-일 확률이 높은 게 진실이고 그런 현실 속에서 발생한 일이라고 보는 게 낫겠다."

대립 가설 3) 성별과 RH 혈액형 사이에는 모종의 관련성이 있다.  (Two-sided, Two-Tailed)

 그렇다면 우리가 구하고자 하는 p-value의 의미는 다음과 같다.

"성별과 RH 혈액형 사이에는 관련성이 없다는 것이 진실인데 여성일수록 RH-일 가능성이 높아지거나 낮아지는 관련성이 있다고 결론을 내릴 확률"

 모종의 관련성이 있다면 여성이면서 RH-인 사람의 수는 극도로 작아지거나 커질 것이다. 여기에서는 그 수가 1이다. 1이 될 확률은 위에서 0.1074로 산출이 되었다. 그 확률보다 작은 경우는 여성이면서 RH-인 사람의 수가 1보다 적거나, 6에 가까운 경우일 뿐일 것이다. 그 확률들의 총합이 피셔 정확 검정의 양측 검정 p-value이다. 

Yes에 해당하는 사람들의 확률을 모두 더하면 $0.21917$이 계산되며 이는 SAS 결과에서의 "양측 p값 Pr>=P"와 같다. 또한, 이 값이 보통 논문에서 사용되는 피셔 정확 검정의 값이다.

만약 유의성의 기준 ($\alpha$)이 0.3였다면 다음과 같이 해석된다.

성별과 RH혈액형 사이에 관련성이 없다는 것이 진실이라고 가정하자. 이때 RH- 환자 6명 중 한 명만이 여성일 확률은 0.1074다. 이 확률보다 일어나기 어려운 현상은 RH-인 여성이 0명인 상황, 5명인 상황, 6명인 상황이다. 이런 일들이 일어날 확률은 0.2192다. 이건 0.3보다도 낮으므로 현실적으로 일어나기 어렵다. 즉, 성별과 RH혈액형 사이에 관련성이 없다고 봤던 가정에 문제가 있다고 할 수 있다. 따라서 차라리 여성일수록 RH-혈액형일 가능성이 높아지거나 낮아지는 것이 진실이라고 보는 것이 합리적이다. 

세 가지 p-value 중 어떤 값을 써야 하는가?

피셔 정확 검정의 p-value는 아무 거나 쓰는 것이 아니다. 어떤 대립 가설을 사용하는지에 따라 크게 달라진다.

1) 상단측 p값 Pr>=F : 분할표의 대각선에 많은 데이터가 몰릴 것으로 예상될 때 사용한다. 만약 변수가 순서형 변수라면 크기순으로 행과 열을 채우니 일반적으로 양의 상관관계가 예상될 때 사용한다고 할 수 있다.

2) 하단측 p값 Pr<=F : 분할표의 대각선에 외의 셀에 많은 데이터가 몰릴 것으로 예상될 때 사용한다. 만약 변수가 순서형 변수라면 크기순으로 행과 열을 채우니 일반적으로 음의 상관관계가 예상될 때 사용한다고 할 수 있다.

3) 양측 p값 Pr<=P : 대립 가설이 없을 때 사용한다. 즉, 어느 방향으로든 관련성이 있는지 보고자 할 때 사용하는 값이다.

[이론] 피셔 정확 검정 (Fisher's exact test) 정복 완료!

작성일: 2022.08.26.

최종 수정일: 2022.08.27.

이용 프로그램: SAS v9.4

운영체제: Windows 10

[SAS] 카이 제곱 검정 - PROC FREQ

 카이 제곱 검정은 범주형 변수 간에 분포의 유의미한 차이가 있는지 확인하는 방법이다. 이해할 수 있는 언어로 표현하면 다음과 같다. 분할표를 작성하였을 때 다음과 같다고 하자. (출처 및 분할표 작성법:2022.08.18 - [기술 통계/SAS] - [SAS] 도수분포표 (Frequency table), 분할표 (Contingency table) 만들기 - PROC FREQ)

이를 보면 비음주자 중에는 여성이 많고, 음주자 중에는 남성이 많다. 그렇다면 "성별과 음주 여부는 무관하다(=독립이다)."라는 말이 틀리다고 할 수 있을까? 즉, "특정 성별은 음주자일 확률이 더 높다."라고 할 수 있을까? 이에 대한 검정이 바로 카이 제곱 검정이다.

*실습용 데이터는 아래 링크를 클릭하면 다운로드할 수 있습니다.

2022.08.04 - [공지사항 및 소개] - 분석용 데이터 (update 22.08.18)

시작하기 위해 라이브러리를 만들고, 파일을 불러온다.

라이브러리 만드는 방법: 2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 라이브러리 만들기 - LIBNAME

파일 불러오는 방법: 2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 데이터 불러오기 및 저장하기 - PROC IMPORT, PROC EXPORT

*라이브러리 지정하기;
LIBNAME hong "C:/Users/User/Documents/Tistory_blog";

*파일 불러오기;
PROC IMPORT
DATAFILE="C:\Users\user\Documents\Tistory_blog\Data.xlsx"
DBMS=EXCEL
OUT=hong.df
REPLACE;
RUN;

코드

카이 제곱 검정을 시행하는 코드는 다음과 같다.

PROC FREQ DATA=hong.df;
TABLE SEX*ALCOHOL/CHISQ;
RUN;

PROC FREQ DATA=hong.df; : 빈도수를 계산하는 코드를 시작하며, 데이터는 hong 라이브러리의 df 파일을 이용한다.
TABLE SEX*ALCOHOL/CHISQ; : SEX와 ALCOHOL의 분할표를  계산하며, 카이 제곱 검정을 시행한다.

분할표를 작성하는 코드와 거의 똑같고, TABLE 구문에 옵션으로  "CHISQ"가 추가된 것만이 다르다.

결과

 많은 값들이 산출되지만 봐야 할 것은 카이제곱 검정량이다. 카이 제곱 검정량은 24.3892이며, 자유도가 1인 카이제곱 분포에서 이런 일이 발생할 확률은 0.0001 미만이다. 따라서 유의성 기준을 0.05로 잡았을 때, 성별과 음주 여부는 독립이 아니라고 할 수 있으며, 남성이 음주할 확률이 더 높다고 할 수 있다.

 이 해석을 할 때에, 빈도, 백분율, 행 백분율, 칼럼 백분율은 사실 필요가 없다. 따라서 이 지표들을 산출하지 않기 위해 옵션으로 TABLE구문에 NOFREQ NOPERCENT NOROW NOCOL를 추가하기도 한다. 또한, 카이 제곱 검정을 시행하기 위한 전제조건은 기대 빈도가 5 미만이 셀이 전체 셀 중 25% 미만이어야 한다는 것이므로 기대 빈도를 확인해볼 수 있는 옵션인 EXPECTED를 추가하기도 한다. 

코드

PROC FREQ DATA=hong.df;
TABLE SEX*ALCOHOL/CHISQ NOFREQ NOPERCENT NOROW NOCOL EXPECTED;
RUN;

결과

기대 빈도는 197.62, 284.38, 212.38, 305.62로 모두 5보다 크므로 카이 제곱 검정을 시행하는데 문제가 없다.

SAS 카이 제곱 검정 정복 완료!

작성일: 2022.08.19.

최종 수정일: 2022.08.19.

이용 프로그램: SAS v9.4

운영체제: Windows 10