의학 통계 코드 저장소

[SPSS] 등분산 가정이 성립하지 않는 일원 배치 분산 분석 (Welch's ANOVA, Brown-Forsythe ANOVA) 

이전 포스팅에서 흡연 상태를 "1) 비흡연자", "2) 과거 흡연자", "3) 현재 흡연자"로 나누었고, 각 그룹의 폐기능 검사 중 하나인 FVC (Forced Vital Capacity)의 평균에 차이가 있는지 알아보고자 하여 일원 배치 분산 분석 (ANOVA)를 시행하였다. 2022.11.30 - [모평균 검정/SPSS] - [SPSS] 일원 배치 분산 분석 (One-way ANOVA, ANalysis Of VAriance)

ANOVA의 전제 조건은 두 가지였다.

1) 정규성

2) 등분산성

만약 '1) 정규성'은 만족하지만 '2) 등분산성'이 성립하지 않는 경우에는 어떻게 해야 할까?

당연히, 이전 포스팅의 일반적인 ANOVA는 실시할 수 없고, Welch's ANOVA 혹은 Brown-Forsythe ANOVA를 시행해야 한다.

 - 이 Brown-Forsythe ANOVA는 Brown-Forsythe의 등분산성 검정과는 다른 것이다. (아래에서 설명함)

이번 포스팅에서는 이 Welch's ANOVA와 Brown-Forsythe ANOVA를 다뤄보고자 한다.

*실습용 데이터는 아래 링크를 클릭하면 다운로드할 수 있습니다.

2022.08.04 - [공지사항 및 소개] - 분석용 데이터 (update 22.11.28)

데이터를 불러오도록 한다. 불러오는 방법은 다음 링크를 확인하도록 한다.

2022.08.04 - [통계 프로그램 사용 방법/SPSS] - [SPSS] 데이터 불러오기 및 저장하기

목표:  거주 지역 단위에 따라 삶의 질의 평균이 모집단 수준에서 서로 다르다고 말할 수 있는가?

전제조건 (정규성)

 Welch's ANOVA 및 Brown-Forsythe ANOVA에는 하나의 전제조건이 필요하다. 본 포스팅의 예시에 맞추어 설명하면 다음과 같다.

  - 정규성: 대도시, 중소도시, 시골 거주자 별로 삶의 질의 분포를 보았을 때 각각의 분포는 정규성을 따른다. 

그리고, 분산은 같지 않아도 된다.

2022.08.11 - [기술 통계/SPSS] - [SPSS] 정규성 검정

2022.08.18 - [기술 통계/SPSS] - [SPSS] 고급 Q-Q Plot - Van der Waerden, Rankit, Tukey, Blom

1) 정규성

1) 분석(A) > 기술통계량(E) > 데이터 탐색 (E)

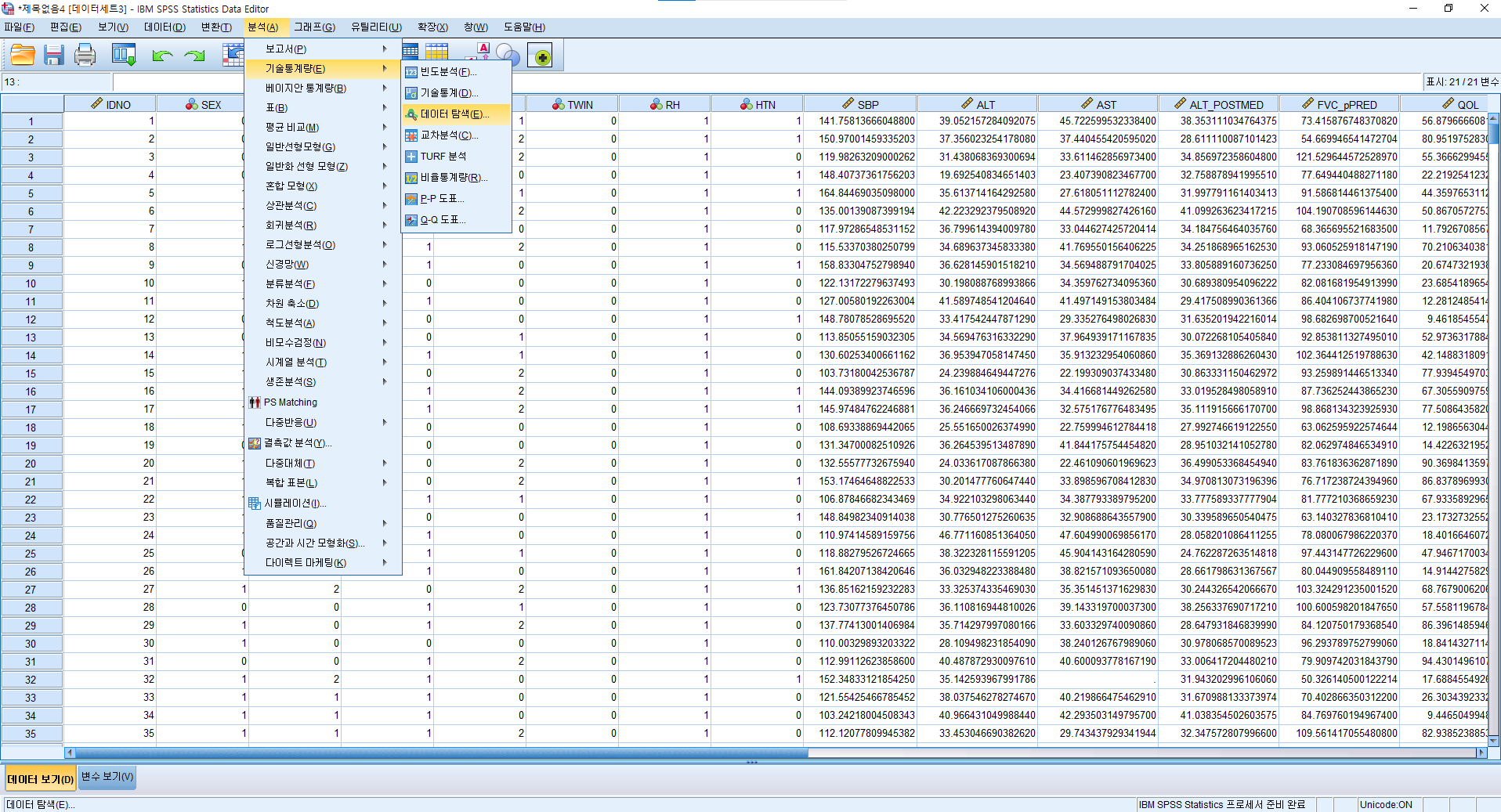
2) 분석하고자 하는 변수인 QOL을 "종속변수"에 넣어준다. 거주 지역 단위에 따라 정규성을 검정할 것이므로 "요인(F)"에 RESID를 넣는다. 그 뒤 "도표(T)..."를 선택한다.

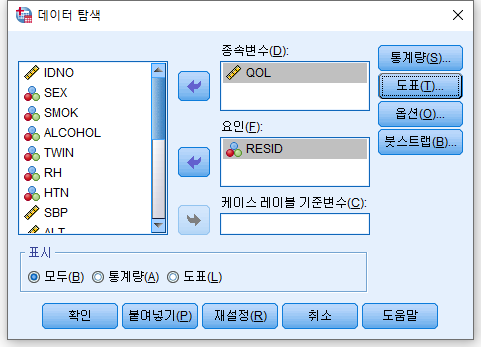
3) "히스토그램(H)", "검정과 함께 정규성 도표(O)" 체크박스를 클릭하고 "계속(C)"를 누르고, 돌아가 "확인"을 누른다.

결과

1) Q-Q plot

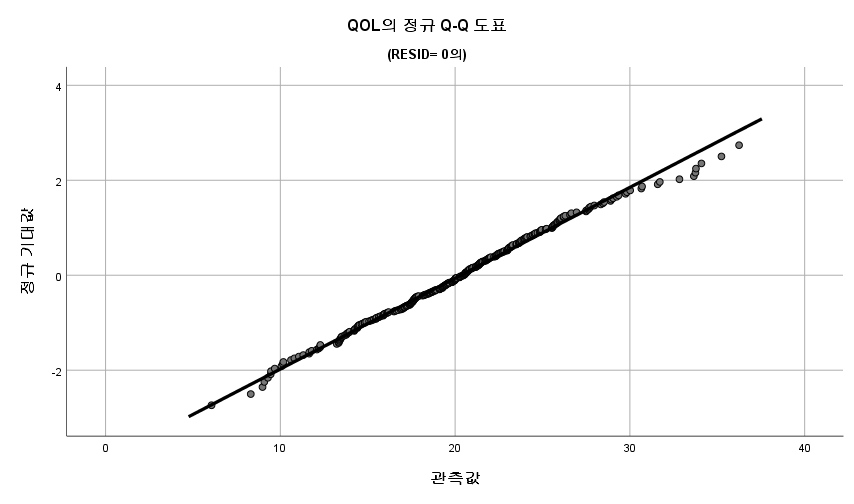
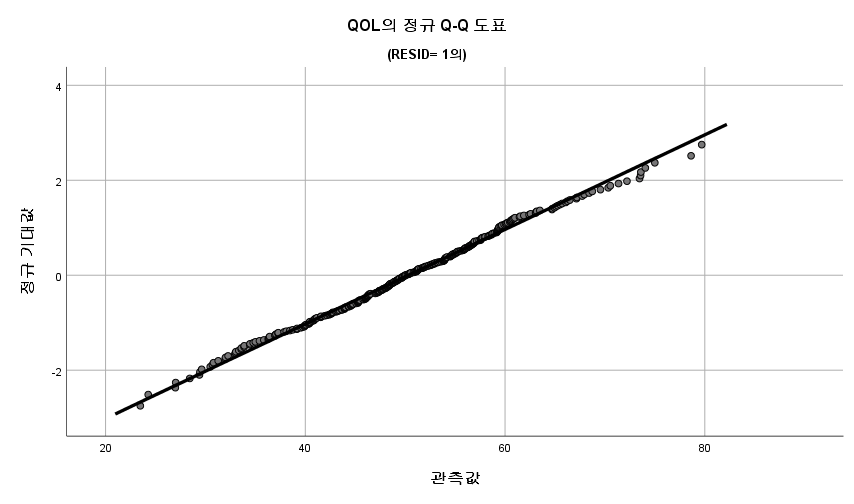
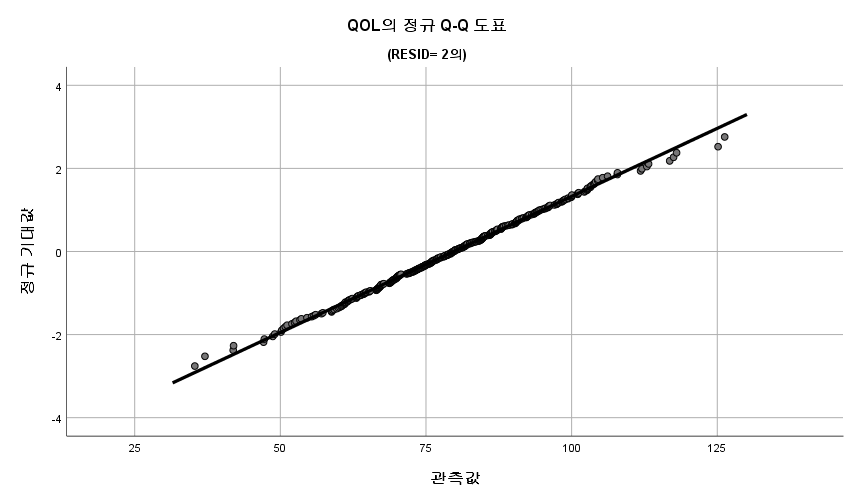
2) 히스토그램

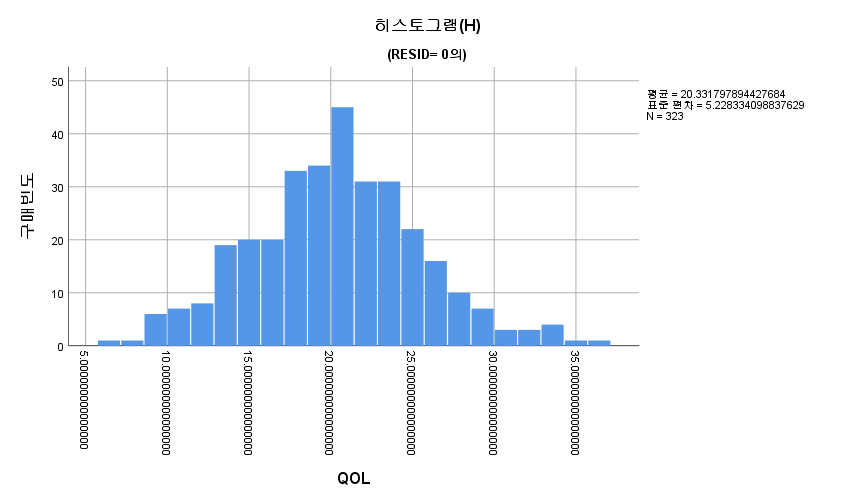
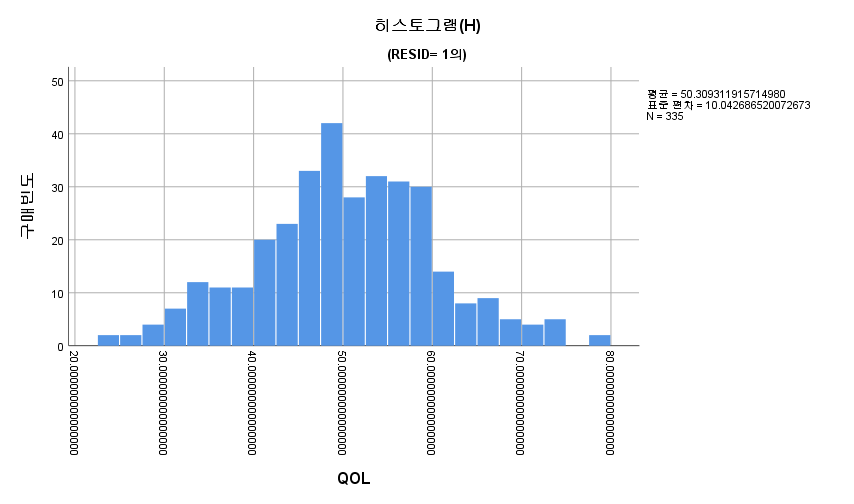
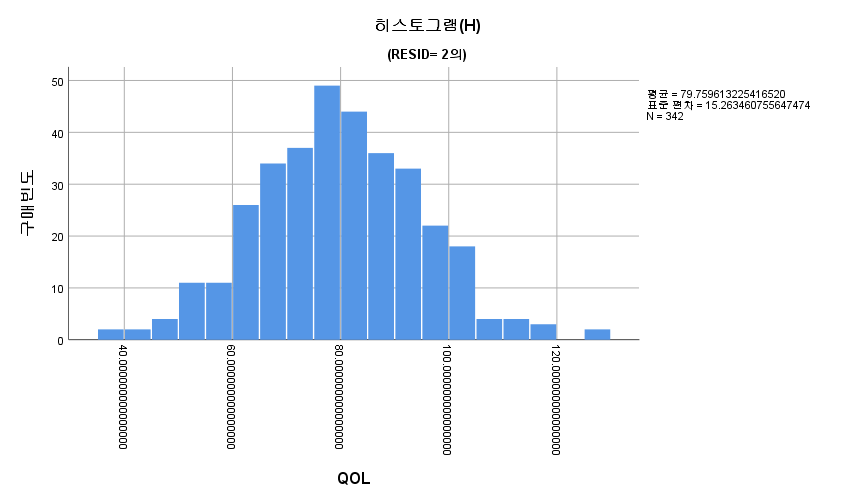
3) Shapiro-Wilk 검정

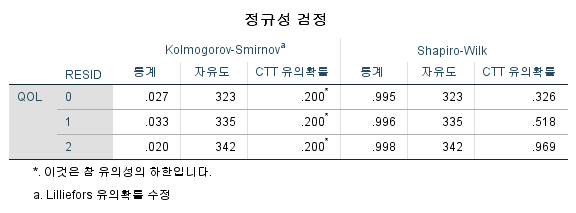
표본의 수가 2,000이 되지 않으므로 Shapiro-Wilk 통계량의 p-value를 보아야 하고, 이는 0.05보다 크다. Q-Q plot, 히스토그램에서 정규성을 띠지 않는다고 할만한 근거가 없으므로 정규성을 따른다고 결론을 짓는다.

따라서 정규성 전제는 따른다고 할 수 있다.

Welch's & Brown-Forsythe ANOVA 실행 방법

1) 분석(A) > 평균 비교 (M) > 일원배치 분산분석(O)

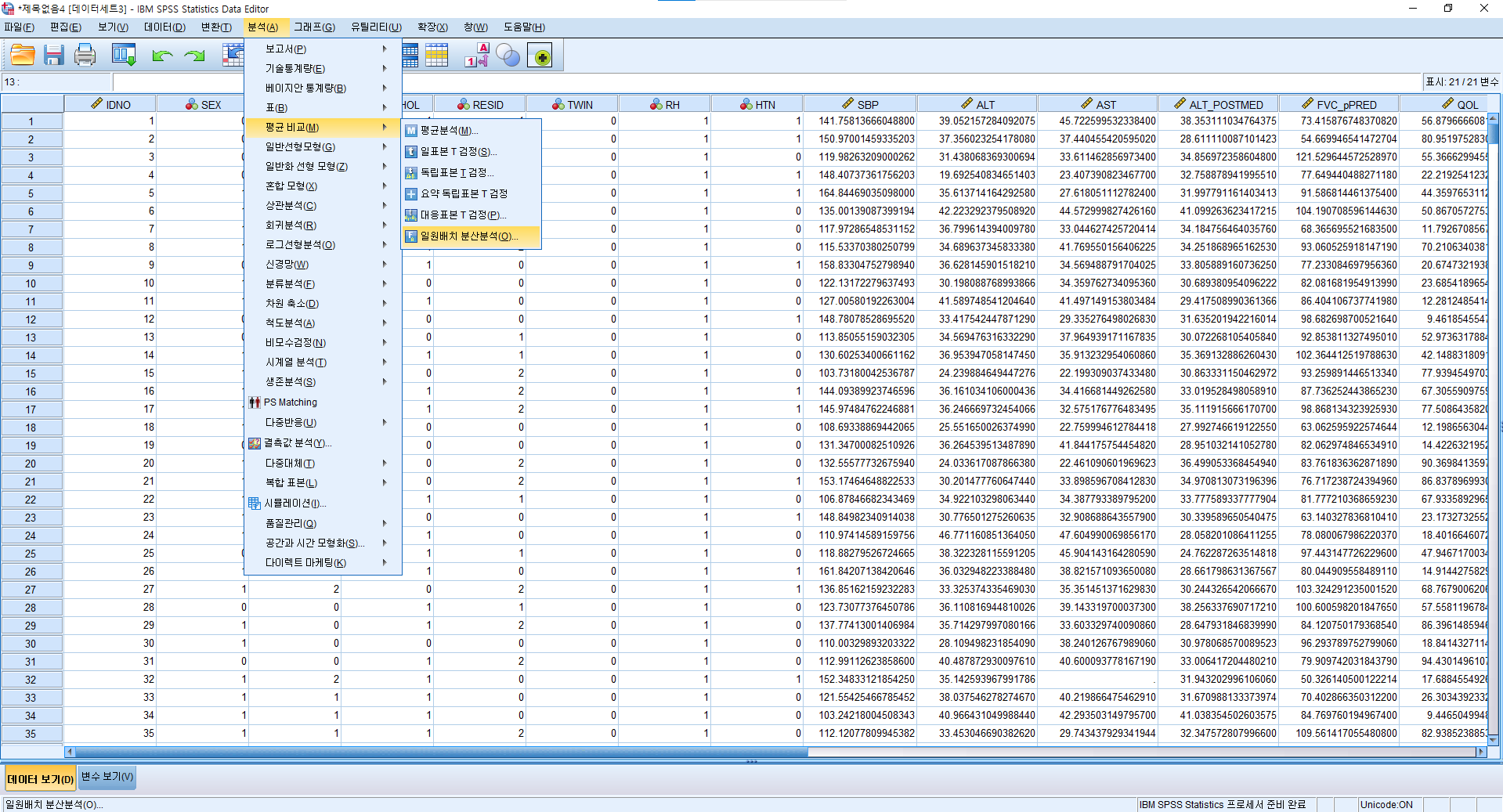
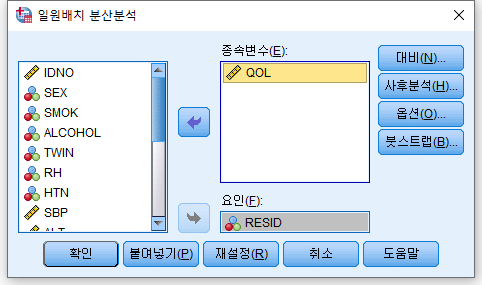
2) 분석하고자 하는 변수 QOL를 "종속변수(E)"쪽으로 옮기고, RESID을 "요인(F)"쪽으로 옮긴다. 그리고 "옵션"을 누른다.

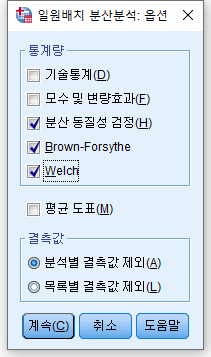
3) "분산 동질성 검정(H)" 체크박스를 선택한다. 분산이 같지 않을 경우를 대비해 "Brown-Forsythe", "Welch" 체크박스를 클릭한다.  그리고 "계속 (C)"을 누른다.

4)  "사후분석(H)"을 클릭한다.

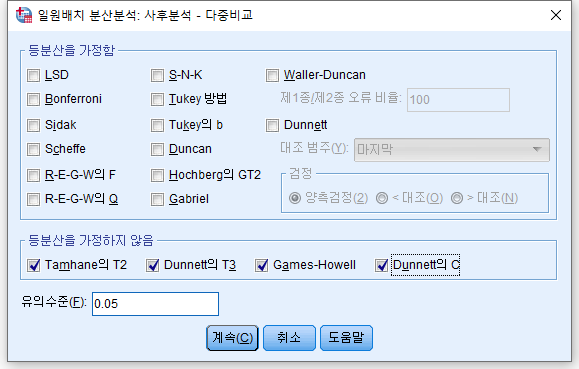
분산이 같지 않을 경우에만 대비하여 "Tanhame의 T2", "Dunnett의 T3", "Games-Howell", "Dunnett의 C"를 클릭한다. 분산이 같지 않은 경우 위쪽에 있는 사후 분석 방법은 사용할 수 없고 아래 사후 분석만 사용할 수 있다.

결과

 1) 등분산성 검정

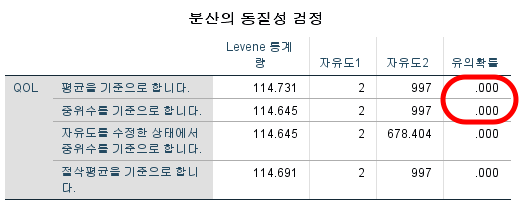
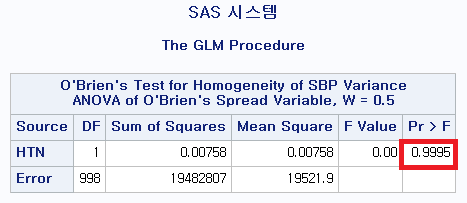
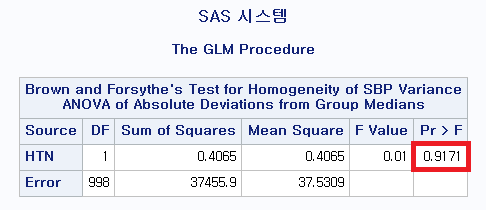
맨 위에 평균을 기준으로 한 검정이 일반적인 Levene의 등분산 검정이다.

그다음 중위수를 기준으로 한 검정이 Brown-Forsythe의 등분산성 검정이다.

어떤 것을 선택하는지는 개인의 선택이다. 하지만 이 경우 둘 다 0.05보다 작으므로 귀무가설을 기각하고, 분산에 차이가 있다고 결론 내린다.

2) 일반 ANOVA

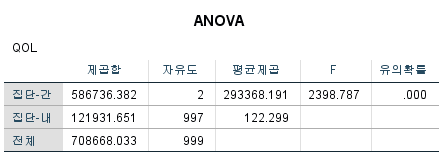
분산이 다르다고 결론 내렸으므로 이 표는 보면 안 된다.

3) Welch, Brown-Forsythe ANOVA

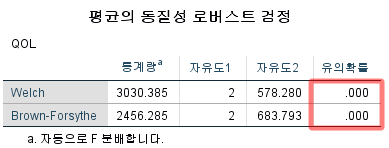
두 가지 방법 모두 p-value가 0.001보다 작다고 이야기하고 있다. 따라서 귀무가설을 기각하고 대립 가설을 채택한다. 그렇다면 여기에서 귀무가설 및 대립 가설은 무엇이었는가?

 귀무가설:  $H_0 =$세 집단의 모평균은 "모두" 동일하다.

 대립 가설:  $H_1 =$세 집단의 모평균이 모두 동일한 것은 아니다.

우리는 대립 가설을 채택해야 하므로 "세 집단의 모평균이 모두 동일한 것은 아니다."라고 결론 내릴 것이다.

그런데, 세 집단의 모평균이 모두 동일하지 않다는 말은 세 집단 중 두 개씩 골라 비교했을 때, 적어도 한 쌍에서는 차이가 난다는 것이다. 따라서 세 집단 중 두 개씩 골라 비교를 해보아야 하며, 이를 사후 분석 (post hoc analysis)이라고 한다. 세 집단에서 두 개씩 고르므로 가능한 경우의 수는$_3C_2=3$이다. 

 (1) 대도시 거주자 vs 중소도시 거주자

 (2) 대도시 거주자 vs 시골 거주자

 (3) 중소도시 거주자 vs 시골 거주자

사후 분석 결과를 볼 것이다.

이전 일반 ANOVA 포스팅(2022.11.30 - [모평균 검정/SPSS] - [SPSS] 일원 배치 분산 분석 (One-way ANOVA, ANalysis Of VAriance))에서는 여러 사후 분석 방법이 있다고 소개했었다. 하지만 등분산이 가정되지 않는 상황에서 쓸 수 있는 사후 분석 방법은 현저히 적어진다. 많이들 쓰는 방법은 다음 네 가지다.

1) Tamhane's T2

2) Games-Howell

3) Dunnett's T3

4) Dunnett's C

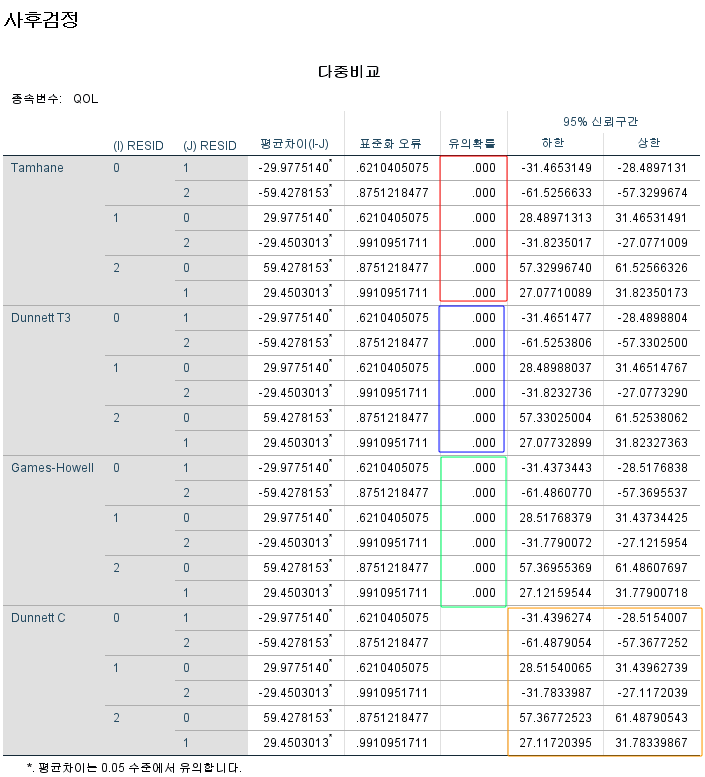
1) Tamhane's T2

2) Games-Howell

3) Dunnett's T3

4) Dunnett's C

박스 색깔과 검정방법을 매칭 시켜두었다.

위 표를 보는 법은 다음과 같다.

Dunnett C를 제외하고, 어떤 방법을 사용하든, 모든 비교에서 p-value는 0.001보다 작아 매우 유의하다. 그리고 Dunnett C는 신뢰구간에 0이 포함되지 않으면 유의한 것인데, 0을 포함하는 구간이 없다. 따라서 모든 비교에서 유의미한 FVC의 차이가 있다고 할 수 있다.

어떤 사후 분석을 쓸 것인가

 이 논의에 대해 정답이 따로 있는 것은 아니다. 적절한 방법을 사용하여 논문에 제시하면 되고, 어떤 것이 정답이라고 콕 집어 이야기할 수는 없다. 다만, 사후 분석 방법이 여러 가지가 있다는 것은 '사후 분석 방법에 따라 산출되는 결과가 달라질 수 있다.'는 것을 의미하고, 심지어는 '어떤 사후 분석 방법을 채택하냐에 따라 유의성 여부가 달라질 수도 있다.'는 것을 의미한다. 심지어, Welch's or Brown-Forsythe's ANOVA에서는 유의한 결과가 나왔는데, 사후 분석을 해보니 유의한 차이를 보이는 경우가 없을 수도 있다. 따라서 어떤 사후 분석 방법 결과에 따른 결과인지 유의하여 해석할 필요가 있다.

[SPSS] 등분산 가정이 성립하지 않는 일원 배치 분산 분석 (Welch's ANOVA, Brown-Forsythe ANOVA) 정복 완료

작성일: 2022.11.30.

최종 수정일: 2022.11.30.

이용 프로그램: IBM SPSS v26

운영체제: Windows 10

[R] 등분산성 검정 (Homogeneity of variance) - levene.test(), bartlett.test()

 T-test, ANOVA 등 몇몇 분석에서는 분포들의 분산이 같다는 가정 (등분산성)이 필요하다. 이럴 때에는 등분산성 검정을 해야 하는데, 많이들 사용하는 방법은 크게 다섯 가지가 존재한다.

1) F test

2) Levene의 등분산 검정

3) O'Brien의 등분산 검정(R에서 검정 불가)

4) Brown and Forsythe의 등분산 검정

5) Bartlett의 등분산 검정

이 중 F test, Levene의 등분산성 검정은 T-test에 관한 글에서 다루었으므로 본 포스팅에서는 다루지 않겠다. Fooled F와 Levene 등분산성 검정에 관한 내용은 다음 링크에서 확인할 수 있다. 2022.11.12 - [모평균 검정/R] - [R] 독립 표본 T검정 (Independent samples T-test) - t.test(), var.test(), levene.test()

 결국 우리가 확인하고자 하는 것은, "수축기 혈압 분포의 분산이 고혈압 환자군과 일반인 사이에서 다르다고 할 수 있는가?"이다. 이에 대해 설면하도록 하겠다.

*실습용 데이터는 아래 링크를 클릭하면 다운로드할 수 있습니다.

2022.08.04 - [공지사항 및 소개] - 분석용 데이터 (update 22.10.11)

코드를 보여드리기에 앞서 워킹 디렉토리부터 지정하겠다.

워킹 디렉토리에 관한 설명은 다음 링크된 포스트에서 볼 수 있다.

2022.08.05 - [통계 프로그램 사용 방법/R] - [R] 작업 디렉토리 (Working Directory) 지정 - getwd(), setwd()

setwd("C:/Users/user/Documents/Tistory_blog")

데이터를 불러와 df에 객체로 저장하겠다.

데이터 불러오는 방법은 다음 링크에서 볼 수 있다.

2022.08.05 - [통계 프로그램 사용 방법/R] - [R] 데이터 불러오기 : EXCEL - read_excel(), read.xlsx()

2022.08.10 - [통계 프로그램 사용 방법/R] - [R] 데이터 저장하기 : CSV 파일 - write.csv(), write_csv()

2022.08.10 - [통계 프로그램 사용 방법/R] - [R] 데이터 불러오기 : SAS file (.sas7bdat) - read.sas7bdat(), read_sas()

install.packages("readr")
library("readr")
df<-read_csv("Data.csv")

코드 - 등분산성 검정

Brown&Forsythe 의 등분산 검정은 "levene.test()"라는 함수를 쓰는데, 이는 "lawstat"이라는 패키지에 있으므로 설치를 한다. Bartlett의 등분산 검정을 시행할 때 사용하는 "bartlett.test()"는 기본 내장 함수이므로 별도의 설치가 필요 없다.

설치에 관한 내용은 다음 링크에서 확인할 수 있다. 2022.08.05 - [통계 프로그램 사용 방법/R] - [R] 패키지 설치하기 - install.packages(), library()

install.packages("lawstat")
library("lawstat")

등분산성을 검정하는 코드는 다음과 같다.

#Brown&Forsythe
levene.test(df$SBP, df$HTN)

#Bartlett
bartlett.test(df$SBP, df$HTN)

#Brown&Forsythe
levene.test(df$SBP, df$HTN) : df 데이터의 SBP(수축기 혈압) 변수를 df 데이터의 HTN(고혈압 여부) 변수에 따라 Brown&Forsythe 등분산 검정을 시행하라.

#Bartlett
bartlett.test(df$SBP, df$HTN) : df 데이터의 SBP(수축기 혈압) 변수를 df 데이터의 HTN(고혈압 여부) 변수에 따라 Bartlett 등분산 검정을 시행하라.

결과 

	Modified robust Brown-Forsythe Levene-type test based on
	the absolute deviations from the median

data:  df$SBP
Test Statistic = 0.010831, p-value = 0.9171

	Bartlett test of homogeneity of variances

data:  df$SBP and df$HTN
Bartlett's K-squared = 3.5705e-07, df = 1, p-value =0.9995

Modified robust Brown-Forsythe Levene-type test based on
the absolute deviations from the median

data:  df$SBP
Test Statistic = 0.010831, p-value = 0.9171

Bartlett test of homogeneity of variances

data:  df$SBP and df$HTN
Bartlett's K-squared = 3.5705e-07, df = 1, p-value =0.9995

결과가 복잡해 보이지만 위에 색깔 처리해놓은 숫자만 봐도 충분하다.

Brown-Forsythe 검사 결과 p-value는 0.9171이고

Bartlett test 검사 결과 p-value는 0.9995이다.

즉 어떤 방법을 사용하더라도, 모두 p-value가 0.05 이상으로 귀무가설을 기각하지 못해 모분산이 서로 같다고 결론 내릴 수 있다. 

코드 정리

#워킹 디렉토리 지정
setwd("C:/Users/user/Documents/Tistory_blog")

#데이터 불러오기
install.packages("readr")
library("readr")
df<-read_csv("Data.csv")

#levene.test() 함수를 위한 패키지 설치
install.packages("lawstat")
library("lawstat")

#Brown&Forsythe 등분산 검정
levene.test(df$SBP, df$HTN)

#Bartlett 등분산 검정
bartlett.test(df$SBP, df$HTN)

[R] 등분산성 검정 (Homogeneity of variance: Brown&Forsythe, Bartlett test) 정복 완료!

작성일: 2022.11.20.

최종 수정일: 2022.11.20.

이용 프로그램: R 4.2.2

RStudio v2022.07.2

RStudio 2022.07.2+576 "Spotted Wakerobin" Release

운영체제: Windows 10, Mac OS 12.6.1

[SAS] 등분산성 검정 (Homogeneity of variance) - PROC GLM

 T-test, ANOVA 등 몇몇 분석에서는 분포들의 분산이 같다는 가정 (등분산성)이 필요하다. 이럴 때에는 등분산성 검정을 해야 하는데, 많이들 사용하는 방법은 크게 다섯 가지가 존재한다.

1) Fooled F

2) Levene

3) O'Brien

4) Brown and Forsythe

5) Bartlett

이 중 첫 번째 방법인 Fooled F 검정은 PROC TTEST에서 확인할 수 있다. 그리고 Levene의 등분산성 검정은 T-test에 관한 글에서 다루었으므로 본 포스팅에서는 다루지 않겠다. Fooled F와 Levene 등분산성 검정에 관한 내용은 다음 링크에서 확인할 수 있다. 2022.10.04 - [모평균 검정/SAS] - [SAS] 독립 표본 T검정 (Independent samples T-test) - PROC TTEST

 결국 우리가 확인하고자 하는 것은, "수축기 혈압 분포의 분산이 고혈압 환자군과 일반인 사이에서 다르다고 할 수 있는가?"이다. 이에 대해 설면하도록 하겠다.

*실습용 데이터는 아래 링크를 클릭하면 다운로드할 수 있습니다.

2022.08.04 - [공지사항 및 소개] - 분석용 데이터 (update 22.08.29)

시작하기 위해 라이브러리를 만들고, 파일을 불러온다.

라이브러리 만드는 방법: 2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 라이브러리 만들기 - LIBNAME

파일 불러오는 방법: 2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 데이터 불러오기 및 저장하기 - PROC IMPORT, PROC EXPORT

*라이브러리 지정하기;
LIBNAME hong "C:/Users/User/Documents/Tistory_blog";

*파일 불러오기;
PROC IMPORT
DATAFILE="C:\Users\user\Documents\Tistory_blog\Data.xlsx"
DBMS=EXCEL
OUT=hong.df
REPLACE;
RUN;

코드 - 등분산성 검정

등분산성을 검정하는 코드는 다음과 같다.

*O'Brien;
PROC GLM DATA=hong.df;
   CLASS HTN;
   MODEL SBP = HTN;
   MEANS HTN / HOVTEST=OBRIEN(W=0.5);
RUN;
QUIT;

*Brown and Forsythe;
PROC GLM DATA=hong.df;
   CLASS HTN;
   MODEL SBP = HTN;
   MEANS HTN / HOVTEST=BF;
RUN;
QUIT;

*Bartlett;
PROC GLM DATA=hong.df;
   CLASS HTN;
   MODEL SBP = HTN;
   MEANS HTN / HOVTEST=BARTLETT;
RUN;
QUIT;

PROC GLM DATA=hong.df; : 등분산 검정은 PROC GLM이라는 명령문으로 할 수 있다. PROC GLM을 시행하고, 데이터는 hong 라이브러리에 있는 df를 이용한다.
   CLASS HTN; : 고혈압 여부(HTN)에 따라 분산이 같은지 검정할 것이다.
   MODEL SBP = HTN; : 고혈압 여부(HTN)에 따라 수축기 혈압(SBP)의 분산이 같은지 검정할 것이다.
   MEANS HTN / HOVTEST=OBRIEN(W=0.5); : 고혈압의 평균을 구해주어라. 등분산성 검정 (HOmogeneity of Variance TEST)은 O'Brien방법을 사용한다. O'Brien 방법의 parameter는 W가 있는데 원하는 값을 넣어주면 된다. 기본 값은 0.5로 설정되어 있으며, 기본값 그대로 사용하고자 할 때에는 "(W=0.5)"를 통째로 쓰지 않아도 괜찮다.
RUN; : 코드를 실행한다.
QUIT; : GLM코드는 QUIT구문을 실행하거나, 다른 코드를 실행해야만 끝나므로 QUIT을 실행한다.

Brown and Forsythe, Bartlett 방법은 각각 "OBRIEN"을 "BF", "BARTLETT"으로 바꾸어 구한 것이다.

결과

1) O'Brien 검정 결과

2) Brown and Forsythe 검정 결과

3) Bartlett 검정 결과

약간의 차이들은 있지만 모두 p-value가 0.05 이상으로 귀무가설을 기각하지 못해 모분산이 서로 같다고 결론 내릴 수 있다. 

코드 정리

*라이브러리 지정하기;
LIBNAME hong "C:/Users/User/Documents/Tistory_blog";

*데이터 불러오기;
PROC IMPORT
DATAFILE="C:\Users\user\Documents\Tistory_blog\Data.xlsx"
DBMS=EXCEL
OUT=hong.df
REPLACE;
RUN;

*O'Brien;
PROC GLM DATA=hong.df;
   CLASS HTN;
   MODEL SBP = HTN;
   MEANS HTN / HOVTEST=OBRIEN(W=0.5);
RUN;
QUIT;

*Brown and Forsythe;
PROC GLM DATA=hong.df;
   CLASS HTN;
   MODEL SBP = HTN;
   MEANS HTN / HOVTEST=BF;
RUN;
QUIT;

*Bartlett;
PROC GLM DATA=hong.df;
   CLASS HTN;
   MODEL SBP = HTN;
   MEANS HTN / HOVTEST=BARTLETT;
RUN;
QUIT;

SAS 등분산성 검정 (Homogeneity of variance) 정복 완료!

작성일: 2022.10.05.

최종 수정일: 2022.10.05.

이용 프로그램: SAS v9.4

운영체제: Windows 10