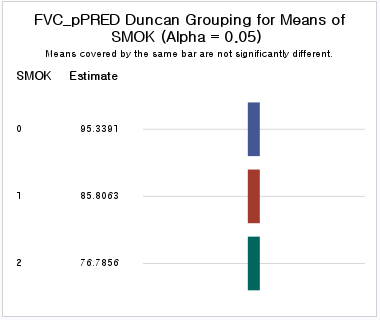
[R] 일원 배치 분산 분석 (One-way ANOVA, ANalysis Of VAriance) - aov(), pairwise.t.test(), ScheffeTest(), scheffe.test(), duncan.test(), TukeyHSD()
이전 포스팅에서 음주 여부에 따른 ALT 평균에 차이가 있는지를 알아보기 위해서는 T test를 사용한다는 내용을 알아보았다.
음주 여부는 "1) 음주자", "2) 비음주자"로 나뉘는 이분형 변수다. 즉, 음주자의 ALT 평균과 비음주자의 ALT 평균을 비교한 것이었다.
만약, 두 개 이상의 범주로 나뉘는 변수에 대해 모평균의 검정을 하고자 한다면 어떻게 해야 할까? 예를 들어, 흡연 상태를 "1) 비흡연자", "2) 과거 흡연자", "3) 현재 흡연자"로 나누었고, 각 그룹의 폐기능 검사 중 하나인 FVC (Forced Vital Capacity)의 평균에 차이가 있는지 알아보고자 한다.
이때 사용할 수 있는 방법이 일원 배치 분산 분석인 One-way ANOVA (Analysis of Variance)이며 이번 포스팅에서 다뤄볼 주된 내용이다.
*실습용 데이터는 아래 링크를 클릭하면 다운로드할 수 있습니다.
2022.08.04 - [공지사항 및 소개] - 분석용 데이터 (update 22.11.21)
분석용 데이터 (update 22.11.21)
2022년 11월 21일 버전입니다. 변수는 계속하여 추가될 예정입니다. 다음 카테고리에 있는 글에서 이용된 데이터입니다. - 기술 통계 - 범주형 자료 분석 - 모평균 검정 - 반복 측정 자료 분석 - 통계
medistat.tistory.com
코드를 보여드리기에 앞서 워킹 디렉토리부터 지정하겠다.
워킹 디렉토리에 관한 설명은 다음 링크된 포스트에서 볼 수 있다.
2022.08.05 - [통계 프로그램 사용 방법/R] - [R] 작업 디렉토리 (Working Directory) 지정 - getwd(), setwd()
setwd("C:/Users/user/Documents/Tistory_blog")
데이터를 불러와 df에 객체로 저장하겠다.
데이터 불러오는 방법은 다음 링크에서 볼 수 있다.
2022.08.05 - [통계 프로그램 사용 방법/R] - [R] 데이터 불러오기 : EXCEL - read_excel(), read.xlsx()
2022.08.10 - [통계 프로그램 사용 방법/R] - [R] 데이터 저장하기 : CSV 파일 - write.csv(), write_csv()
2022.08.10 - [통계 프로그램 사용 방법/R] - [R] 데이터 불러오기 : SAS file (.sas7bdat) - read.sas7bdat(), read_sas()
install.packages("readr")
library("readr")
df<-read_csv("Data.csv")
목표: 흡연 상태에 따라 FVC 평균은 서로 다르다고 모집단 수준에서 말할 수 있는가?
전제조건 (정규성, 등분산성)
ANOVA에는 두 가지 전제조건이 필요하다. 본 포스팅의 예시에 맞추어 설명하면 다음과 같다.
1) 정규성: 현재 흡연자, 과거 흡연자, 비흡연자 별로 FVC의 분포를 보았을 때 각각의 분포는 정규성을 따른다.
2) 등분산성: 현재 흡연자, 과거 흡연자, 비흡연자 별로 FVC의 분포를 보았을 때 분산은 서로 같다.
따라서 각각을 검정해야 한다.
전제조건 (정규성) - 코드
일원 배치 분산 분석 (One-way ANOVA)의 첫 번째 전제조건은 각각의 독립 표본의 분포가 정규성을 따른다는 것이다. 즉, 여기에서는 흡연 상태 (비흡연자, 과거 흡연자, 현재 흡연자)에 따라 수축기 혈압 (SBP)의 정규성을 검정하도록 하겠다.
따라서 다음 두 가지의 일을 해야 한다.
1) 흡연 상태 (비흡연자, 과거 흡연자, 현재 흡연자)에 따라 데이터를 나누기
나누는 방법에 대한 설명은 다음 링크에서 볼 수 있다. 2022.11.10 - [통계 프로그램 사용 방법/R] - [R] 조건에 맞는 자료 추출하기
위 링크에서 확인할 수 있듯이 여러 가지 방법으로 나눌 수 있지만 indexing을 이용하여 나누도록 하겠다.
df_ns<-df[df$SMOK==0,]
df_fs<-df[df$SMOK==1,]
df_cs<-df[df$SMOK==2,]df_ns : 비흡연자로 이루어진 데이터
df_fs : 과거 흡연자로 이루어진 데이터
df_cs : 현재 흡연자로 이루어진 데이터
2) 흡연 상태 (비흡연자, 과거 흡연자, 현재 흡연자)에 따라 정규성을 검정하기
정규성 검정에 관한 내용은 다음 링크에서 확인할 수 있다.
2022.08.11 - [기술 통계/R] - [R] 정규성 검정 (1) : Q-Q plot - qqnorm(), qqline()
2022.08.11 - [기술 통계/R] - [R] 정규성 검정 (2) : 히스토그램 - hist(), dnorm()
2022.08.12 - [기술 통계/R] - [R] 정규성 검정 (4) : 정량적 검정 (Lilliefors test) - lillie.test()
2022.08.16 - [기술 통계/R] - [R] 고급 Q-Q Plot - Van der Waerden, Rankit, Tukey, Blom
##비흡연자의 FVC 정규성 검정
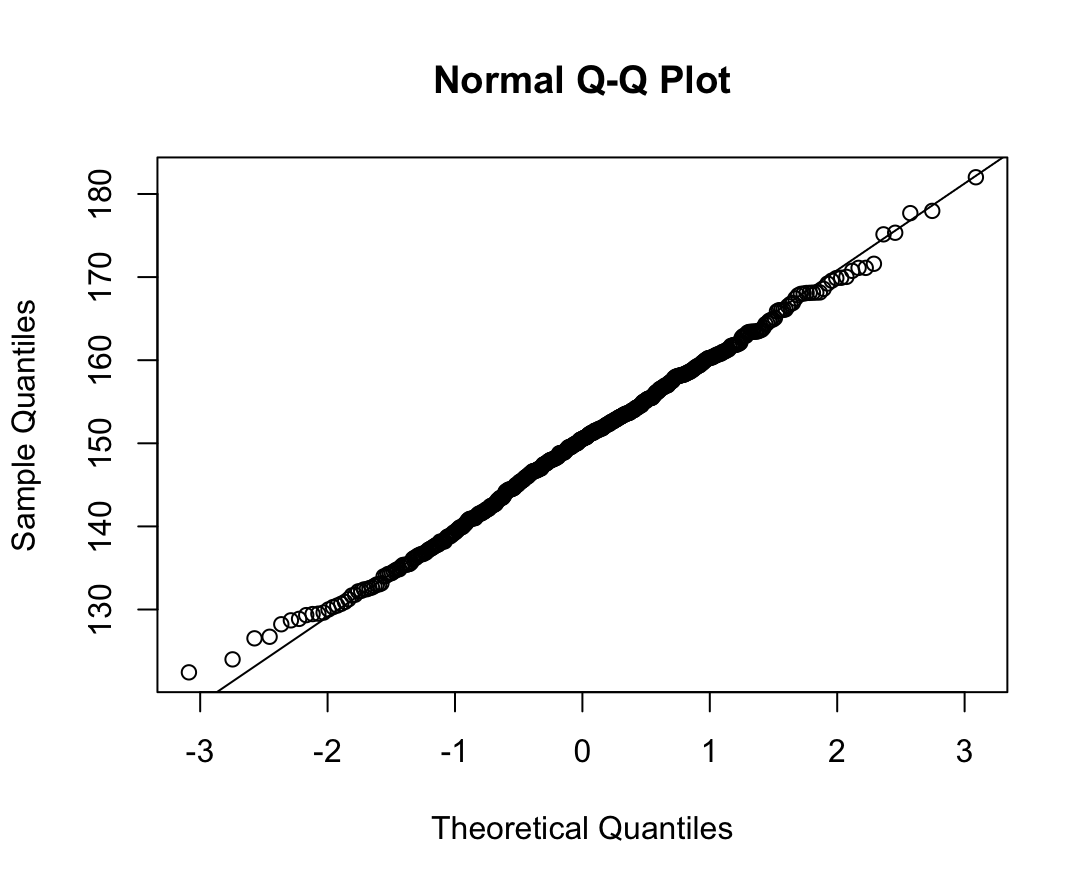
# 1) Q-Q plot 그리기
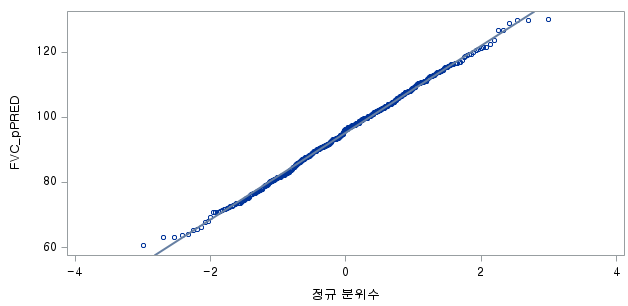
qqnorm(df_ns$FVC_pPRED)
qqline(df_ns$FVC_pPRED)
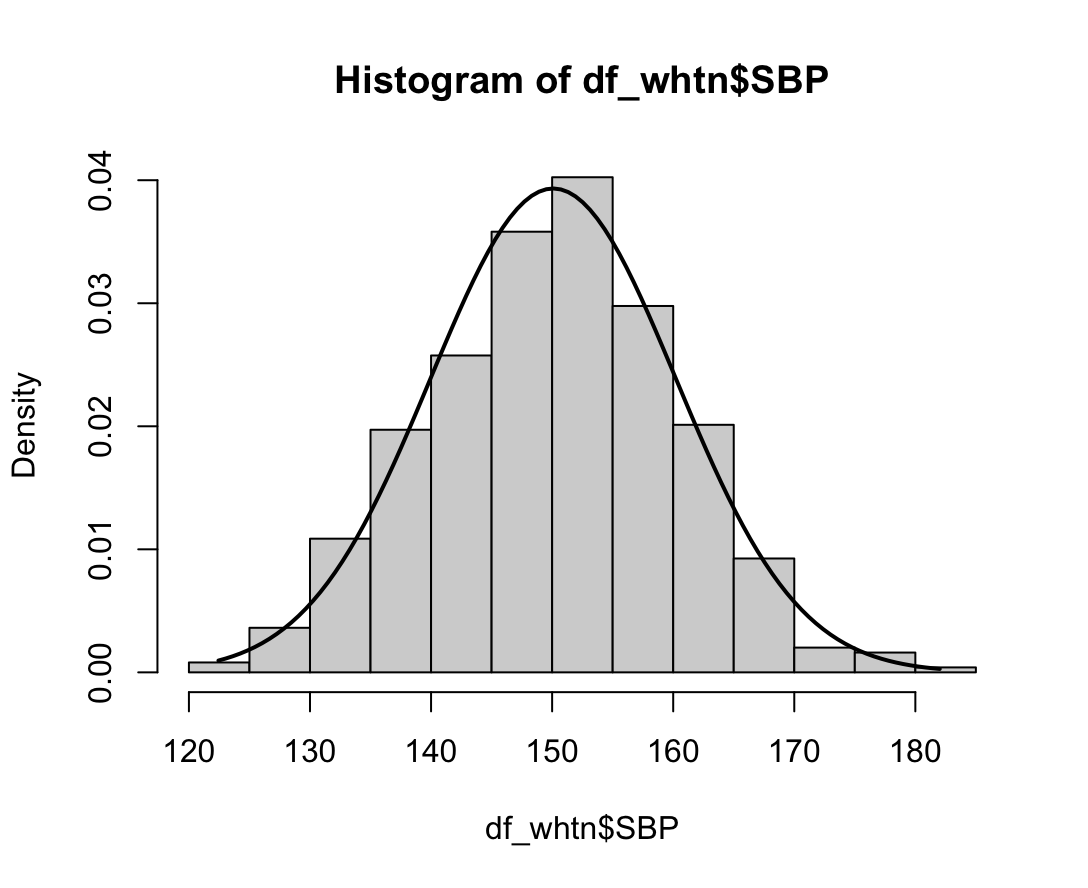
# 2) 히스토그램 그리기
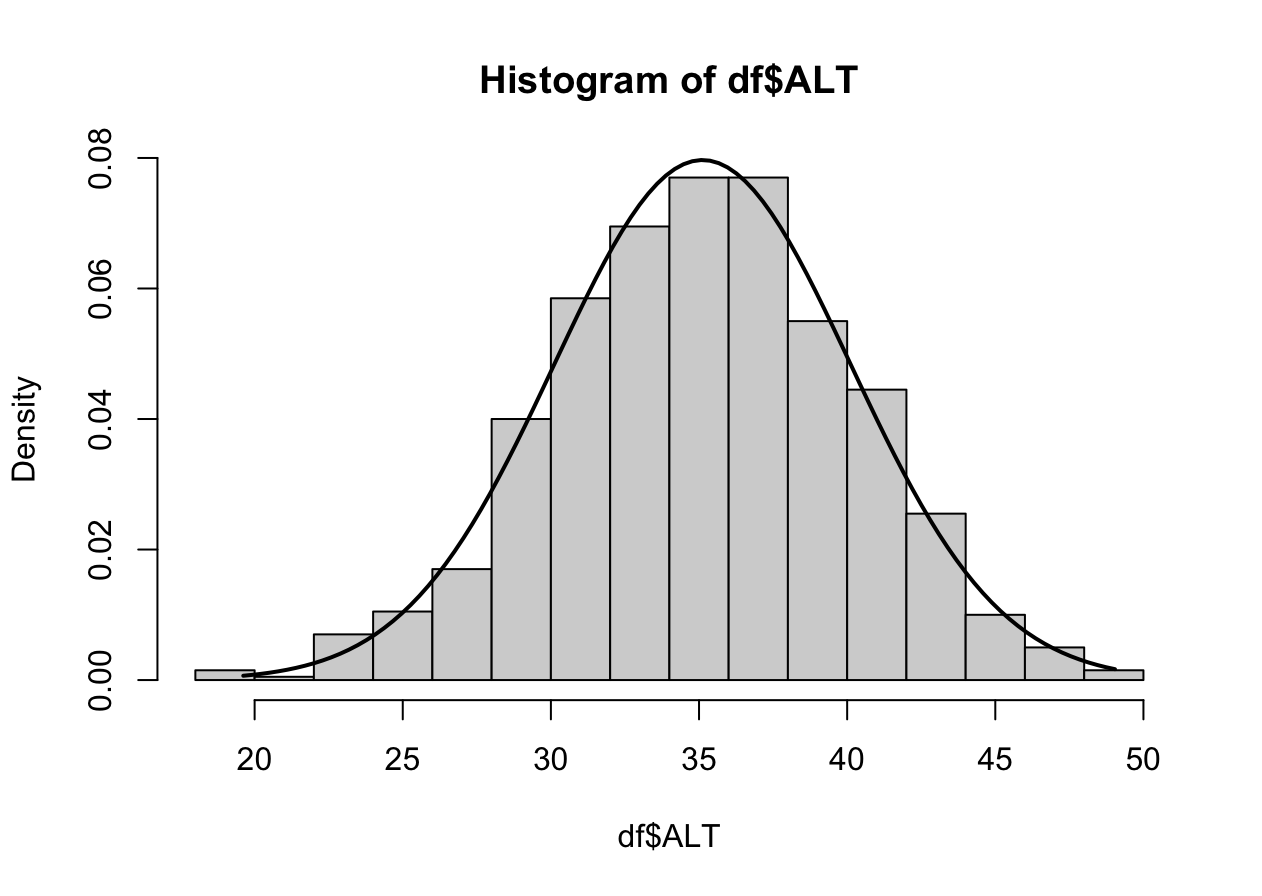
hist(df_ns$FVC_pPRED, prob=TRUE)
FVC_pPREDrange<-seq(min(df_ns$FVC_pPRED),max(df_ns$FVC_pPRED),length=max(max(df_ns$FVC_pPRED)-min(df_ns$FVC_pPRED),100))
ND<-dnorm(FVC_pPREDrange,mean=mean(df_ns$FVC_pPRED),sd=sd(df_ns$FVC_pPRED))
lines(FVC_pPREDrange, ND, lwd=2)
# 3) Shapiro-Wilk test 시행하기
shapiro.test(df_ns$FVC_pPRED)
##과거 흡연자의 FVC 정규성 검정
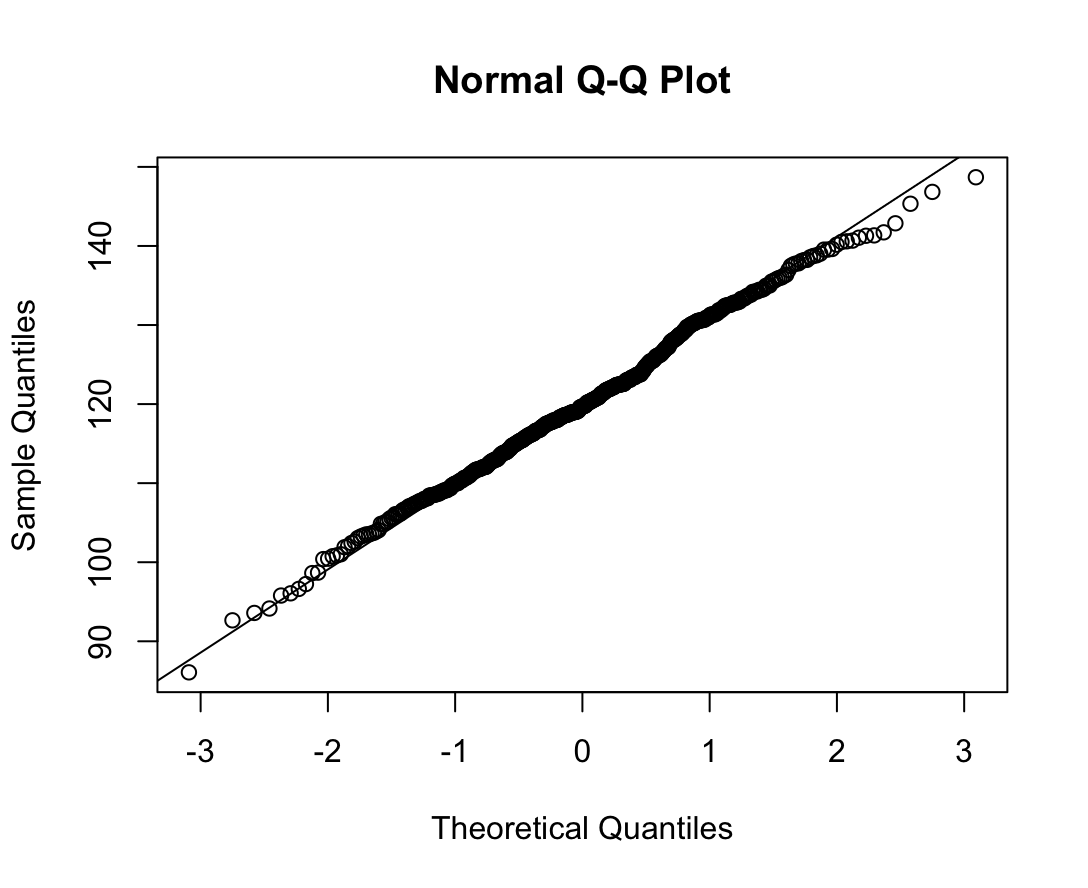
# 1) Q-Q plot 그리기
qqnorm(df_fs$FVC_pPRED)
qqline(df_fs$FVC_pPRED)
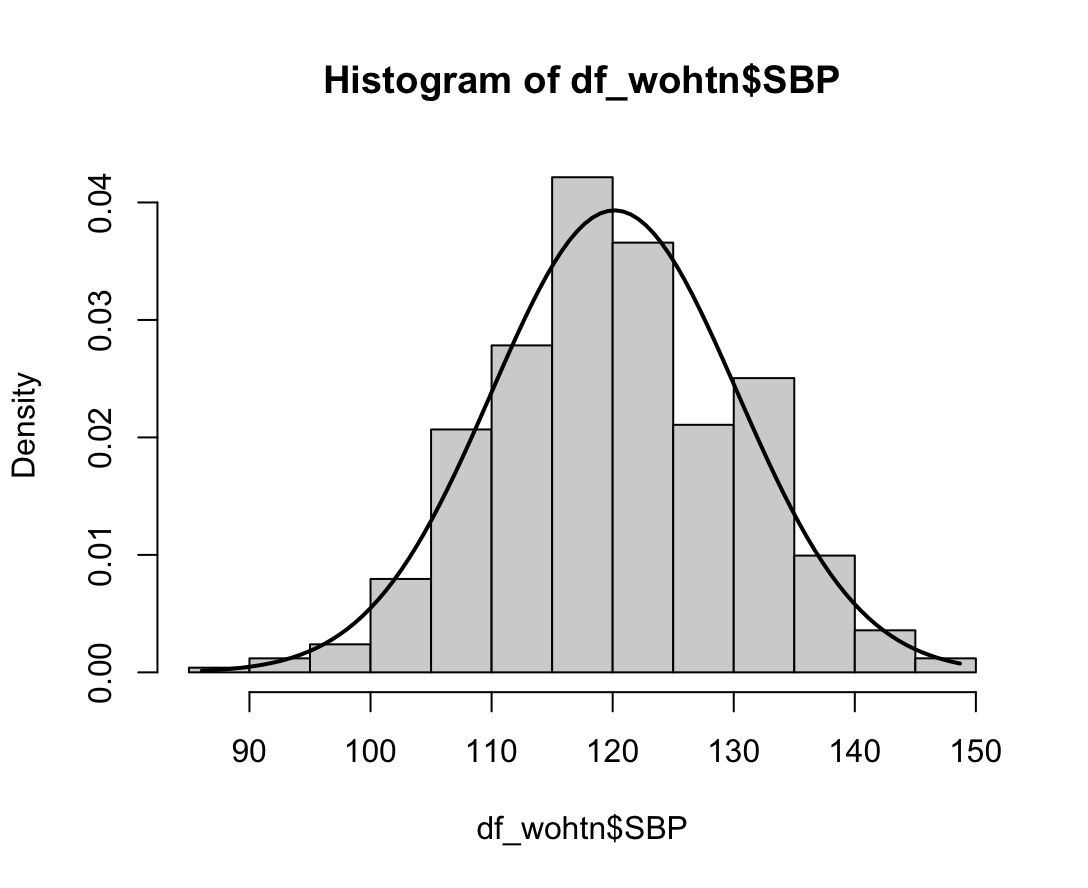
# 2) 히스토그램 그리기
hist(df_fs$FVC_pPRED, prob=TRUE)
FVC_pPREDrange<-seq(min(df_fs$FVC_pPRED),max(df_fs$FVC_pPRED),length=max(max(df_fs$FVC_pPRED)-min(df_fs$FVC_pPRED),100))
ND<-dnorm(FVC_pPREDrange,mean=mean(df_fs$FVC_pPRED),sd=sd(df_fs$FVC_pPRED))
lines(FVC_pPREDrange, ND, lwd=2)
# 3) Shapiro-Wilk test 시행하기
shapiro.test(df_fs$FVC_pPRED)
##과거 흡연자의 FVC 정규성 검정
# 1) Q-Q plot 그리기
qqnorm(df_cs$FVC_pPRED)
qqline(df_cs$FVC_pPRED)
# 2) 히스토그램 그리기
hist(df_cs$FVC_pPRED, prob=TRUE)
FVC_pPREDrange<-seq(min(df_cs$FVC_pPRED),max(df_cs$FVC_pPRED),length=max(max(df_cs$FVC_pPRED)-min(df_cs$FVC_pPRED),100))
ND<-dnorm(FVC_pPREDrange,mean=mean(df_cs$FVC_pPRED),sd=sd(df_cs$FVC_pPRED))
lines(FVC_pPREDrange, ND, lwd=2)
# 3) Shapiro-Wilk test 시행하기
shapiro.test(df_cs$FVC_pPRED)
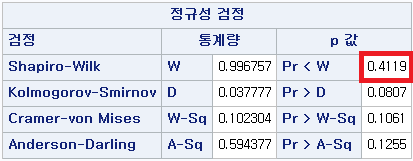
정규성 검정 - 결과
1) 비흡연자
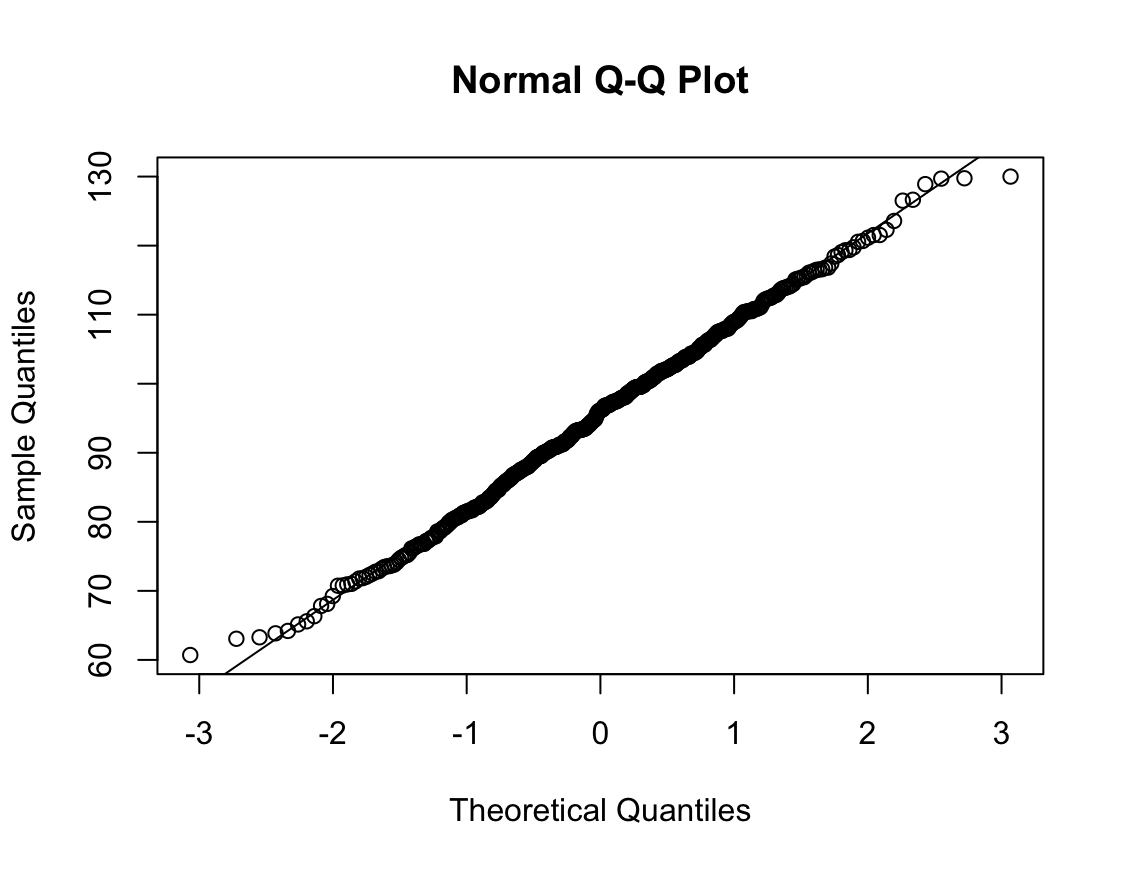
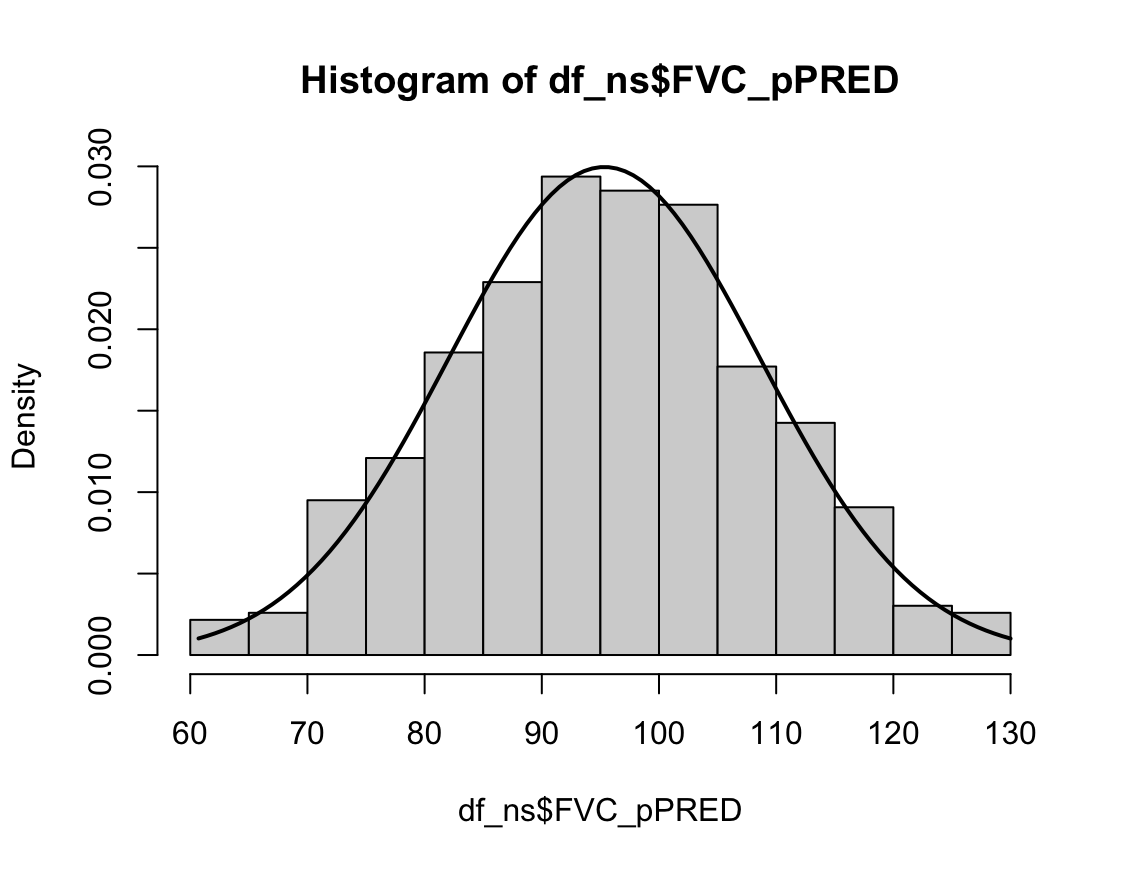
Shapiro-Wilk normality test
data: df_ns$FVC_pPRED
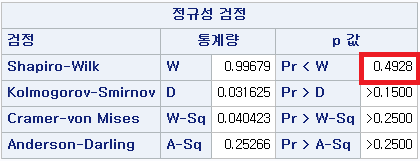
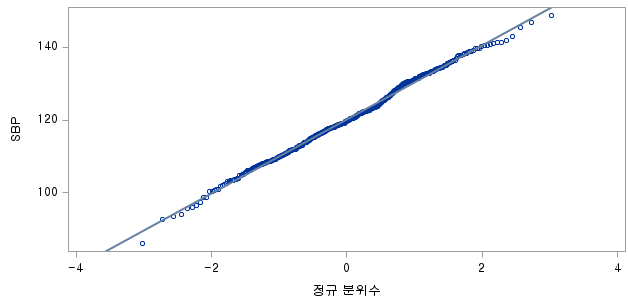
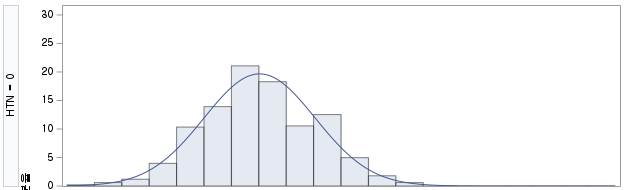
W = 0.99679, p-value = 0.4928N수가 2,000개 미만이므로 Shapiro-Wilk 통계량의 p-value를 보면 0.05 이상이며, Q-Q Plot은 대부분의 데이터가 선상에 있고, 히스토그램에서도 정규성을 따르는 것처럼 볼 수 있다.
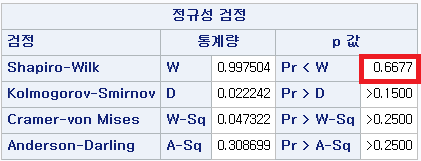
2) 과거 흡연자
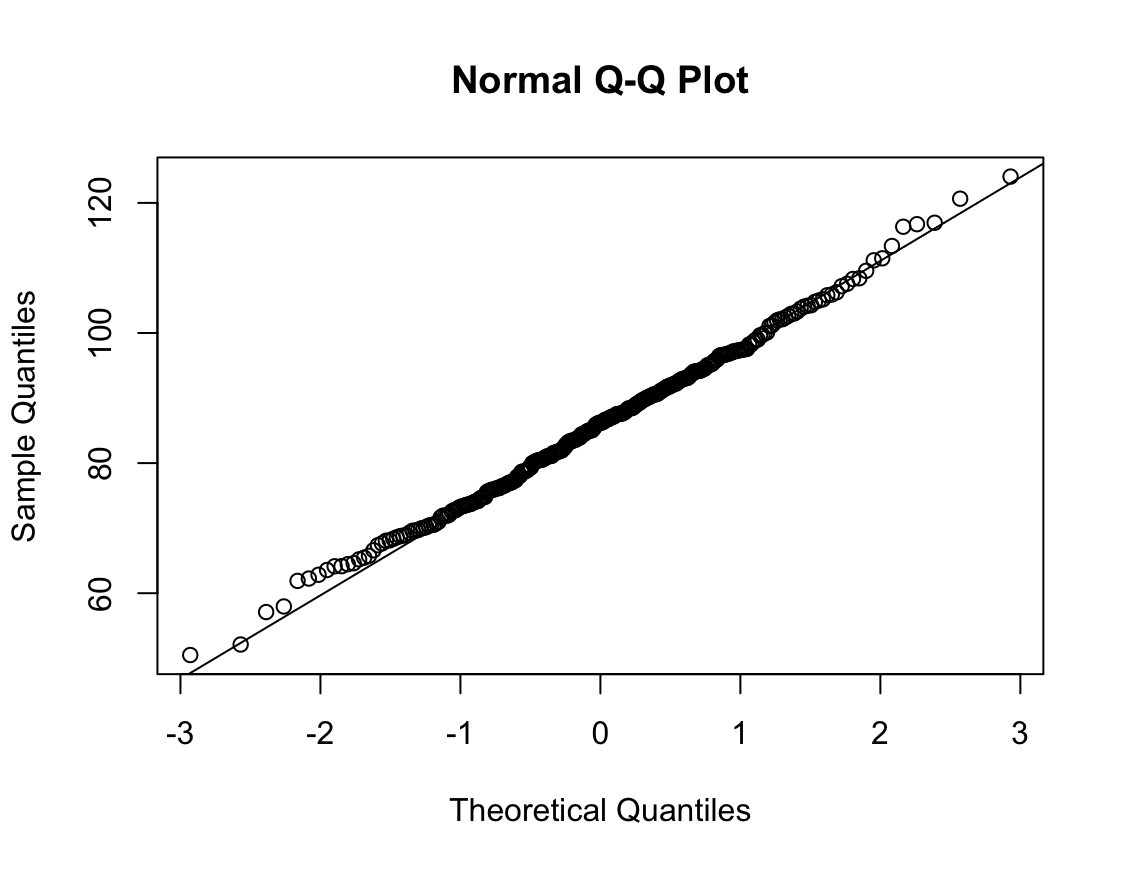
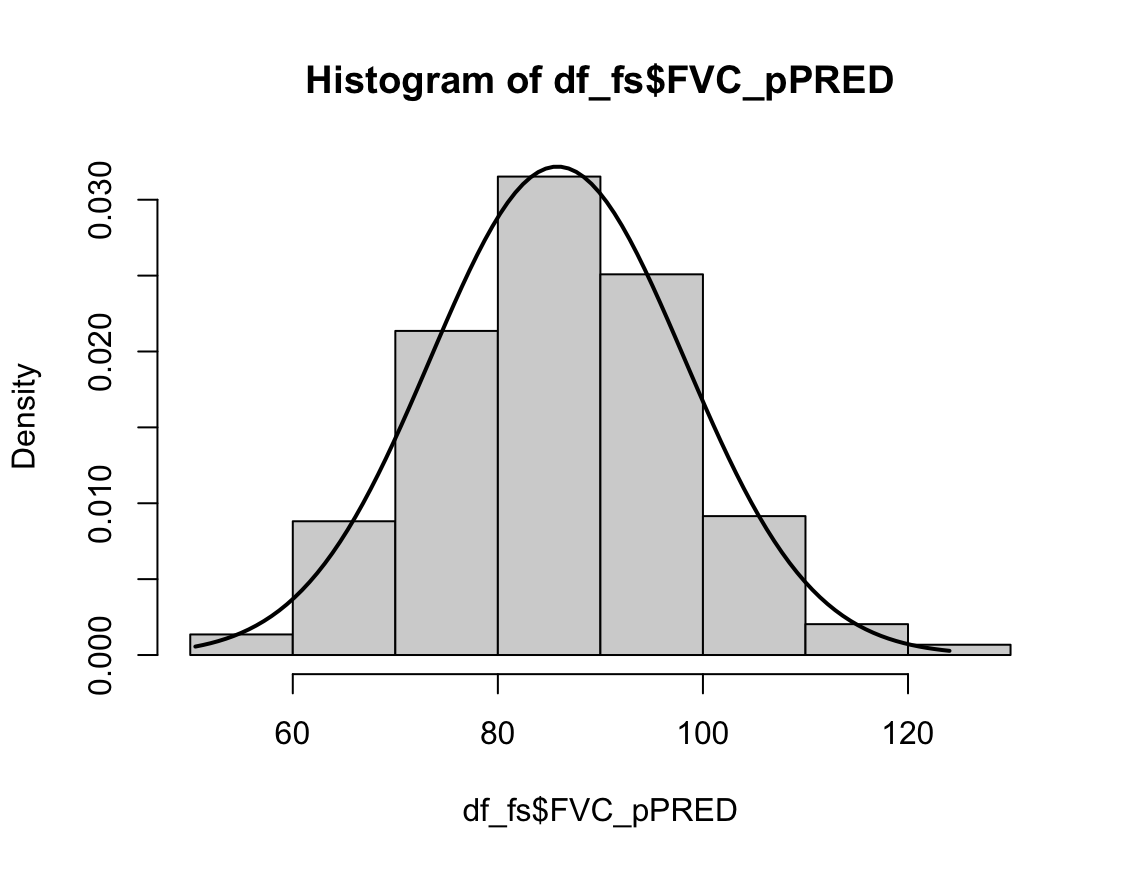
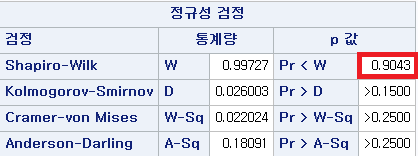
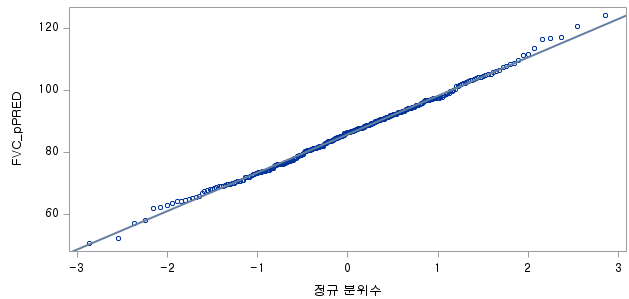
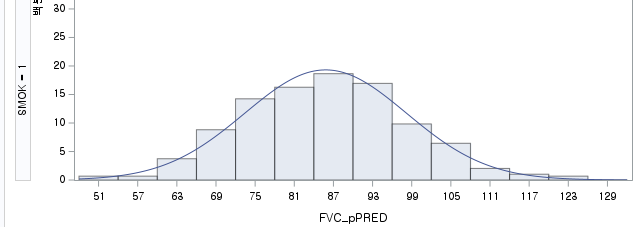
Shapiro-Wilk normality test
data: df_fs$FVC_pPRED
W = 0.99727, p-value = 0.9043N수가 2,000개 미만이므로 Shapiro-Wilk 통계량의 p-value를 보면 0.05 이상이며, Q-Q Plot은 대부분의 데이터가 선상에 있고, 히스토그램에서도 정규성을 따르는 것처럼 볼 수 있다.
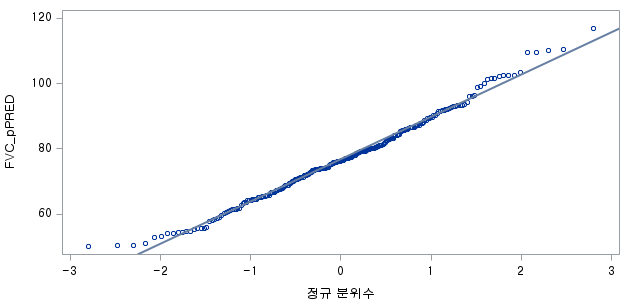
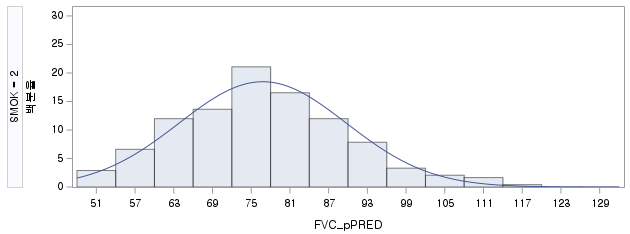
3) 현재 흡연자

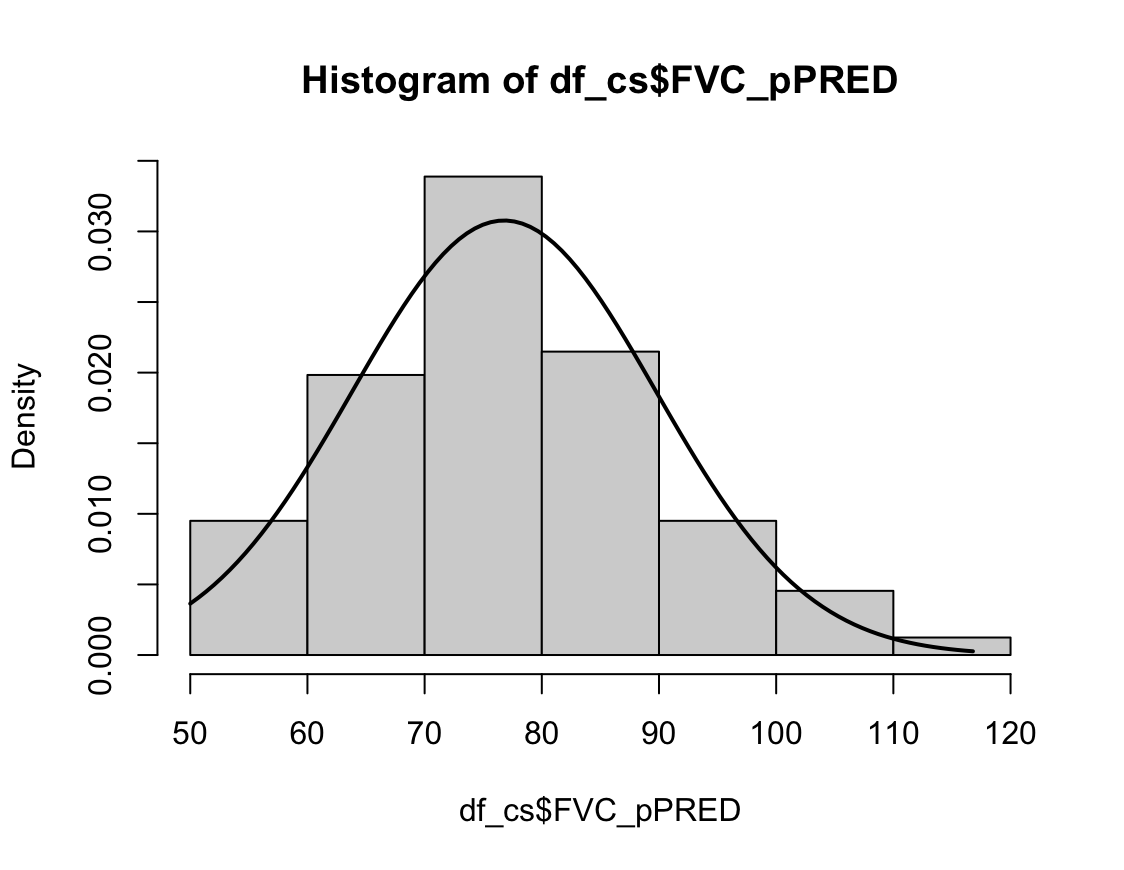
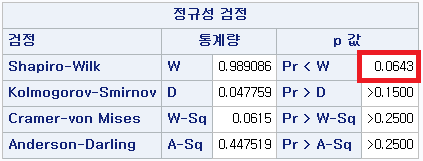
Shapiro-Wilk normality test
data: df_cs$FVC_pPRED
W = 0.98909, p-value = 0.06429N수가 2,000개 미만이므로 Shapiro-Wilk 통계량의 p-value를 보면 0.05 이상이며, Q-Q Plot은 대부분의 데이터가 선상에 있고, 히스토그램에서도 정규성을 따르는 것처럼 볼 수 있다.
첫 번째 전제조건이 성립한다. 즉, 흡연 상태에 따른 FVC의 분포가 정규성을 따른다고 할 수 있다.
2) 등분산성
등분산성 검정에 관한 내용은 다음 링크에서 확인할 수 있다.
2022.11.20 - [모평균 검정/R] - [R] 등분산성 검정 (Homogeneity of variance) - levene.test(), bartlett.test()
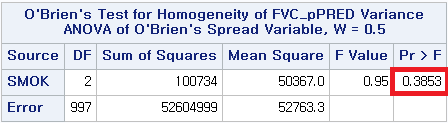
많이들 사용하는 등분산 검정 다섯 가지 중 F test는 그룹이 2개일 때에만 사용 가능하고, O'brien은 R에서 시행 불가하므로, 나머지 3가지 방법으로 검정해본다.
1) F test (그룹이 2개일 때에만 사용 가능)
2) Levene의 등분산 검정
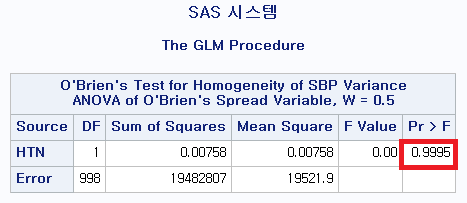
3) O'Brien의 등분산 검정(R에서 검정 불가)
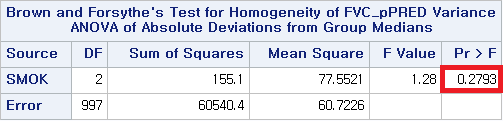
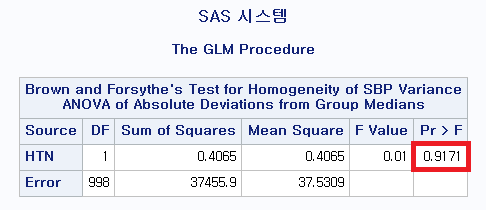
4) Brown and Forsythe의 등분산 검정
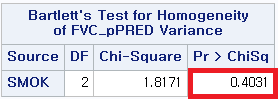
5) Bartlett의 등분산 검정
코드
#Levene의 등분산 검정
install.packages("lawstat")
library("lawstat")
levene.test(df$FVC_pPRED, df$SMOK, location="mean")
#Brown&Forsythe
install.packages("lawstat")
library("lawstat")
levene.test(df$FVC_pPRED, df$SMOK)
#Bartlett
bartlett.test(df$FVC_pPRED, df$SMOK)
결과
Classical Levene's test based on the absolute deviations
from the mean ( none not applied because the location is
not set to median )
data: df$FVC_pPRED
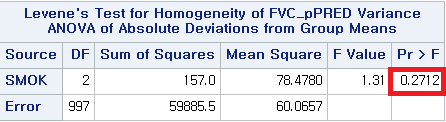
Test Statistic = 1.3065, p-value = 0.2712
Modified robust Brown-Forsythe Levene-type test based on
the absolute deviations from the median
data: df$FVC_pPRED
Test Statistic = 1.2772, p-value = 0.2793
Bartlett test of homogeneity of variances
data: df$FVC_pPRED and df$SMOK
Bartlett's K-squared = 1.8171, df = 2, p-value = 0.4031Levene 검정 (p-value: 0.2712), Brown-Forsythe test (p-value: 0.2793), Bartlett test (p-value: 0.4031)로 모두 0.05보다 큰 p-value를 갖는다. 따라서 귀무가설을 기각하지 못하므로, 흡연 상태에 따라 FVC_pPRED의 분산이 동일하다는 귀무가설을 채택한다.
따라서 ANOVA의 두 가지 전제조건 (정규성, 등분산성)이 성립하므로 ANOVA를 실행할 수 있다.
범주형 변수로의 변환
ANOVA를 시행하기 앞서, df데이터의 SMOK변수는 "비흡연자", "과거 흡연자", "현재 흡연자"를 각각 0,1,2로 코딩한 범주형 변수임을 R에게 알려주어야 한다. 알려주지 않으면 0, 1, 2로 이루어진 숫자형 변수로 인식하고 있기 때문이다. 따라서 변수의 유형을 범주형으로 바꾸어준다. (상세한 내용은 다음 링크를 확인하길 바란다.2022.11.21 - [통계 프로그램 사용 방법/R] - [R] 변수의 유형 (타입, type) 확인 및 변경 - as.factor(), as.numeric(), as.character(), str())
df$SMOK<-as.factor(df$SMOK)
일원 배치 분산 분석 (One-way ANOVA) 시행
코드
a<-aov(FVC_pPRED~SMOK, data=df)
summary(a)a<-aov(FVC_pPRED~SMOK, data=df) : df 데이터의 SMOK에 따른 FVC_pPRED의 평균이 서로 다른지 ANOVA를 시행하고, 이를 a라는 객체에 저장하라.
summary(a) : a를 요약하여 보여달라.
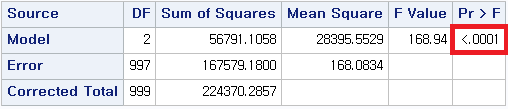
결과
Df Sum Sq Mean Sq F value Pr(>F)
SMOK 2 56791 28396 168.9 <2e-16 ***
Residuals 997 167579 168
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Df Sum Sq Mean Sq F value Pr(>F)
SMOK 2 56791 28396 168.9 <2e-16 ***
Residuals 997 167579 168
결과는 복잡하지만 우리가 볼 곳은 빨간 글씨로 칠해놓은 단 하나의 값, p-value다. 값은 2×10−16보다 작으므로 이는 0.05보다 한참 작은 값이므로 귀무가설을 기각하고 대립 가설을 채택한다. 그렇다면 여기에서 귀무가설 및 대립 가설은 무엇이었는가?
귀무가설: H0= 세 집단의 모평균은 "모두" 동일하다.
대립 가설: H1= 세 집단의 모평균이 모두 동일한 것은 아니다.
우리는 대립 가설을 채택해야 하므로 "세 집단의 모평균이 모두 동일한 것은 아니다."라고 결론 내릴 것이다.
이 말은, 세 집단 중 두 개씩 골라 비교했을 때, 적어도 한 쌍에서는 차이가 난다는 것이다. 따라서 세 집단 중 두 개씩 골라 비교를 해보아야 하며, 이를 사후 분석 (post hoc analysis)이라고 한다. 세 집단에서 두 개씩 고르므로 가능한 경우의 수는 3C2=3이다.
(1) 비흡연자 vs 과거 흡연자
(2) 비흡연자 vs 현재 흡연자
(3) 과거 흡연자 vs 현재 흡연자
사후 분석을 시행하겠다.
SAS를 이용한 ANOVA에 관한 글(2022.10.12 - [모평균 검정/SAS] - [SAS] 일원 배치 분산 분석 (One-way ANOVA, ANalysis Of VAriance) - PROC GLM, PROC ANOVA)에서 많은 사후 분석 방법이 있음을 밝혔고, 많이 사용되는 방법들에 대해서도 언급하였다. 본 포스팅에서는 많이 사용되는 다음 네 가지 사후 분석 방법을 소개한다.
1) Bonferroni t test
2) Scheffe's multiple comparison
3) Duncan's multiple range test
4) Tukey's studentized range test
1) Bonferroni t test - 코드
pairwise.t.test(df$FVC_pPRED, df$SMOK, p.adj="bonferroni")pairwise.t.test(df$FVC_pPRED, df$SMOK, p.adj="bonferroni") :df 데이터의 FVC_pPRED를 SMOK변수값에 따라 각각 t-test를 시행하는데, p-value는 Bonferroni방식으로 보정하라.
결과
Pairwise comparisons using t tests with pooled SD
data: df$FVC_pPRED and df$SMOK
0 1
1 < 2e-16 -
2 < 2e-16 8.7e-15
P value adjustment method: bonferroni Pairwise comparisons using t tests with pooled SD
data: df$FVC_pPRED and df$SMOK
| 0 | 1 | |
| 1 | <2e-16 | - |
| 2 | <2e-16 | 8.7e-15 |
P value adjustment method: bonferroni
결과가 복잡해 보일지라도 우리는 표만 잘 보면 된다.
SMOK에는 3가지 값 (비흡연자:0, 과거 흡연자:1, 현재 흡연자:2)이 들어있고, 이 중 둘을 뽑아 t-test를 시행할 것이다. 따라서 3개 중 2개를 뽑는 경우의 수인 3가지 p-value가 존재하게 된다.
비흡연자(0)와 과거 흡연자(1)를 비교한 p-value는 빨간색으로 표시된 "<2e-16"이다.
비흡연자(0)와 현재 흡연자(2)를 비교한 p-value는 초록색으로 표시된 "<2e-16"이다.
과거 흡연자(1)와 현재 흡연자(2)를 비교한 p-value는 파란색으로 표시된 "8.7e-15"이다.
즉, 모든 조합에서 평균의 차이가 있다고 결론 내릴 수 있다.
따라서, 우리가 채택한 대립 가설 "세 집단의 모평균이 모두 동일한 것은 아니다."을 구체적으로 이야기하면 "비흡연자와 과거 흡연자, 비흡연자와 현재 흡연자, 과거 흡연자와 현재 흡연자 사이의 모평균에 차이가 있다."라고 결론내릴 수 있다.
2) Scheffe's multiple comparison - 코드 (방법 1)
install.packages("DescTools")
library("DescTools")
ScheffeTest(a)ScheffeTest(a) :a(ANOVA 시행한 것)의 사후 분석을 Scheffe test로 시행하라.
이 함수는 "DecsTools"라는 패키지를 필요로 하므로 설치 후 사용하길 바란다.
결과
Posthoc multiple comparisons of means: Scheffe Test
95% family-wise confidence level
$SMOK
diff lwr.ci upr.ci pval
1-0 -9.532840 -11.90048 -7.165204 < 2e-16 ***
2-0 -18.553484 -21.07451 -16.032453 < 2e-16 ***
2-1 -9.020644 -11.77709 -6.264193 2.9e-14 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Posthoc multiple comparisons of means: Scheffe Test
95% family-wise confidence level
$SMOK
diff lwr.ci upr.ci pval
1-0 -9.532840 -11.90048 -7.165204 < 2e-16 ***
2-0 -18.553484 -21.07451 -16.032453 < 2e-16 ***
2-1 -9.020644 -11.77709 -6.264193 2.9e-14 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
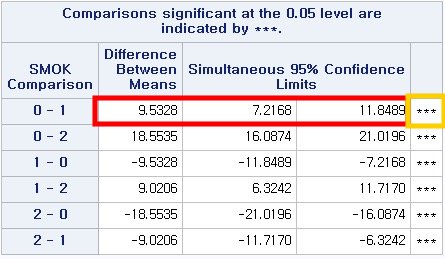
결과가 복잡해 보일지라도 우리는 표만 잘 보면 된다.
SMOK에는 3가지 값 (비흡연자:0, 과거 흡연자:1, 현재 흡연자:2)이 들어있고, 이 중 둘을 뽑아 사후 검정을 시행할 것이다. 따라서 3개 중 2개를 뽑는 경우의 수인 3가지 p-value가 존재하게 된다.
비흡연자(0)와 과거 흡연자(1)를 비교한 p-value는 빨간색으로 표시된 "<2e-16"이다.
비흡연자(0)와 현재 흡연자(2)를 비교한 p-value는 초록색으로 표시된 "<2e-16"이다.
과거 흡연자(1)와 현재 흡연자(2)를 비교한 p-value는 파란색으로 표시된 "2.9e-14"이다.
즉, 모든 조합에서 평균의 차이가 있다고 결론 내릴 수 있다.
2-1) Scheffe's multiple comparison - 코드 (방법 2)
install.packages("agricolae")
library(agricolae)
scheffe.test(a,"SMOK",console=TRUE)"agriocolae"패키지에 있는 scheffe.test() 함수를 이용할 수도 있다.
scheffe.test(a,"SMOK",console=TRUE) : a(ANOVA 시행한 것)에서 "SMOK"변수에 따라 Scheffe test를 시행하고 결과를 보여달라(console=TRUE).
결과
Study: a ~ "SMOK"
Scheffe Test for FVC_pPRED
Mean Square Error : 168.0834
SMOK, means
FVC_pPRED std r Min Max
0 95.33911 13.31491 463 60.70763 130.0000
1 85.80627 12.39528 295 50.49873 124.0448
2 76.78563 12.96366 242 50.00000 116.7888
Alpha: 0.05 ; DF Error: 997
Critical Value of F: 3.004752
Groups according to probability of means differences and alpha level( 0.05 )
Means with the same letter are not significantly different.
FVC_pPRED groups
0 95.33911 a
1 85.80627 b
2 76.78563 c너무나도 복잡해 보이지만, 마지막 결과를 예쁘게 제시해주기 때문에 이 함수를 소개한 것이다.
| groups | |
| 0 | a |
| 1 | b |
| 2 | c |
0은 group a, 1은 group b, 2는 group c에 속한다. 즉 서로 다른 모평균을 갖는다고 결론 내릴 수 있다.
만약 유의미한 차이가 없는 경우 어떻게 제시될까?
df$RESID<-as.factor(df$RESID)
b<-aov(FVC_pPRED~RESID, data=df)
scheffe.test(b,"RESID",console=TRUE)SMOK가 아니라 RESID에 대해 ANOVA를 시행하고, Scheffe test를 시행한 결과다.
Study: b ~ "RESID"
Scheffe Test for FVC_pPRED
Mean Square Error : 219.1342
RESID, means
FVC_pPRED std r Min Max
0 84.73360 14.84186 323 50.32614 129.7551
1 88.59510 15.17535 335 50.00000 129.7026
2 90.61014 14.39179 342 50.47718 130.0000
Alpha: 0.05 ; DF Error: 997
Critical Value of F: 3.004752
Groups according to probability of means differences and alpha level( 0.05 )
Means with the same letter are not significantly different.
FVC_pPRED groups
2 90.61014 a
1 88.59510 a
0 84.73360 b| groups | |
| 0 | a |
| 1 | a |
| 2 | b |
위 표를 보면 비흡연자 (0)과 과거 흡연자 (1)은 모두 group a에 속해있다. 즉 비흡연자와 과거 흡연자 사이에는 유의미한 차이가 발견되지 않은 것이다. 반면 현재 흡연자는 group b에 속해있으므로 비흡연자나 과거 흡연자와는 유의미한 차이가 있었다는 것이다.
3) Duncan's multiple range test - 코드
사실 Tukey나 다음에 나오는 Duncan은 각 그룹별 표본의 수가 같을 때 사용하는 것이므로 이 데이터의 사후 분석으로는 적절하지 않다. 하지만 우선 그냥 시행해보겠다.
install.packages("agricolae")
library(agricolae)
duncan.test(a,"SMOK",console=TRUE)"agriocolae"패키지에 있는 duncan.test() 함수를 이용하므로 설치부터 한다.
duncan.test(a,"SMOK",console=TRUE) : a(ANOVA 시행한 것)에서 "SMOK"변수에 따라 Duncan test를 시행하고 결과를 보여달라(console=TRUE).
결과
Study: a ~ "SMOK"
Duncan's new multiple range test
for FVC_pPRED
Mean Square Error: 168.0834
SMOK, means
FVC_pPRED std r Min Max
0 95.33911 13.31491 463 60.70763 130.0000
1 85.80627 12.39528 295 50.49873 124.0448
2 76.78563 12.96366 242 50.00000 116.7888
Groups according to probability of means differences and alpha level( 0.05 )
Means with the same letter are not significantly different.
FVC_pPRED groups
0 95.33911 a
1 85.80627 b
2 76.78563 c마지막 세 줄을 보면 0은 group a, 1은 group b, 2는 group c에 속한다. 즉 서로 다른 모평균을 갖는다고 결론 내릴 수 있다.
4) Tukey's studentized range test
TukeyHSD(a)TukeyHSD(a) : a (ANOVA 시행한 것)으로 사후 분석을 시행하되 Tukey test를 사용하라.
결과
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = FVC_pPRED ~ SMOK, data = df)
$SMOK
diff lwr upr p adj
1-0 -9.532840 -11.79982 -7.265858 0
2-0 -18.553484 -20.96734 -16.139628 0
2-1 -9.020644 -11.65991 -6.381377 0 Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = FVC_pPRED ~ SMOK, data = df)
$SMOK
diff lwr upr p adj
1-0 -9.532840 -11.79982 -7.265858 0
2-0 -18.553484 -20.96734 -16.139628 0
2-1 -9.020644 -11.65991 -6.381377 0
결과가 복잡하지만 "p adj"만 보면 된다. 어떤 비교든 p value가 너무 작아 0으로 나타난다. 따라서, 서로 다른 모평균을 갖는다고 결론 내릴 수 있다.
이 시점에서 이런 의문이 들 수 있다.
"각각의 그룹별로 평균을 비교하면 되지, 굳이 왜 ANOVA라는 방법까지 사용하는 것인가?"
아주 논리적인 의문점이다. 하지만, 반드시 ANOVA를 사용해야 한다. 그 이유는 다음과 같다. 본 사례는 흡연 상태에 따른 조합 가능한 경우의 수가 3인데, 각각 유의성의 기준을 α=0.05로 잡아보자. 이때 세 번의 비교에서 모두 귀무가설이 학문적인 진실인데(평균에 차이가 없다.), 세 번 모두 귀무가설을 선택할 확률은 (1−0.95)3≈0.86이다. (이해가 어려우면 p-value에 대한 설명 글을 읽고 오길 바란다. 2022.09.05 - [통계 이론] - [이론] p-value에 관한 고찰)
그런데, ANOVA의 귀무가설은 "모든 집단의 평균이 같다."이다. 따라서 모든 집단의 평균이 같은 것이 학문적 진실일 때, 적어도 한 번이라도 대립 가설을 선택하게 될 확률은 1−0.86=0.14가 된다. 즉, 유의성의 기준이 올라가게 되어, 덜 보수적인 결정을 내리게 되고, 다시 말하면 대립 가설을 잘 선택하는 쪽으로 편향되게 된다. 학문적으로는 '다중 검정 (multiple testing)을 시행하면 1종 오류가 발생할 확률이 증가하게 된다.'라고 표현한다.
따라서, 각각을 비교해보는 것이 아니라 한꺼번에 비교하는 ANOVA를 시행해야 함이 마땅하다.
여기에서 한 번 더 의문이 들 수 있다.
"사후 분석을 할 때에는 1종 오류가 발생하지 않는가?"
그렇다. 1종 오류가 발생할 확률이 있으므로, p-value의 기준을 더 엄격하게 (0.05보다 더 작게) 잡아야 한다. P-value를 보정하는 방법은 여러 가지가 나와있는데, 그중 많이 쓰이는 네 가지를 언급한 것이다.
어떤 사후 분석을 쓸 것인가
이 논의에 대해 정답이 따로 있는 것은 아니다. 적절한 방법을 사용하여 논문에 제시하면 되고, 어떤 것이 정답이라고 콕 집어 이야기할 수는 없다. 다만, 사후 분석 방법이 여러 가지가 있다는 것은 '사후 분석 방법에 따라 산출되는 결과가 달라질 수 있다.'는 것을 의미하고, 심지어는 '어떤 사후 분석 방법을 채택하냐에 따라 유의성 여부가 달라질 수도 있다.'는 것을 의미한다. 심지어, ANOVA에서는 유의한 결과가 나왔는데, 사후 분석을 해보니 유의한 차이를 보이는 경우가 없을 수도 있다. 따라서 어떤 사후 분석 방법 결과에 따른 결과인지 유의하여 해석할 필요가 있다.
코드 정리
####워킹 디렉토리 지정
setwd("C:/Users/user/Documents/Tistory_blog")
####데이터 불러오기
install.packages("readr")
library("readr")
df<-read_csv("Data.csv")
####데이터 나누기
df_ns<-df[df$SMOK==0,]
df_fs<-df[df$SMOK==1,]
df_cs<-df[df$SMOK==2,]
####정규성 검정
##비흡연자의 FVC 정규성 검정
# 1) Q-Q plot 그리기
qqnorm(df_ns$FVC_pPRED)
qqline(df_ns$FVC_pPRED)
# 2) 히스토그램 그리기
hist(df_ns$FVC_pPRED, prob=TRUE)
FVC_pPREDrange<-seq(min(df_ns$FVC_pPRED),max(df_ns$FVC_pPRED),length=max(max(df_ns$FVC_pPRED)-min(df_ns$FVC_pPRED),100))
ND<-dnorm(FVC_pPREDrange,mean=mean(df_ns$FVC_pPRED),sd=sd(df_ns$FVC_pPRED))
lines(FVC_pPREDrange, ND, lwd=2)
# 3) Shapiro-Wilk test 시행하기
shapiro.test(df_ns$FVC_pPRED)
##과거 흡연자의 FVC 정규성 검정
# 1) Q-Q plot 그리기
qqnorm(df_fs$FVC_pPRED)
qqline(df_fs$FVC_pPRED)
# 2) 히스토그램 그리기
hist(df_fs$FVC_pPRED, prob=TRUE)
FVC_pPREDrange<-seq(min(df_fs$FVC_pPRED),max(df_fs$FVC_pPRED),length=max(max(df_fs$FVC_pPRED)-min(df_fs$FVC_pPRED),100))
ND<-dnorm(FVC_pPREDrange,mean=mean(df_fs$FVC_pPRED),sd=sd(df_fs$FVC_pPRED))
lines(FVC_pPREDrange, ND, lwd=2)
# 3) Shapiro-Wilk test 시행하기
shapiro.test(df_fs$FVC_pPRED)
##과거 흡연자의 FVC 정규성 검정
# 1) Q-Q plot 그리기
qqnorm(df_cs$FVC_pPRED)
qqline(df_cs$FVC_pPRED)
# 2) 히스토그램 그리기
hist(df_cs$FVC_pPRED, prob=TRUE)
FVC_pPREDrange<-seq(min(df_cs$FVC_pPRED),max(df_cs$FVC_pPRED),length=max(max(df_cs$FVC_pPRED)-min(df_cs$FVC_pPRED),100))
ND<-dnorm(FVC_pPREDrange,mean=mean(df_cs$FVC_pPRED),sd=sd(df_cs$FVC_pPRED))
lines(FVC_pPREDrange, ND, lwd=2)
# 3) Shapiro-Wilk test 시행하기
shapiro.test(df_cs$FVC_pPRED)
####등분산 검정
#Levene의 등분산 검정
install.packages("lawstat")
library("lawstat")
levene.test(df$FVC_pPRED, df$SMOK, location="mean")
#Brown&Forsythe
install.packages("lawstat")
library("lawstat")
levene.test(df$FVC_pPRED, df$SMOK)
#Bartlett
bartlett.test(df$FVC_pPRED, df$SMOK)
####범주형 변수로의 변환
df$SMOK<-as.factor(df$SMOK)
####One-way ANOVA 시행
a<-aov(FVC_pPRED~SMOK, data=df)
summary(a)
####사후분석
#1) Bonferroni t test
pairwise.t.test(df$FVC_pPRED, df$SMOK, p.adj="bonferroni")
#2) Scheffe's multiple comparison (1)
install.packages("DescTools")
library("DescTools")
ScheffeTest(a)
#2-1) Scheffe's multiple comparison (2)
install.packages("agricolae")
library(agricolae)
scheffe.test(a,"SMOK",console=TRUE)
#3) Duncan's multiple range test
install.packages("agricolae")
library(agricolae)
duncan.test(a,"SMOK",console=TRUE)
#4) Tukey's studentized range test
TukeyHSD(a)
[R] 일원 배치 분산 분석 (One-way ANOVA, ANalysis Of VAriance) 정복 완료!
작성일: 2022.11.20.
최종 수정일: 2022.11.29.
이용 프로그램: R 4.2.2
RStudio v2022.07.2
RStudio 2022.07.2+576 "Spotted Wakerobin" Release
운영체제: Windows 10, Mac OS 12.6.1