의학 통계 코드 저장소

 어떤 분포의 평균이 특정 값인지 확인하는 방법을 이전에는 일표본 T검정 (One-Sample T test)로 시행했었다. (2022.11.29 - [모평균 검정/SPSS] - [SPSS] 일표본 T검정 (One-sample T-test)) 하지만 여기에는 중요한 가정이 필요한데, 분포가 정규성을 따르는 것이다. 하지만 분포가 정규성을 따르지 않는다면 어떻게 해야 할까? 그럴 때 사용하는 것이 One-Sample Wilcoxon Signed Rank Test (일표본 윌콕슨 부호 순위 검정)이다. 

 이번 포스팅에서는 One-Sample Wilcoxon Signed Rank Test (일표본 윌콕슨 부호 순위 검정)에 대해서 알아볼 것이다.

*실습용 데이터는 아래 링크를 클릭하면 다운로드할 수 있습니다.

2022.08.04 - [공지사항 및 소개] - 분석용 데이터 (update 22.12.01)

데이터를 불러오도록 한다. 불러오는 방법은 다음 링크를 확인하도록 한다.

2022.08.04 - [통계 프로그램 사용 방법/SPSS] - [SPSS] 데이터 불러오기 및 저장하기

목표: 모집단에서 신경심리검사 1 원점수의 중앙값이 55이라고 할 수 있는가?

 이번 포스팅의 목적은 1000명의 데이터를 가지고, 이 1000명이 기원한 모집단에서 신경심리검사 1 원점수의 중앙값이 55이라고 할 수 있는지 판단하는 것이다.

전제조건 (정규성)

 만약 정규성을 따른다면 t-test를 하면 되므로 정규성 여부를 파악하도록 한다. 정규성 검정에 관한 분석 내용은 다음 글에서 살펴볼 수 있다. 

2022.08.11 - [기술 통계/SPSS] - [SPSS] 정규성 검정

2022.08.18 - [기술 통계/SPSS] - [SPSS] 고급 Q-Q Plot - Van der Waerden, Rankit, Tukey, Blom

정규성 검정

1) 분석(A) > 기술통계량(E) > 데이터 탐색 (E)

2) 분석하고자 하는 변수인 NP1_raw을 "종속변수"에 넣어준다. 그 뒤 "도표(T)..."를 선택한다.

3) "히스토그램(H)", "검정과 함께 정규성 도표(O)" 체크박스를 클릭하고 "계속(C)"를 누르고, 돌아가 "확인"을 누른다.

결과

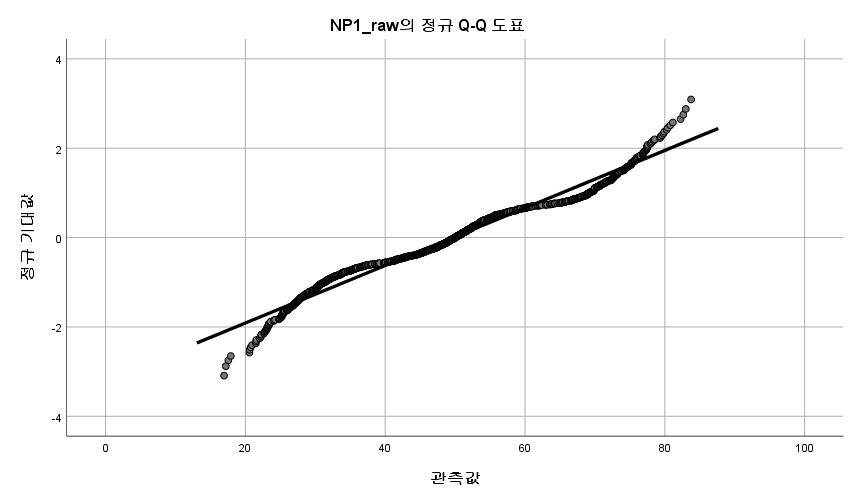
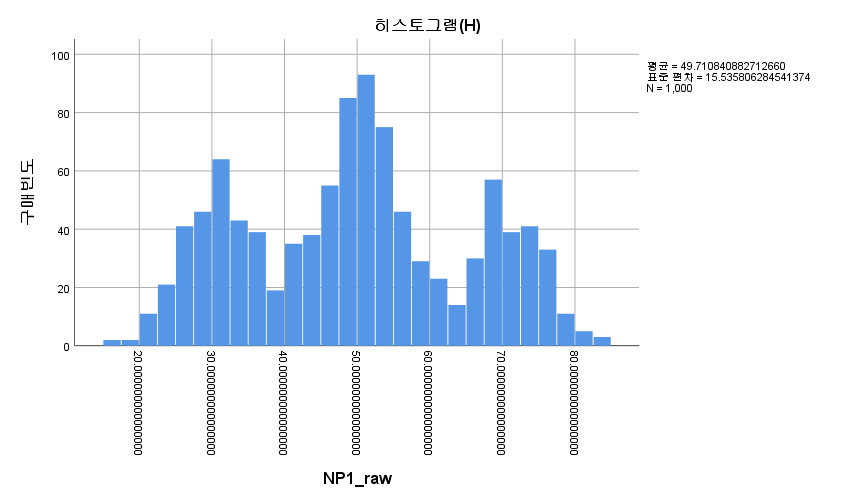
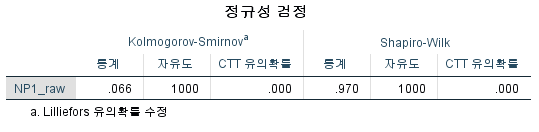
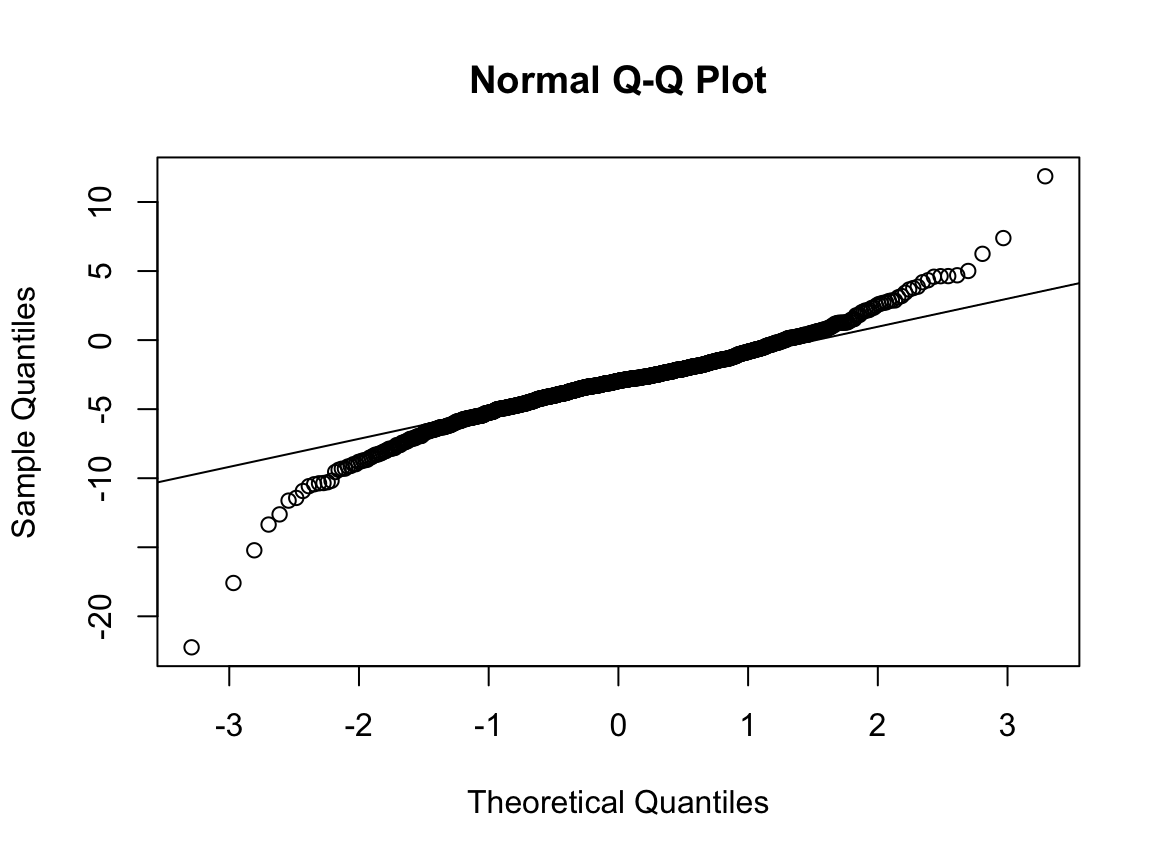
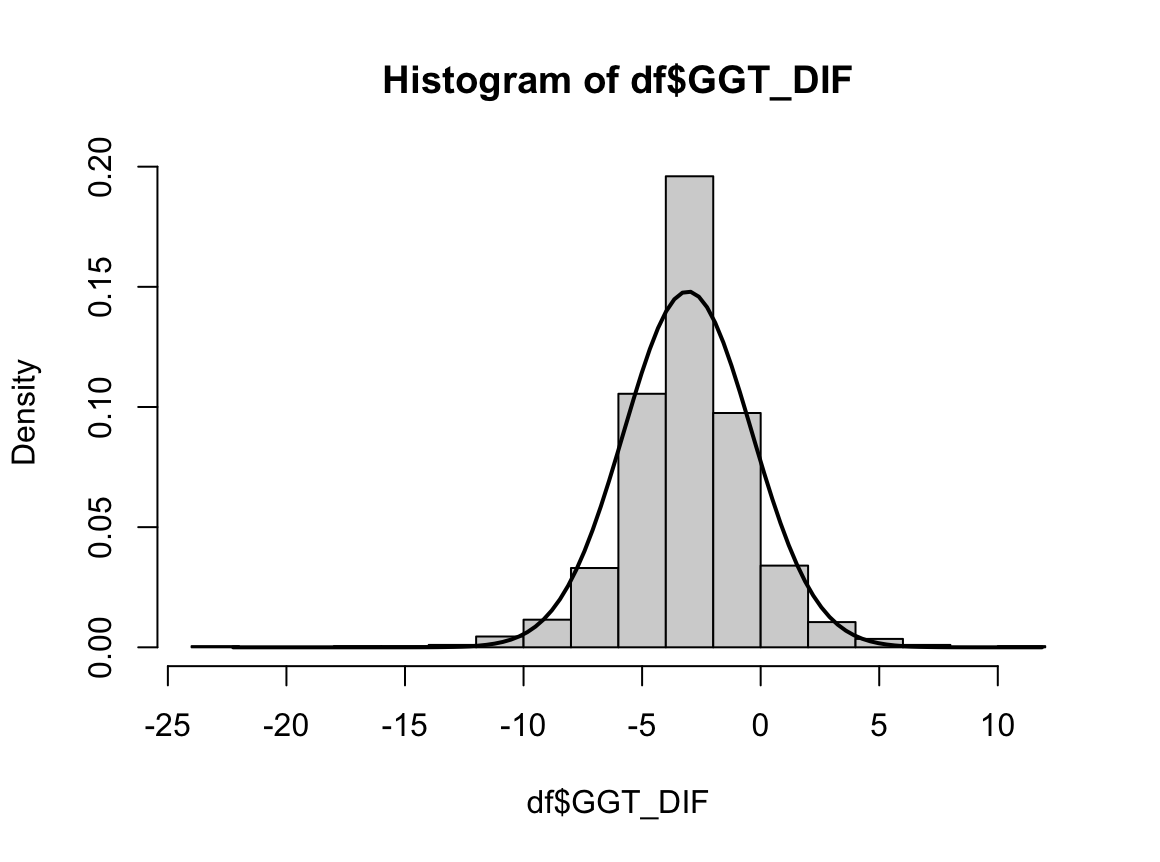
N수가 2,000개 미만이므로 Shapiro-Wilk 통계량의 p-value를 보면 0.05 이하이며, Q-Q Plot은 대부분의 데이터가 선상에 있지 않고, 히스토그램에서도 정규성을 따르지 않는 것처럼 보인다. 따라서 일표본 T검정 (One-sample T-test)를 시행할 수 없고, 일표본 윌콕슨 부호 순위 검정 (One-Sample Wilcoxon Signed Rank Test)을 시행해야 한다.

일표본 윌콕슨 부호 순위 검정 (One-Sample Wilcoxon Signed Rank Test)

이번 일표본 윌콕슨 부호 순위 검정 (One-Sample Wilcoxon Signed Rank Test)의 귀무가설과 대립 가설은 다음과 같다. 

귀무 가설:$H_0=$ 모집단의 NP1_raw 중앙값은 55이다.

대립 가설:$H_1=$ 모집단의 중앙값은 55보다 크거나 작다. (양측 검정)

1) 분석(A) > 비모수검정(N) > 일표본(O)

2) 이때 나오는 창의 첫 페이지인 "목적"은 건들지 않는다.

3) "필드"를 누르고 분석하고자 하는 NP1_raw를 오른쪽으로 넘긴다.

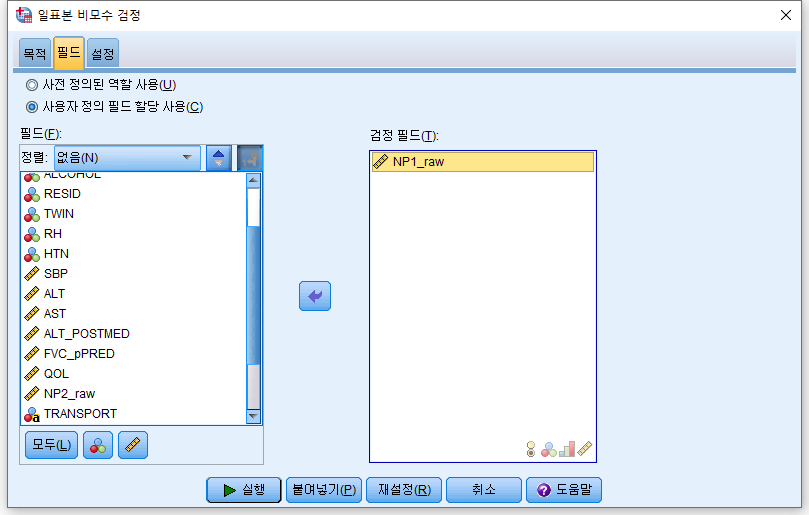
4) "사용자 정의에 의한 검정(T)"를 누르고 "평균과 가설값 비교(Wilcoxon 부호 순위 검정)"을 체크하고, 가설 중위수에는 검정하고자 하는 값인 55를 적는다. 그리고 "실행"을 누른다. 

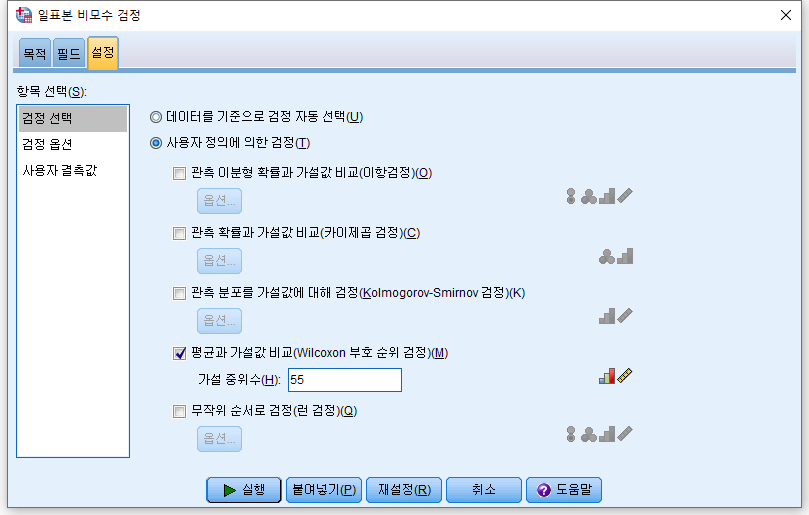
결과

p-value=0.000으로 이는 0.001보다 작다는 뜻이며, 0.05보다 작으므로 귀무가설을 기각하고 대립 가설을 받아들인다. 대립 가설은 중위수가 55가 아니라고 설정했었으므로 적어도 중위수가 55는 아니라고 이야기할 수 있다. 그렇다면 중위수가 얼마였길래 그럴까?

중위수 확인

1) 분석(A) > 기술통계량(E) > 데이터 탐색 (E)

2) 분석하고자 하는 변수인 NP1_raw을 "종속변수"에 넣어준다. 그 뒤 "확인"을 누른다.

결과

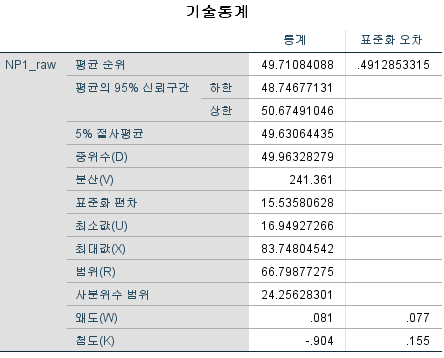
중위수는 49.96328279로 거의 50에 가깝다. 그렇다면 Wilcoxon 부호 순위 검정을 50에 대해 시행하면 어떻게 될까? 가설 중위수에 50을 넣고 실행을 눌러보자

결과

p-value>0.05이므로 귀무가설을 채택하여 50과 다르다고 할 수 없다는 결론을 얻는다. 

중요한 가정: 대칭성

위 논의에서 빠진 정말 중요한 가정이 하나 있다. 신경심리검사 1 원점수 (NP1_raw)의 분포가 어떤 점수를 기점으로 좌우대칭이라는 것이다. 윌콕슨 부호 순위 검정은 좌우대칭일 때 그 검정력이 극대화되며, 좌우대칭이 아니면 정확도가 떨어진다. 신경심리검사 1 원점수 (NP1_raw)의 분포를 히스토그램을 통해 알아보고자 하며 이는 위에 구해놓았다. 

봉우리가 세 개인 Trimodal shape을 하고 있고, 중앙값인 50을 기준으로 대칭인 것처럼 보인다. 따라서 위 분석에는 문제가 없는 듯하다.

가정이 성립하지 않는다면?

우리가 궁금하고, 문제가 되는 상황은 가정이 성립하지 않는 상황이다. 실제로 이럴 때가 많기 때문이다. 신경심리검사 2 원점수인 NP2_raw데이터의 분포를 확인해보자.

1) 분석(A) > 기술통계량(E) > 데이터 탐색 (E)

2) 분석하고자 하는 변수인 NP2_raw을 "종속변수"에 넣어준다. 그 뒤 "도표(T)..."를 선택한다.

3) "히스토그램(H)", "검정과 함께 정규성 도표(O)" 체크박스를 클릭하고 "계속(C)"를 누르고, 돌아가 "확인"을 누른다.

결과

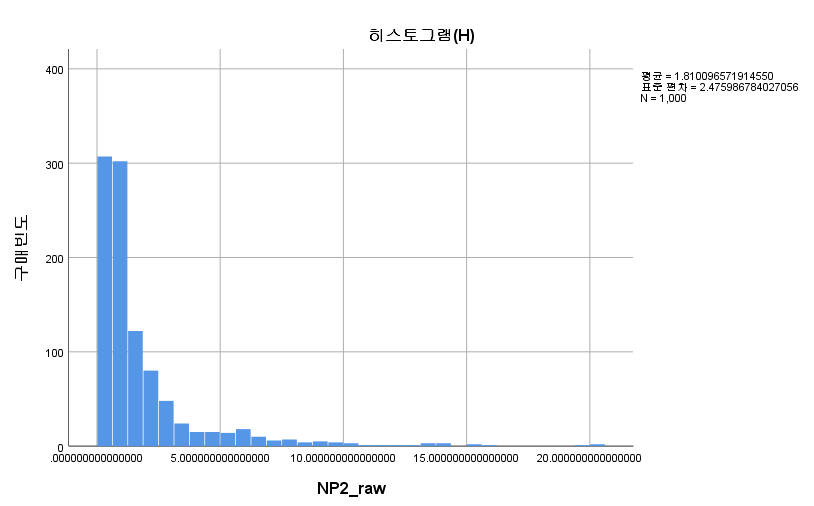
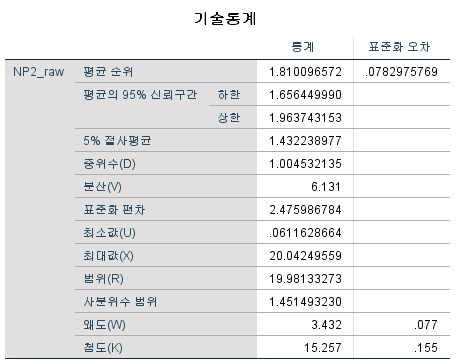
분포는 오른쪽으로 꼬리가 긴 right skewed 모양을 하고 있으며, 중위수는 1.004532153이다. 이 값에 대해 일표본 윌콕슨 부호 순위 검정을 해보자. 보통 우리는 "정규성을 만족하지 않으므로 윌콕슨 부호 순위 검정으로 모집단의 중위수를 검정하자."라고 생각한다. 만약 이런 논리에 따른다면 1.004532135에 대해 일표본 윌콕슨 부호 순위 검정을 시행한다면 당연히 유의하지 않은 결과가 나와야 한다. 

1) 분석(A) > 비모수검정(N) > 일표본(O)

2) 이때 나오는 창의 첫 페이지인 "목적"은 건들지 않는다.

3) "필드"를 누르고 분석하고자 하는 NP2_raw를 오른쪽으로 넘긴다.

4) "사용자 정의에 의한 검정(T)"를 누르고 "평균과 가설값 비교(Wilcoxon 부호 순위 검정)"을 체크하고, 가설 중위수에는 검정하고자 하는 값인 1.004532135를 적는다. 그리고 "실행"을 누른다. 

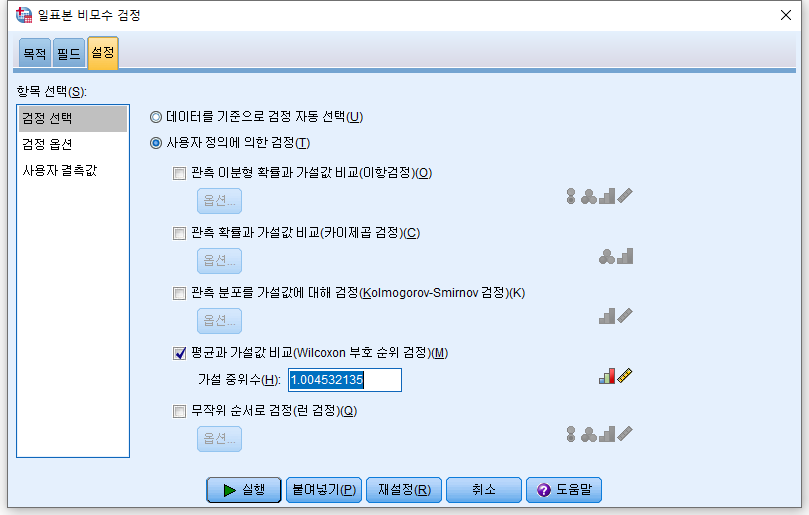
결과

p-value가 0.001보다도 작다는 결론에 도달한다. 참 중앙값으로 "NP2_raw의 중앙값이 참 중앙값과 같니?"라고 물어보았는데 "아니요"라고 대답하는 참사가 벌어진다. 이렇게 '잘못된' 결론을 내는 이유는 사실 우리가 윌콕슨 부호 순위 검정에 대해 '잘못된' 지식이자 선입견을 갖고 있기 때문이다. 윌콕슨 부호 순위 검정을 좌우 대칭인 데이터에만 사용할 수 있고, 그럴 때에만 중위수에 대한 검정을 의미한다. 이럴 때 선택할 수 있는 옵션이 많지 않긴 한데, 그중 하나는 변환 (transformation)이다. 이런 right skewed data는 로그 변환 (log-transformation)을 하면 대칭성이 갖추어지는 경우가 많다. 로그 변환을 하고 히스토그램을 그려 분포를 확인해보자. (로그 변환에 관한 글은 다음 링크에서 확인할 수 있다. 2022.11.30 - [통계 프로그램 사용 방법/SPSS] - [SPSS] 변수 계산 (산술 연산))

1) 변환(T) > 변수계산(C)

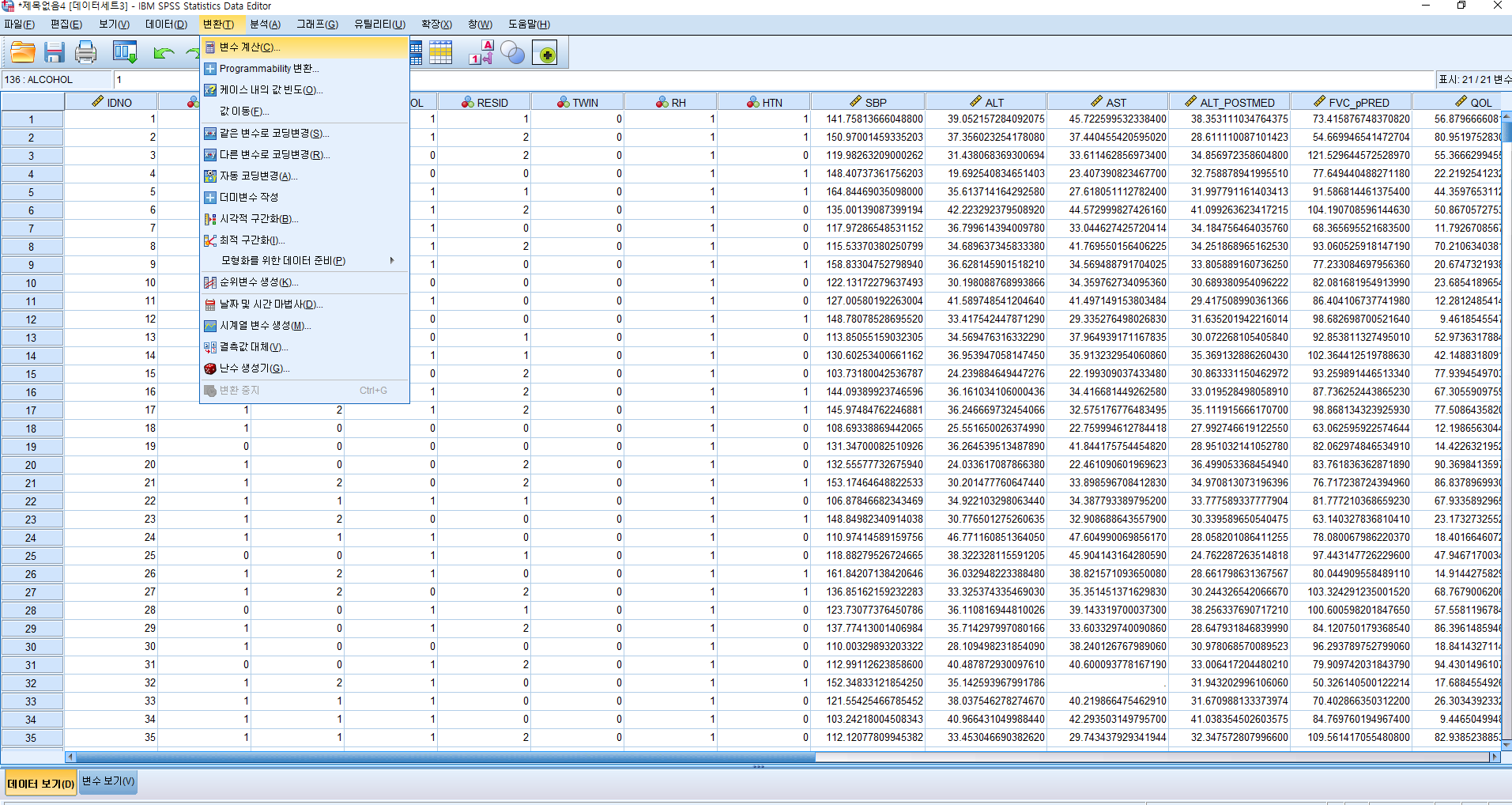
2) NP2_raw에 로그를 씌운 값을 log_NP2_raw라는 변수에 저장한다. 

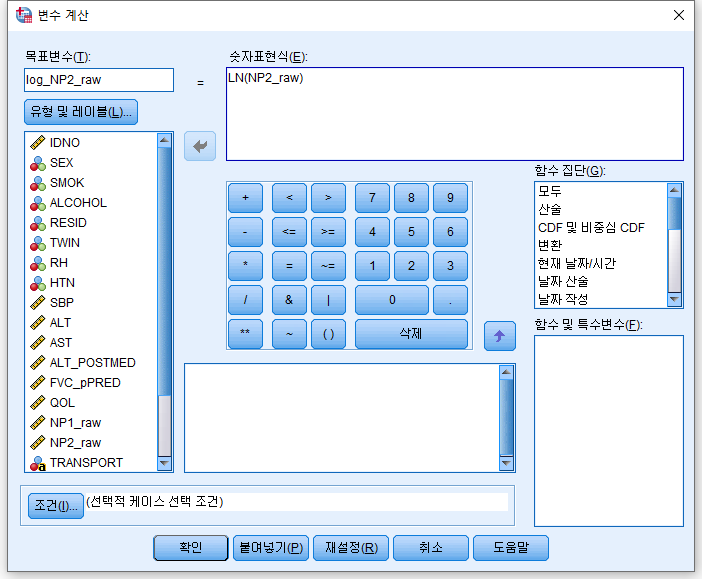
이렇게 변환한 변수가 대칭성을 띠는지, 혹시 정규성을 띠지는 않는지 (그러면 t-test를 시행하면 되므로) 확인한다.

1) 분석(A) > 기술통계량(E) > 데이터 탐색 (E)

2) 분석하고자 하는 변수인 NP2_raw을 "종속변수"에 넣어준다. 그 뒤 "도표(T)..."를 선택한다.

3) "히스토그램(H)", "검정과 함께 정규성 도표(O)" 체크박스를 클릭하고 "계속(C)"를 누르고, 돌아가 "확인"을 누른다.

결과

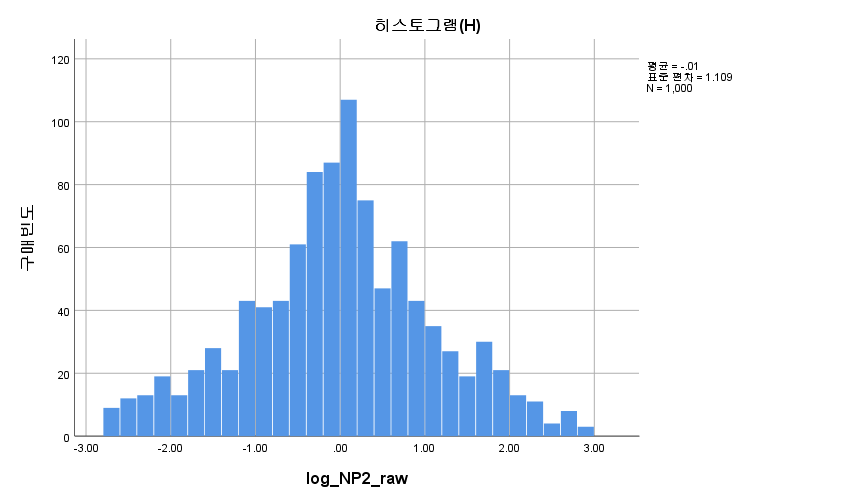
대칭성을 띠는 듯 하지만 정규성을 따르지는 않는다. 따라서 일표본 윌콕슨 부호 순위 검정을 시행하도록 한다.

1) 분석(A) > 비모수검정(N) > 일표본(O)

2) 이때 나오는 창의 첫 페이지인 "목적"은 건들지 않는다.

3) "필드"를 누르고 분석하고자 하는 NP2_raw를 오른쪽으로 넘긴다.

4) "사용자 정의에 의한 검정(T)"를 누르고 "평균과 가설값 비교(Wilcoxon 부호 순위 검정)"을 체크하고, 가설 중위수에는 검정하고자 하는 값을 넣는데, 원래 중위수가 1.004532135이었으므로 로그 변환을 하면 0과 가까우니 0을 적는다. 그리고 "실행"을 누른다. 

결과

이제야 유의하지 않다는 결론을 맞게 잘 내준다. 

그 외 다룰 내용 1: 정규성을 안 따르면 꼭 Wilcoxon test를 시행해야 하나?

 T-test의 전제조건은 표본 평균이 정규분포를 따르는 것이다. 그런데 중심 극한 정리에 따라 표본의 수 (우리 데이터에서는 n=1,000)가 커질수록 표본 평균의 분포는 정규성을 띠게 된다. 따라서 n수가 적당히 크기만 하면 표본이 정규분포를 따르는지와 관계없이 표본 평균은 정규성을 따른다고 할 수 있다. 이런 이유로 정규성과 관계없이 n수가 크기만 하면 t-test의 이용이 정당화되기도 한다. 합리적인 말이다.

 그런데 왜 정규분포를 따르는지 왜 다들 확인할까? 만약 모분포가 정규분포였다면 표본도 정규분포를 따를 확률이 높아진다. 물론 꼭 그런 건 아니지만 말이다. 따라서 표본이 정규분포를 따른다면, 모분포를 정규분포를 따른다고 할 수 있고, 그렇다면 n수가 작아도 표본 평균의 분포도 정규성을 따르니 t-test를 사용해도 되는 안전한 환경이 구축된다. 이런 이유로 정규성을 확인하게 된다.

그 외 다룰 내용 2: Wilcoxon signed rank test는 짝지어진 자료의 검정방법 아닌가?

 맞다. 하지만 one sample test에도 사용될 수 있다. 모수적 방법에서 대응 표본 T 검정 (paired T test)가 사실 일표본 T 검정 (One sample T test)와 같다는 것과 일맥상통하는 이야기다. (대응 표본 T검정은 다음 링크에서 확인할 수 있다.2022.11.30 - [반복 측정 자료 분석/SPSS] - [SPSS] 대응 표본 T검정 (Paired samples T-test))

[SPSS] 일표본 윌콕슨 부호 순위 검정 (비모수 일표본 중앙값 검정: One-Sample Wilcoxon Signed Rank Test) 정복 완료!

작성일: 2022.12.02.

최종 수정일: 2022.12.02.

이용 프로그램: IBM SPSS v26

운영체제: Windows 10

[R] 윌콕슨 부호 순위 검정 (비모수 짝지어진 표본 중앙값 검정: Wilcoxon signed rank test) - wilcox.test()

 짝지어진 두 분포의 평균이 다른지 확인하는 방법을 이전에는 대응 표본 T검정 (Paireed Sample T test)로 시행했었다. (2022.11.25 - [반복 측정 자료 분석/R] - [R] 대응 표본 T검정 (Paired samples T-test) - t.test()) 하지만 여기에는 중요한 가정이 필요한데, 두 변수의 차이가 정규분포를 이룬다는 것이다. 하지만 차이의 분포가 정규성을 따르지 않는다면 어떻게 해야 할까? 그럴 때 사용하는 것이 Wilcoxon signed rank test (윌콕슨 부호 순위 검정)이다.  

*실습용 데이터는 아래 링크를 클릭하면 다운로드할 수 있습니다.

2022.08.04 - [공지사항 및 소개] - 분석용 데이터 (update 22.12.01)

코드를 보여드리기에 앞서 워킹 디렉토리부터 지정하겠다.

워킹 디렉토리에 관한 설명은 다음 링크된 포스트에서 볼 수 있다.

2022.08.05 - [통계 프로그램 사용 방법/R] - [R] 작업 디렉토리 (Working Directory) 지정 - getwd(), setwd()

setwd("C:/Users/user/Documents/Tistory_blog")

데이터를 불러와 df에 객체로 저장하겠다.

데이터 불러오는 방법은 다음 링크에서 볼 수 있다.

2022.08.05 - [통계 프로그램 사용 방법/R] - [R] 데이터 불러오기 : EXCEL - read_excel(), read.xlsx()

2022.08.10 - [통계 프로그램 사용 방법/R] - [R] 데이터 저장하기 : CSV 파일 - write.csv(), write_csv()

2022.08.10 - [통계 프로그램 사용 방법/R] - [R] 데이터 불러오기 : SAS file (.sas7bdat) - read.sas7bdat(), read_sas()

install.packages("readr")
library("readr")
df<-read_csv("Data.csv")

목표: 모집단에서 GGT와 간기능 개선제 복용 후 GGT 중앙값에 차이가 있다고 할 수 있는가?

이번 포스팅의 목적은 1000명의 데이터를 가지고, 이 1000명이 기원한 모집단에서 GGT와 간 기능 개선제 복용 후 GGT의 중앙값에 차이가 있다고 할 수 있는지 판단하는 것이다.

전제: 정규성 검정 (차이)

 검정하고자 하는 두 변수의 차이가 정규성을 띤다면 paired t-test를 하면 되므로 정규성 여부를 파악하도록 한다. 따라서 GGT와 간 기능 개선제 복용 후 GGT(GGT_POSTMED)의 차이를 구하고 정규성 검정을 시행한다.

차이를 구하는 방법:

2022.11.25 - [통계 프로그램 사용 방법/R] - [R] 변수 계산 (산술 연산)

정규성 검정을 하는 방법:

2022.08.11 - [기술 통계/R] - [R] 정규성 검정 (1) : Q-Q plot - qqnorm(), qqline()

2022.08.11 - [기술 통계/R] - [R] 정규성 검정 (2) : 히스토그램 - hist(), dnorm()

2022.08.11 - [기술 통계/R] - [R] 정규성 검정 (3) : 정량적 검정 (Shapiro-Wilk, Kolmogorov-Smirnov) - shapiro.test(), ks.test()

2022.08.12 - [기술 통계/R] - [R] 정규성 검정 (4) : 정량적 검정 (Lilliefors test) - lillie.test()

2022.08.16 - [기술 통계/R] - [R] 고급 Q-Q Plot - Van der Waerden, Rankit, Tukey, Blom

코드

##GGT 차이 변수 만들기
df$GGT_DIF<-df$GGT-df$GGT_POSTMED

##GGT_DIF의 정규성 검정
# 1) Q-Q plot 그리기
qqnorm(df$GGT_DIF)
qqline(df$GGT_DIF)
# 2) 히스토그램 그리기
hist(df$GGT_DIF, prob=TRUE, breaks=20)
GGT_DIFrange<-seq(min(df$GGT_DIF),max(df$GGT_DIF),length=max(max(df$GGT_DIF)-min(df$GGT_DIF),100))
ND<-dnorm(GGT_DIFrange,mean=mean(df$GGT_DIF),sd=sd(df$GGT_DIF))
lines(GGT_DIFrange, ND, lwd=2)
# 3) Shapiro-Wilk test 시행하기
shapiro.test(df$GGT_DIF)

결과

	Shapiro-Wilk normality test

data:  df$GGT_DIF
W = 0.94868, p-value < 2.2e-16

 N수가 2,000개 미만이므로 Shapiro-Wilk 통계량의 p-value를 보면 0.05 이하이며, Q-Q Plot은 대부분의 데이터가 선상에 있지 않다. 히스토그램에서는 정규성을 따르는 것처럼 보이지만 이는 개인의 느낌이므로 정확한 것은 아니다. 따라서 대응 표본 T검정 (Paired sample T-test)를 시행할 수 없고, 윌콕슨 부호 순위 검정 (Wilcoxon Signed Rank Test)을 시행해야 한다.

윌콕슨 부호 순위 검정 (Wilcoxon Signed Rank Test) 코드

wilcox.test(df$GGT, df$GGT_POSTMED, correct=FALSE, paired=TRUE)

wilcox.test(df$GGT, df$GGT_POSTMED, correct=FALSE, paired=TRUE) : df데이터의 GGT변수와 df데이터의 GGT_POSTMED로 검정을 하는데, 연속성 수정은 하지 말고 (correct=FALSE), 대응표본이니까 (paired=TRUE) 윌콕슨 부호 순위 검정을 시행하라. (연속성 수정은 다음 글을 참고하길 바란다.2022.08.30 - [통계 이론] - [이론] 연속성을 수정한 카이 제곱 검정 (Chi-squared test with Yates's correction for continuity))

결과

	Wilcoxon signed rank test

data:  df$GGT and df$GGT_POSTMED
V = 22907, p-value < 2.2e-16
alternative hypothesis: true location shift is not equal to 0

Wilcoxon signed rank test

data:  df$GGT and df$GGT_POSTMED

V = 22907, p-value < 2.2e-16

alternative hypothesis: true location shift is not equal to 0

중요한 건 p-value다. p-value가 0.05보다 작으므로 df의 GGT와 GGT_POSTMED는 차이가 있다고 할 수 있다. 지난번 일표본 윌콕슨 부호 순위 검정에서도 밝혔듯이 윌콕슨 부호 순위 검정은 가정이 필요 없는 검정이 아니다. 대칭이라는 가정이 필요하다.(2022.11.29 - [모평균 검정/R] - [R] 일표본 윌콕슨 부호 순위 검정 (비모수 일표본 중앙값 검정: One-Sample Wilcoxon Signed Rank Test) - wilcox.test()) 따라서 대칭여부를 확인해야 하는데, 위 GGT_DIF의 히스토그램을 보면 좌우대칭임을 확인할 수 있다. 따라서 원 결론 그대로 차이가 난다고 결론을 내리면 된다.

 그런데, 눈치를 챈 독자도 있겠지만, 비모수 일표본 검정도, 대응 표본 검정도 모두 윌콕슨 부호 순위 검정을 실시한다. 이는 모수적인 방법에서 대응 표본 T 검정 (paired T test)가 사실 일표본 T 검정 (One sample T test)와 같다는 것과 일맥상통하는 이야기다. 이 말을 비틀어 생각하면, 일표본 윌콕슨 부호 순위 검정으로 대응표본 윌콕슨 부호 순위 검정을 시행할 수 있다는 말이다. 즉 위에서 만들 DDT_DIF변수로 0에 대해 일표본 윌콕슨 부호 순위 검정을 시행하면 같은 결과를 내는 것을 확인할 수 있다.

코드

wilcox.test(df$GGT_DIF, mu=0, correct=FALSE)

결과

	Wilcoxon signed rank test

data:  df$GGT_DIF
V = 22907, p-value < 2.2e-16
alternative hypothesis: true location is not equal to 0

코드 정리

##워킹 디렉토리 지정
setwd("C:/Users/user/Documents/Tistory_blog")

##데이터 불러오기
install.packages("readr")
library("readr")
df<-read_csv("Data.csv")


##GGT 차이 변수 만들기
df$GGT_DIF<-df$GGT-df$GGT_POSTMED


##GGT_DIF의 정규성 검정
# 1) Q-Q plot 그리기
qqnorm(df$GGT_DIF)
qqline(df$GGT_DIF)
# 2) 히스토그램 그리기
hist(df$GGT_DIF, prob=TRUE, breaks=20)
GGT_DIFrange<-seq(min(df$GGT_DIF),max(df$GGT_DIF),length=max(max(df$GGT_DIF)-min(df$GGT_DIF),100))
ND<-dnorm(GGT_DIFrange,mean=mean(df$GGT_DIF),sd=sd(df$GGT_DIF))
lines(GGT_DIFrange, ND, lwd=2)
# 3) Shapiro-Wilk test 시행하기
shapiro.test(df$GGT_DIF)


##윌콕슨 부호 순위 검정 시행하기
wilcox.test(df$GGT, df$GGT_POSTMED, correct=FALSE, paired=TRUE)


##일표본 윌콕슨 부호 순위 검정 시행하기
wilcox.test(df$GGT_DIF, mu=0, correct=FALSE)

[R] 윌콕슨 부호 순위 검정 (비모수 짝지어진 표본 중앙값 검정: Wilcoxon signed rank test) 정복 완료!

작성일: 2022.12.01.

최종 수정일: 2022.12.06.

이용 프로그램: R 4.2.2

RStudio v2022.07.2

RStudio 2022.07.2+576 "Spotted Wakerobin" Release

운영체제: Windows 10, Mac OS 12.6.1