의학 통계 코드 저장소

[이론] 피셔 정확 검정 (Fisher's exact test)

 범주형 자료의 통계 분석을 진행하다 보면 반드시 만나게 되는 검정이 피셔 정확 검정이다. 피셔 정확 검정은 단순히 초기하 분포의 확률을 구하는 것이다. 이해할 수 있는 언어로 표현하면 다음과 같다.

초기하 분포 (Hypergeometric distritubion)

 먼저 초기하 분포를 이해해야 한다. 

상황: 10개의 공이 들어있는 주머니가 있다. 그중 7개는 파란색, 3개는 빨간색이다. 

전제: 특정 색깔의 공이 더 잘 뽑히는 것은 아니다. 어떤 색이 뽑힐지는 랜덤이다. (=뽑는 사람은 공을 보지 않고서는 색을 알 수 없다 = 독립이다.)

문제: 5개의 공을 꺼냈는데, 3개가 파란색, 2개가 빨간색일 확률은 얼마인가?

답: 

$$\frac{_{7}C_{3}\times _{3}C_{2}}{_{10}C_{5}} = \frac{\begin{pmatrix} 7 \\  3 \end{pmatrix} \times \begin{pmatrix} 3 \\  2 \end{pmatrix}} {\begin{pmatrix} 10 \\  5 \end{pmatrix}}$$

해설: 

분모에는 10개 공 중에서 5개를 고르는 경우의 수인 $_{10}C_{5}$을 넣는다.

분자에는 파란 공 7개 중 3개를 고르는 경우의 수인 $_{7}C_{3}$과 빨간 공 3개 중 2개를 고르는 $_{3}C_{2}$를 곱한다.

즉, $N$개 중 $n$개를 고르는데, 음이 아닌 어떤 정수 $k$에 대해, $k$개는 $K$중에서, $n-k$개는 $N-K$개에서 고르는 경우에 대해 논하는 것이 초기하 분포다. 그리고 확률 밀도 함수(discrete density function, 혹은 probability mass function)는 다음과 같이 기술된다.

$$f_{k} (k;K,N,n)=\frac{_{K}C_{k}\times _{N-K}C_{n-k}}{_{N}C_{n}} = \frac{\begin{pmatrix} K \\  k \end{pmatrix} \times \begin{pmatrix} N-K \\  n-k \end{pmatrix}} {\begin{pmatrix} N \\  n \end{pmatrix}}$$

 말이 어려워 보일지 몰라도 위 문제에 대한 해설을 일반화한 것뿐이다.

피셔 정확 검정 (Fisher's exact test)은 어떻게 하는 건데?

피셔 정확 검정 결과를 직접 손으로 계산해보고자 한다.

성별과 RH 혈액형 분포가 다음과 같다고 하자.

다음 두 가지를 유의하며 읽어야 한다.

1) 먼저, 카이 제곱 검정 때와 마찬가지로 합계에 있는 파란색 숫자들은 변하지 않는 고정값으로 볼 것이다.

2) 우리는 빨간색 숫자인 여성이면서 RH-인 사람의 수에 집중할 것이다.

 여성은 482명, RH-는 6명이므로 빨간색 숫자가 있는 칸에는 이론적으로 0부터 6(482와 6중 작은 숫자)까지의 숫자가 들어갈 수 있다. 만약 0이라면, RH- 6명 중 전원이 남성인 것이므로 "남성에 RH-가 많다."라고 이야기할 수도 있을 것이다. 반대로 6이라면 RH- 6명 중 전원이 여성이므로 "여성에 RH-가 많다."라고 이야기할 수도 있을 것이다.

 본 글의 최종 목적이 되는 양측 검정 (two-sided, two-tailed) 귀무가설은 "성별과 RH 혈액형은 관련성이 없다."이므로 빨간색 숫자가 있는 칸에 들어가는 숫자가 작아서 0에 가까워지거나 커서 6에 가까워지는 상황에서는 p-value가 작아지도록 통계량이 설계되어야 한다. 

 위에서 공부한 초기하 분포의 확률을 본 상황에 대입하면 다음과 같다.

전제되는 상황: 특정 성별이 특정 RH 혈액형을 가질 가능성이 더 높지 않다. 즉 독립적이다.

"총 인원 1,000명 중 RH- 6명을 고를 건데, 1명은 여성 482명 중에서, 나머지 5명은 남성 518명 중에서 고를 것이다. 그렇게 계산될 확률은 얼마인가?"

초기하 분포의 확률 공식을 사용하여 위 문제의 답은 다음과 같이 구할 수 있다.

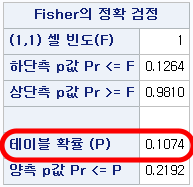
$$ \frac{\begin{pmatrix} 482 \\  1 \end{pmatrix} \times \begin{pmatrix} 518 \\  5 \end{pmatrix}} {\begin{pmatrix} 1000 \\  6 \end{pmatrix}}=0.10739...$$

이 값이 SAS 결과에서는 "테이블 확률(P)"로 제시된다. 본 테이블이 계산될 확률을 의미한다. 

사실 피셔 정확 검정에서는 여러 대립 가설이 있을 수 있다. 각 상황에 따라 피셔 정확 검정의 결과를 계산해보고자 한다.

대립 가설 1) 여성일수록 RH-일 가능성이 높아지는 관련성이 있다.  (One-sided, One-Tailed)

 그렇다면 우리가 구하고자 하는 p-value의 의미는 다음과 같다.

"성별과 RH 혈액형 사이에는 관련성이 없다는 것이 진실인데 여성일수록 RH-일 가능성이 높아지는 관련성이 있다고 결론을 내릴 확률"

우리 데이터를 보면 RH-인 6명 중 5명이 남성에 쏠려있으므로 이 상황에서 구해지는 p-value는 높은 값을 갖는 것이 합리적이다. 그리고 그 계산은 다음 확률을 모두 더해서 계산한다.

 (1) 여성이면서 RH-인 사람이 1명일 확률 :$ \frac{\begin{pmatrix} 482 \\  1 \end{pmatrix} \times \begin{pmatrix} 518 \\  5 \end{pmatrix}} {\begin{pmatrix} 1000 \\  6 \end{pmatrix}}$

 (2) 여성이면서 RH-인 사람이 2명일 확률 :$ \frac{\begin{pmatrix} 482 \\  2 \end{pmatrix} \times \begin{pmatrix} 518 \\  4 \end{pmatrix}} {\begin{pmatrix} 1000 \\  6 \end{pmatrix}}$

 (3) 여성이면서 RH-인 사람이 3명일 확률 :$ \frac{\begin{pmatrix} 482 \\  3 \end{pmatrix} \times \begin{pmatrix} 518 \\  3 \end{pmatrix}} {\begin{pmatrix} 1000 \\  6 \end{pmatrix}}$

 (4) 여성이면서 RH-인 사람이 4명일 확률 :$ \frac{\begin{pmatrix} 482 \\  4\end{pmatrix} \times \begin{pmatrix} 518 \\  2 \end{pmatrix}} {\begin{pmatrix} 1000 \\  6 \end{pmatrix}}$

 (5) 여성이면서 RH-인 사람이 5명일 확률 :$ \frac{\begin{pmatrix} 482 \\  5 \end{pmatrix} \times \begin{pmatrix} 518 \\  1 \end{pmatrix}} {\begin{pmatrix} 1000 \\  6 \end{pmatrix}}$

 (6) 여성이면서 RH-인 사람이 6명일 확률 :$ \frac{\begin{pmatrix} 482 \\  6 \end{pmatrix} \times \begin{pmatrix} 518 \\  0 \end{pmatrix}} {\begin{pmatrix} 1000 \\  6 \end{pmatrix}}$

이 값을 모두 더하면, 즉 $$\sum_{k=1}^{6} { \frac{\begin{pmatrix} 482 \\  k \end{pmatrix} \times \begin{pmatrix} 518 \\  6-k \end{pmatrix}} {\begin{pmatrix} 1000 \\  6 \end{pmatrix}}}=0.98085...$$

가 되어 SAS 결과에서의 "상단측 p값 Pr>=F"값이 산출된다. 

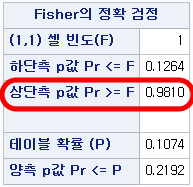
(1) 여성이면서 RH-인 사람의 수는 1이다. 이를 F라 칭한다.

(2) 여성이면서 RH-인 사람의 수가 F 이상인 확률들의 총합을 "상단측 p값 Pr>=F"라고 한다.

만약 유의성의 기준 ($\alpha$)이 0.3였다면 다음과 같이 해석된다.

성별과 RH혈액형 사이에 관련성이 없다는 것이 진실이라고 가정하자. 이때 RH- 환자 6명 중 한 명 이상이 여성일 확률은 0.9810다. 이건 0.3보다도 높으므로 현실적으로 일어날 수 있는 일이다. 따라서 여성일수록 RH- 혈액형을 가질 것이라고는 할 수 없다고 결론지어진다.

대립 가설 2) 여성일수록 RH-일 가능성이 낮아지는 관련성이 있다.  (One-sided, One-Tailed)

 그렇다면 우리가 구하고자 하는 p-value의 의미는 다음과 같다.

"성별과 RH 혈액형 사이에는 관련성이 없다는 것이 진실인데 여성일수록 RH-일 가능성이 낮아지는 관련성이 있다고 결론을 내릴 확률"

우리 데이터를 보면 RH-인 6명 중 1명만이 여성이므로 이 상황에서 구해지는 p-value는 상대적으로 낮은 값을 갖는 것이 합리적이다. 그리고 그 계산은 다음 확률을 모두 더해서 계산한다.

 (1) 여성이면서 RH-인 사람이 0명일 확률 :$ \frac{\begin{pmatrix} 482 \\  0 \end{pmatrix} \times \begin{pmatrix} 518 \\  6 \end{pmatrix}} {\begin{pmatrix} 1000 \\  6 \end{pmatrix}}$

 (2) 여성이면서 RH-인 사람이 1명일 확률 :$ \frac{\begin{pmatrix} 482 \\  1 \end{pmatrix} \times \begin{pmatrix} 518 \\  5 \end{pmatrix}} {\begin{pmatrix} 1000 \\  6 \end{pmatrix}}$

이 값을 모두 더하면, 즉 $$\sum_{k=0}^{1} { \frac{\begin{pmatrix} 482 \\  k \end{pmatrix} \times \begin{pmatrix} 518 \\  6-k \end{pmatrix}} {\begin{pmatrix} 1000 \\  6 \end{pmatrix}}}=0.12644...$$

가 되어 SAS 결과에서의 "하단측 p값 Pr>=F"값이 산출된다.

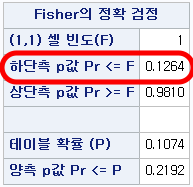
(1) 여성이면서 RH-인 사람의 수는 1이다. 이를 F라 칭한다.

(2) 여성이면서 RH-인 사람의 수가 F 이하인 확률들의 총합을 "하단측 p값 Pr<=F"라고 한다.

만약 유의성의 기준 ($\alpha$)이 0.3였다면 다음과 같이 해석된다.

성별과 RH혈액형 사이에 관련성이 없다는 것이 진실이라고 가정하자. 이때 RH- 환자 6명 중 한 명 이하만이 여성일 확률은 0.1264다. 이 값은 0.3보다도 낮으므로 이렇게 적은 숫자의 여성이 RH-혈액형을 갖는 것은 현실적으로 일어나기 어려운 일이다. 그러므로 성별과 RH혈액형 사이에 관련성이 없다고 봤던 가정에 문제가 있다고 할 수 있다. 따라서 차라리 여성일수록 RH-혈액형일 가능성이 떨어진다고 보는 것이 합리적이다. 

즉 사고의 흐름은 다음과 같다.

"RH-인 사람 중 여성이 1명밖에 안되네?"

$\rightarrow$ "1명 혹은 0명 밖에 없다는 것은 여성일수록 RH-일 가능성이 떨어진다는 것 아닐까?"

$\rightarrow$  [가정] "성별이랑 RH혈액형 간에 아무런 관계가 없다고 가정해보자."

$\rightarrow$ "그때 RH-중 1명 혹은 0명만이 여성일 확률이 얼마라고? 0.1264라고."

$\rightarrow$ "이게 현실적으로 일어나기는 어려운 일 아니야?"

$\rightarrow$ "그러면 차라리 여성일수록 RH-일 확률이 높은 게 진실이고 그런 현실 속에서 발생한 일이라고 보는 게 낫겠다."

대립 가설 3) 성별과 RH 혈액형 사이에는 모종의 관련성이 있다.  (Two-sided, Two-Tailed)

 그렇다면 우리가 구하고자 하는 p-value의 의미는 다음과 같다.

"성별과 RH 혈액형 사이에는 관련성이 없다는 것이 진실인데 여성일수록 RH-일 가능성이 높아지거나 낮아지는 관련성이 있다고 결론을 내릴 확률"

 모종의 관련성이 있다면 여성이면서 RH-인 사람의 수는 극도로 작아지거나 커질 것이다. 여기에서는 그 수가 1이다. 1이 될 확률은 위에서 0.1074로 산출이 되었다. 그 확률보다 작은 경우는 여성이면서 RH-인 사람의 수가 1보다 적거나, 6에 가까운 경우일 뿐일 것이다. 그 확률들의 총합이 피셔 정확 검정의 양측 검정 p-value이다. 

Yes에 해당하는 사람들의 확률을 모두 더하면 $0.21917$이 계산되며 이는 SAS 결과에서의 "양측 p값 Pr>=P"와 같다. 또한, 이 값이 보통 논문에서 사용되는 피셔 정확 검정의 값이다.

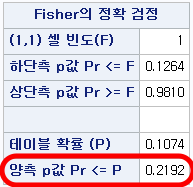
만약 유의성의 기준 ($\alpha$)이 0.3였다면 다음과 같이 해석된다.

성별과 RH혈액형 사이에 관련성이 없다는 것이 진실이라고 가정하자. 이때 RH- 환자 6명 중 한 명만이 여성일 확률은 0.1074다. 이 확률보다 일어나기 어려운 현상은 RH-인 여성이 0명인 상황, 5명인 상황, 6명인 상황이다. 이런 일들이 일어날 확률은 0.2192다. 이건 0.3보다도 낮으므로 현실적으로 일어나기 어렵다. 즉, 성별과 RH혈액형 사이에 관련성이 없다고 봤던 가정에 문제가 있다고 할 수 있다. 따라서 차라리 여성일수록 RH-혈액형일 가능성이 높아지거나 낮아지는 것이 진실이라고 보는 것이 합리적이다. 

세 가지 p-value 중 어떤 값을 써야 하는가?

피셔 정확 검정의 p-value는 아무 거나 쓰는 것이 아니다. 어떤 대립 가설을 사용하는지에 따라 크게 달라진다.

1) 상단측 p값 Pr>=F : 분할표의 대각선에 많은 데이터가 몰릴 것으로 예상될 때 사용한다. 만약 변수가 순서형 변수라면 크기순으로 행과 열을 채우니 일반적으로 양의 상관관계가 예상될 때 사용한다고 할 수 있다.

2) 하단측 p값 Pr<=F : 분할표의 대각선에 외의 셀에 많은 데이터가 몰릴 것으로 예상될 때 사용한다. 만약 변수가 순서형 변수라면 크기순으로 행과 열을 채우니 일반적으로 음의 상관관계가 예상될 때 사용한다고 할 수 있다.

3) 양측 p값 Pr<=P : 대립 가설이 없을 때 사용한다. 즉, 어느 방향으로든 관련성이 있는지 보고자 할 때 사용하는 값이다.

[이론] 피셔 정확 검정 (Fisher's exact test) 정복 완료!

작성일: 2022.08.26.

최종 수정일: 2022.08.27.

이용 프로그램: SAS v9.4

운영체제: Windows 10

[이론] 카이 제곱 검정 (Chi-squared test)

 범주형 자료의 분포에 유의미한 차이가 있는지 검정하기 위해 카이 제곱 검정 (Chi-squared test)를 시행하곤 한다. 깊은 이야기를 하기 전에 이번 글에서는 카이 제곱 검정 계산이 실제로 어떻게 시행되고, 자유도의 개념이 왜 존재하는지에 대해 다뤄보고자 한다.

 어떤 동네의 주민 1,000명의 흡연 여부, 폐암 여부에 따른 분포(관찰 빈도)가 다음과 같다고 하자. 

이 표를 보고 폐암 환자가 더 많다고 할 수 있는지에 대한 검정이 카이 제곱 검정이다. 카이 제곱 검정을 하는 과정은 다음과 같다.

1) 기대 빈도 산출

2) 카이 제곱 검정량 산출

3) 자유도 산출

4) p-value 계산

1) 기대 빈도 산출

카이 제곱 검정의 시작점은 "총합"이 정해져 있다고 하는데서부터 시작한다. 

 폐암 환자는 200명, 정상인은 800명, 흡연자는 300명, 비흡연자는 700명이라는 사실은 변하지 않는다고 생각하는 것이다. 이때 흡연자이자 폐암 환자인 사람은 몇 명이라고 예상하는 것이 합당할까? 다시 말하면, 흡연과 폐암이 아무 관련성이 없다면 (A)에는 몇 명이 있다고 예측하는 것이 합리적일까?

 폐암 환자는 200명이다. 또한 전체 인구 중 흡연자는 30%를 차지한다 (1,000명 중 300명). 따라서 200명의 30%인 60명이 흡연자가 될 것이라고 생각할 수 있다.  이런 식으로 기대 빈도 표를 모두 채우면 다음과 같다.

2) 카이 제곱 검정량 산출

관찰 빈도에서 기대 빈도 값을 뺀다.

각 값을 제곱한다.

각 값을 기대 빈도로 나눈다.

네 개의 값을 모두 더하면 카이 제곱 통계량이 된다.

$$카이 제곱 검정량=\frac{\left(75-60\right)^{2}}{60}+\frac{\left(225-240\right)^{2}}{240}+\frac{\left(125-140\right)^{2}}{140}+\frac{\left(6575-560\right)^{2}}{560}=6.6964$$

이 값을 잘 생각해보면, 관찰 빈도와 기대 빈도의 차이가 클수록 카이 제곱 검정량이 커진다는 것을 알 수 있다. 즉, 아무 관련성이 없다고 가정했을 때 예상되는 기대 빈도보다 더 많은 양이 관찰되거나, 훨씬 적은 양이 관찰된다면 카이 제곱 검정량이 커진다는 것이다. 따라서 너무나도 당연한 소리지만, 카이 제곱 검정량이 클수록 예상하지 못했던 결과라는 뜻이고, 유의미한 관련성이 있다는 뜻이다. 

 (따라서, 카이 제곱 검정량이 클수록 p-value가 작아지는 방식의 디자인이 필요하다.)

3) 자유도 산출

$$자유도=\left(열의\ 개수 - 1 \right)\times\left(행의\ 개수 - 1 \right)=1$$

4) p-value 계산

다음 두 가지 과정을 생각해보도록 한다.

 1) ɑ=0.05로 하였을 때 유의미한 관련성이 있다고 할 수 있는가?

자유도가 1인 카이 제곱 분포에서 카이 제곱 검정량이 0~3.84 사이일 때 적분 값이 0.95다. 즉, 아래 그림에서 빨간색 영역의 면적이 0.95, 파란색 영역의 면적이 0.05다. 따라서, 자유도가 1일 때, 카이 제곱 검정량이 0에서 3.84 사이로 관찰될 확률은 95%라는 뜻이고, 동시에 3.84 이상 관찰될 확률은 5%라는 뜻이다. 그러므로, 산출된 카이 제곱 검정량이 3.84보다 크면 유의미한 관련성이 있다는 것인데, 위 폐암-흡연의 카이 제곱 검정량은 6.6964였으므로 유의미한 관련성이 있다고 결론 내릴 수 있다.

[R] 위 그림 코드

x<-seq(0,10,0.001)
y<-dchisq(x,1)
plot(x,y,type="l",ann=FALSE, ylim=c(0,0.5))
title(main="Chi-Squared Distribution")
xrange<-seq(0,3.841458821,0.01)
funx<-dchisq(xrange,1)
polyx<-c(xrange,rev(xrange))
polyy<-c(rep(0,length(funx)),rev(funx))
polygon(polyx,polyy,col=2,border=NA)

xrange2<-seq(3.841458821,10,0.01)
funx2<-dchisq(xrange2,1)
polyx2<-c(xrange2,rev(xrange2))
polyy2<-c(rep(0,length(funx2)),rev(funx2))
polygon(polyx2,polyy2,col=4,border=NA)

2) 그래서 p-value가 몇인데?

0부터 산출된 카이 제곱 검정량인 6.6964까지의 자유도가 1인 카이 제곱 함수의 적분 값(아래 그림 초록색 영역)은 0.9903394이다. 따라서 p-value는 1에서 초록색 영역 넓이를 뺀 0.0097 (아래 그림 보라색 영역)이다. 즉, p-value는 산출된 카이 제곱 검정량에서부터의 카이 제곱 함수의 적분 값을 의미한다.

[R] 위 그림 코드

x<-seq(0,10,0.001)
y<-dchisq(x,1)
plot(x,y,type="l",ann=FALSE, ylim=c(0,0.5))
title(main="Chi-Squared Distribution")
xrange<-seq(0,6.696428571,0.01)
funx<-dchisq(xrange,1)
polyx<-c(xrange,rev(xrange))
polyy<-c(rep(0,length(funx)),rev(funx))
polygon(polyx,polyy,col=3,border=NA)

xrange2<-seq(6.696428571,10,0.01)
funx2<-dchisq(xrange2,1)
polyx2<-c(xrange2,rev(xrange2))
polyy2<-c(rep(0,length(funx2)),rev(funx2))
polygon(polyx2,polyy2,col=6,border=NA)

[R] p-value 산출 코드

1-pchisq(6.696428571,1)

그렇다면 카이 제곱 분포란 무엇인가?

카이 제곱 분포란 제곱한 정규분포의 합을 의미한다. 제곱한 정규분포를 여러 개 더할 수 있는데, 몇 개를 더했느냐가 자유도다.

$k$가 자유도, $Z$가 정규분포라면 카이 제곱 분포 $Q$는 다음과 같이 표현된다.

$$Q=\sum_{n=1}^k Z_{i}^{2}$$

이해할 수 있는 언어로 설명하기 위해 $k=1$인 상황을 가정하여 설명해 보겠다.

$$Q= Z^{2}$$

우리가 익히 알고 있는 정규분포에서 95%를 나타내는 범주는 [-1.96, 1.96]이다. 즉, 아래 그림에서 노란색 영역의 넓이는 0.95다.

[R] 위 그림 코드

x<-seq(-4,4,0.001)
y<-dnorm(x)
plot(x,y,type="l",ann=FALSE)
title(main="Normal Distribution")
xrange<-seq(-1.959964,1.959964,0.01)
funx<-dnorm(xrange)
polyx<-c(xrange,rev(xrange))
polyy<-c(rep(0,length(funx)),rev(funx))
polygon(polyx,polyy,col=7,border=NA)

카이 제곱은 정규분포를 제곱한다고 하였다. 

0은 0으로,

1은 1로,

2는 4로,

3은 9로, 

4는 16으로 이동한다.

음의 영역에서도

-1은 1로,

-2는 4로,

-3은 9로,

-4는 16으로 이동한다. 

즉 $x=0$이라는 직선을 기준으로 그래프를 반으로 접은 뒤에 양옆으로 잡아당긴 형태가 된다.

따라서 카이 제곱 분포의 그래프는 음의 영역이 존재하지 않는다.

그러면 위 그림의 노란색 영역은 어떻게 변할까?

1.96의 제곱도 3.84, -1.96의 제곱도 3.84이다.

[R] 위 그림 코드

x<-seq(-1.959964,1.959964,0.001)
y<-x^2
plot(x,y,type="l",ann=FALSE,xlim=c(-2,2),ylim=c(0,4))
par(new=TRUE)
x<-seq(-3,3,0.001)
y<-x*0+3.841458821
plot(x,y,type="l",col="red",ann=FALSE,xlim=c(-2,2),ylim=c(0,4))
par(new=TRUE)
y<-seq(-3,3.841458821,0.001)
x<-y*0-1.959964
plot(x,y,type="l",col="blue",ann=FALSE,xlim=c(-2,2),ylim=c(0,4))
par(new=TRUE)
y<-seq(-3,3.841458821,0.001)
x<-y*0+1.959964
plot(x,y,type="l",col="blue",ann=FALSE,xlim=c(-2,2),ylim=c(0,4))

따라서, 0에서 3.84까지 적분한 값이 0.95가 되는 아래와 같은 그래프일 것이다.

[R] 위 그림 코드

x<-seq(0,5,0.001)
y<-dchisq(x,1)
plot(x,y,type="l",ann=FALSE, ylim=c(0,0.5))
title(main="Chi-Squared Distribution")
xrange<-seq(0,3.841458821,0.01)
funx<-dchisq(xrange,1)
polyx<-c(xrange,rev(xrange))
polyy<-c(rep(0,length(funx)),rev(funx))
polygon(polyx,polyy,col=7,border=NA)

따라서, 일반적인 양수에 대해 다음의 두 등식이 성립한다.

[1] pnorm(a)=0.5*pchisq(a^2,1)+0.5
[2] pnorm(-a)+0.5*pchisq(a^2,1)+0.5=1

그런데 자유도는 왜 존재하는 개념인가?

우리는 위에서 폐암 환자는 200명, 정상인은 800명, 흡연자는 300명, 비흡연자는 700명이라는 사실이 변하지 않는다고 가정하고 논의를 이어갔다. 여기에서 만약 (A)가 100이라면 (B), (C), (D)의 값은 바로 100, 200, 600으로 정해진다. 우리가 "자유"로이 정할 수 있는 값은 (A), (B), (C), (D)중 단 한 개일 뿐이다. 따라서 자유도는 1이 된다.

자유도를 구하는 공식은 왜 $\left(열의\ 개수 - 1 \right)\times\left(행의\ 개수 - 1 \right)$인가?

 각 영역의 총합은 정해져 있으므로 "초등학교 졸업"영역에서 자유로이 정할 수 있는 것은 (A), (B), (C)중 두 개 뿐이다. 두 개의 값을 정하면 나머지 하나는 자연스럽게 정해지기 때문이다. 여기에서는 (A), (B)를 자유롭게 정했다고 하자.

 저체중 영역에서도 (A), (D), (G), (J) 중 세 개만 자유롭게 정할 수 있는데 (A), (D), (G)를 자유로이 정했다고 하자. 같은 방식으로 논리를 전개하면 자유롭게 정할 수 있는 값은 파란 색으로 표시된 6개 뿐이다. 즉, 열의 개수에서 1을 뺀 값과, 행의 개수에서 1을 뺀 값을 곱하여 자유도를 구할 수 있게 된다.

[이론] 카이 제곱 검정 (Chi-squared test) 정복 완료!

작성일: 2022.08.16.

최종 수정일: 2022.08.16.

이용 프로그램: R 4.1.3

RStudio v1.4.1717

RStudio 2021.09.1+372 "Ghost Orchid" Release 

운영체제: Windows 10, Mac OS 10.15.7

[이론] Q-Q Plot (Quantile-Quantile Plot)

정규성을 검정할 때 Q-Q Plot을 쓰곤 한다. 그런데 이런 궁금증이 들 수 있다.

왜 Q-Q Plot이 직선에 가까운 것이 정규성을 따른다는 뜻인가?

이에 대해 조목조목 설명해나갈 것이다.

먼저, 정규성을 따른다는 것이 어떤 의미인지 명확히 이해하고, 명확하게 설명할 수 있어야 한다.

정규성을 따른다는 것이 무엇인가?

정규성을 따른다는 것을 가장 쉽게 말하자면, 이는 히스토그램이 정규분포 곡선과 같이 종모양으로 생겼다는 것을 의미한다.

그렇다면 정규분포 곡선은 무엇을 의미하는가?

[사전 지식: 확률 밀도 함수의 그래프 아래 전체 면적은 1이다.]

어렵게 표현하자면 정규분포곡선은 정규분포의 확률 밀도 함수 (Probability Density Function, PDF)다. 그리고 확률 밀도 함수의 적분 값은 대상의 분율을 의미한다. 이해할 수 있는 언어로 표현하면 다음과 같다. 현실 세계에서 ALT의 분포는 정규분포를 따른다고 가정하자. 이때 아래 그림은 ALT의 분포를 나타낸 것이다. 여기에서 파란색으로 칠한 부분의 면적은 0.84인데 이 말은 전체 인구 중 84%의 ALT가 40 이하라는 뜻이다. 즉 전체 인구가 100명이라면 ALT 작은 순서대로 줄을 세웠을 때 84번째 서있는 사람의 ALT는 40이 된다.

  우리가 연구를 할 때 인구 전체를 대상으로 할 수는 없고 일부를 표본으로 뽑을 수밖에 없다. 설명을 용이하게 하기 위해 간단한 상황으로 전체 인구 중 3명을 뽑는 상황을 가정해보자. 누군가 ALT가 높거나 낮은 사람이 잘 뽑히도록 조작을 하지 않는 한 평균 정도에 있는 사람이 한 명, 평균 이하인 사람 중 한 명, 평균 이상인 사람 중 한 명이 뽑힐 것이라고 생각하는 것이 상식적이다. 

 위 그래프는 평균을 기준으로 대칭이므로 종 모양의 가장 높은 곳에 평균이 위치한다. 또한, 확률 밀도 함수 곡선 아래 면적은 1과 같으므로 아래 보라색 영역의 면적은 0.5와 같다. (평균은 35.1이다.)

 평균 이하인 사람 중 한 명은 어디에서 고르는 것이 합리적일까? 당연히 중간이다. 그런데 중간이 어디인지 어떻게 아는가? ALT의 최솟값이 19, 평균이 35이므로 두 값의 정중앙인 27로 골라야 하는가? 아니다. 평균 이하인 사람이 50명이라면 순서대로 줄을 세운 뒤 정중앙인 25번째에 서있는 사람을 골라야 한다. 줄을 세운 뒤 몇 등인지 확인하는 것은 정규분포 곡선 아래 면적을 구하는 것과 같으므로 왼쪽 끝에서부터 적분했을 때 0.25가 되는 ALT값을 찾아야 한다.  즉, 아래 그림에서 초록색 면적이 0.25가 되는 ALT값을 찾아야 한다. (이 ALT 값은 31.7이다)

평균 이상인 사람 중 한 명을 고르는 것도 같은 논리가 적용된다. 곡선 아래 면적이 0.75인 ALT값을 찾아야 한다. 즉, 아래 그림에서 노란색 면적이 0.75가 되는 ALT값을 찾아야 한다. (이 ALT 값은 38.5이다)

따라서 전체 인구 중 3명을 뽑았는데 그 ALT값이 각각 31.7, 35.1, 38.5였다면 정규분포를 따른다고 생각할 수 있다. (물론 이 예시는 3명이므로 당연히 정규분포를 따른다고 결론 내리는 것이 매우 부적절하다. 하지만 n수가 많다면 타당한 논리일 수 있다.) 

거꾸로 생각해보기

 그렇다면 위의 사전 지식이 없을 때 3명의 ALT 값이 각각 31.7, 35.1, 38.5였다면 이 값들이 정규분포를 따르는지 어떻게 확인할 수 있을까? 위의 과정을 그대로 거꾸로 쫓아가면 된다.

1) 데이터 줄세우고 상대적 위치 확인하기

ALT 값을 작은 순서대로 줄 세우면 31.7, 35.1, 38.5와 같다. 가장 작은 ALT값의 위치를 0, 가장 큰 ALT값의 위치를 1이라고 가정하면 중간의 35.1은 0.5에 위치한다고 볼 수 있고, 작은 값인 31.7은 0.25에 위치한다고 볼 수 있고, 큰 값인 38.5는 0.75에 위치한다고 볼 수 있다. 즉, 전체 인구가 100명이고 ALT가 정규분포를 따른다고 가정했을 때, 만약 25등의 ALT값이 31.7, 50등의 ALT값이 35.1, 75등의 ALT값이 38.5라면 3명의 데이터는 정규분포를 따른다고 생각할 수 있다.

2) 25등, 50등, 75등의 ALT값 확인하기

ALT의 평균은 35.1, 표준편차는 5.0이다. 그렇다면 평균이 35.1, 표준편차가 5.0인 정규분포 곡선을 그리고 왼쪽 끝에서부터 적분했을 때, 넓이가 0.25, 0.5, 0.75가 되는 ALT 값을 찾으면 된다. 그 값은 31.7, 35.1, 38.5이다. 이 위치는 정규분포를 따른다면 이론적으로 3명의 데이터가 위치해야 하는 곳을 의미한다.

3) [표본 3명의 ALT값]과 위에서 구한 [25등, 50등, 75등의 ALT값]을 비교하기

표본 3명의 ALT값은 31.7, 35.1, 38.5이고, 25등, 50등, 75등의 ALT값 이론적으로  31.7, 35.1, 38.5에 위치해야 한다. 실제 표본의 ALT값과 이론적인 값을 순서쌍으로 만들면 (31.7, 31.7), (35.1,35.1), (38.5, 38.5)다. 이를 좌표평면에 나타내면 일직선상에 존재하게 된다.

4) ALT의 평균과 표준편차를 모르는데?

 일반적으로, 우리가 표본을 뽑아 연구하는 이유는 모집단 전체를 대상으로 연구하기엔 시간과 돈이 많이 소비되기 때문이다. 따라서 모집단의 ALT 평균과 표준편차를 알 리가 없다. 이미 알고 있다면 연구할 필요가 없다. 이럴 때 어떻게 할 수 있을까? 평균이 0, 표준편차가 1인 표준 정규분포를 이용하면 된다. 표준 정규분포 곡선을 왼쪽 끝에서부터 적분했을 때, 넓이가 0.25, 0.5, 0.75가 되는 Z값을 찾으면 된다. 그 값은 각각 -0.67, 0, 0.67이다.

만약 모집단의 평균과 표준편차를 알고 있다면 다음 수식을 통해 이론적인 ALT 값(X)을 구할 수 있다.

$$Z=\frac{X-\mu}{\sigma}$$

 하지만, 정규성을 따지는데 굳이 이론적인 값까지 알 필요는 없다. 정규성을 따른다면 실제 값과 이론적인 값(X)이 일직선상에 존재한다는 것은 이미 위에서 밝혔다. 그런데 위 수식에 의거 이론적인 값(X)은 Z와 선형 관계에 있다. 따라서 실제 값 또한 Z와 선형 관계에 있다. 따라서 정규성을 따른다면 실제 값은 Z와 선형 관계를 띄기 때문에 일직선 상에 위치하게 된다. 이 점에 착안하여 실제 값과 Z의 plot을 그린 것이 Q-Q plot이다.

 또한 가로축에 Z, 세로축에 X를 놓는다면, 당연하게도 기울기는 $\sigma$가 된다.

실제 Q-Q plot 그릴 때 다를 수 있는 점

 여기까지 읽어본 독자 중 누군가는 Q-Q plot을 직접 그려보았을 수도 있다. (그리는 법은 다음 링크 참고:2022.08.11 - [기술 통계/R] - [R] 정규성 검정 (1) : QQplot - qqnorm(), qqline()) 그러면 위와 다른 그림을 그려주는 것을 확인할 수 있다.

코드

qq<-qqnorm(c(31.7, 35.1, 38.5))
identity(qq)

결과

$x
[1] -0.8694238  0.0000000  0.8694238

$y
[1] 31.7 35.1 38.5

x축 위치가 (-0.67, 0, 0.67)이 아니다! 왜 이런 일이 발생한 것일까?

필자는 3명의 상대적 위치를 0.25, 0.5, 0.75로 잡았다. 하지만 상대적 위치를 어디로 잡는 것이 좋은가에 대해서는 갑론을박이 있을 수 있으며 많은 방법론이 다음 표와 같이 존재한다. 필자는 이해를 돕기 위해 가장 간단한 첫 번째 방법 (Van der Waerden)을 사용하였다.

R에서는 n수가 10 이하일 때까지는 Blom의 방법을, 11부터는 Rankit의 방법을 사용한다. 

SPSS, R에서는 각각의 방법에 따라 Q-Q plot을 그릴 수 있다. 다음 링크에서 확인할 수 있다.

SPSS:

R:

[이론] Q-Q plot 정복 완료!

작성일: 2022.08.12.

최종 수정일: 2022.08.12.

이용 프로그램: R 4.1.3, RStudio v1.4.1717

운영체제: Windows 10