의학 통계 코드 저장소

[SAS] 편상관 계수, 부분 상관 계수 (Partial correlation coefficient) - PROC CORR

세상의 많은 지표들은 서로 상관되어있는 경우가 많다. 비흡연자에 비해 흡연자가 폐암에 잘 걸리고, 부모의 키가 클수록 아이의 키도 크다. 소득 수준이 높은 나라일수록 평균 수명도 길고, 수학 점수가 높은 학생은 물리 점수가 높으며, 식당에서 음식을 많이 시킬수록 계산해야 하는 금액도 커진다. 변수의 형태에 따라 피어슨 상관 계수 (Pearson's correlation coefficient)를 구하거나 스피어만 상관 계수 (Spearman's correlation coefficient), 혹은 켄달의 타우 (Kendall's tau)를 구하기도 한다. 관련 내용은 다음 링크에서 확인할 수 있다.

2023.04.10 - [상관분석/SAS] - [SAS] 피어슨 상관 계수 (Pearson's correlation coefficient) - PROC CORR ()

2023.04.10 - [상관분석/SAS] - [SAS] 스피어만 상관 계수, 켄달의 타우 (Spearman's rank correlation coefficient, Kendall's tau) - PROC CORR

 그런데 만약 다음과 같은 상황이라면 어떨까?

목표: 수축기 혈압이 심혈관 질환 위험에 미치는 영향을 알아보고자 한다. 

상황: 수축기 혈압이 높은 사람은 일반적으로 BMI도 높다. 그런데, 높은  BMI는 심혈관 질환의 위험 인자다.

문제: 높아진 심혈관 질환 위험이 수축기 혈압 때문인지, BMI 때문인지 구분할 수가 없다.

 이런 상황에서 BMI를 교란 요인 (confounding factor, confounding variable, confounder)이라고 하며, 교란요인의 영향을 보정하는 것은 의학 통계 전반에 있어서 아주 중요한 문제다. 

 상관 계수 (correlation coefficient)를 구할 때 교란 변수를 보정하는 방법은 편상관 계수 혹은 부분 상관 계수(partial correlation coefficient)를 구하는 것이다. 이에 대해서 알아보도록 하겠다.

*실습용 데이터는 아래 링크를 클릭하면 다운로드할 수 있습니다.

2022.08.04 - [공지사항 및 소개] - 분석용 데이터 (update 22.12.18)

시작하기 위해 라이브러리를 만들고, 파일을 불러온다.

라이브러리 만드는 방법: 2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 라이브러리 만들기 - LIBNAME

파일 불러오는 방법: 2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 데이터 불러오기 및 저장하기 - PROC IMPORT, PROC EXPORT

*라이브러리 지정하기;
LIBNAME hong "C:/Users/User/Documents/Tistory_blog";

*파일 불러오기;
PROC IMPORT
DATAFILE="C:\Users\user\Documents\Tistory_blog\Data.xlsx"
DBMS=EXCEL
OUT=hong.df
REPLACE;
RUN;

목표:  BMI의 영향을 배제 혹은 교정하고도 수축기 혈압은 심혈관 질환 위험과 상관 관계를 갖는가?

코드 - 일반적인 피어슨 상관 계수 구하기

먼저 수축기 혈압과 심혈관 질환 위험 간의 상관 계수를 구해보자. 이는 이전 포스팅에서 다룬 PROC CORR 함수를 사용하면 된다.

2023.04.10 - [상관분석/SAS] - [SAS] 피어슨 상관 계수 (Pearson's correlation coefficient) - PROC CORR

PROC CORR DATA=hong.df;
VAR SBP CVD_RISK;
RUN;

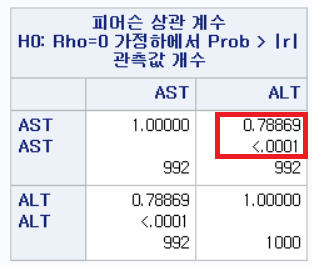
결과

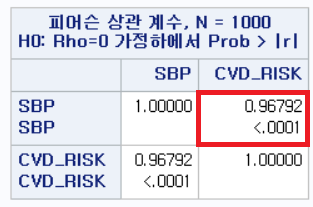
상관 계수가 0.96792로 매우 높다. 

그렇다면, BMI의 영향을 배제하는 코드는 어떻게 될까?

코드 - 편상관 계수 / 부분 상관 계수

PROC CORR DATA=hong.df;
VAR SBP CVD_RISK;
PARTIAL BMI;
RUN;

PROC CORR DATA=hong.df; : 상관계수를 구하는 작업을 시작하되, 데이터는 hong라이브러리의 df를 사용하라.
VAR SBP CVD_RISK; : SBP와 CVD_RISK간의 상관계수를 구하라
PARTIAL BMI; : 근데, BMI의 영향은 배제시킨 편상관 계수 / 부분 상관 계수를 구하라.

결과

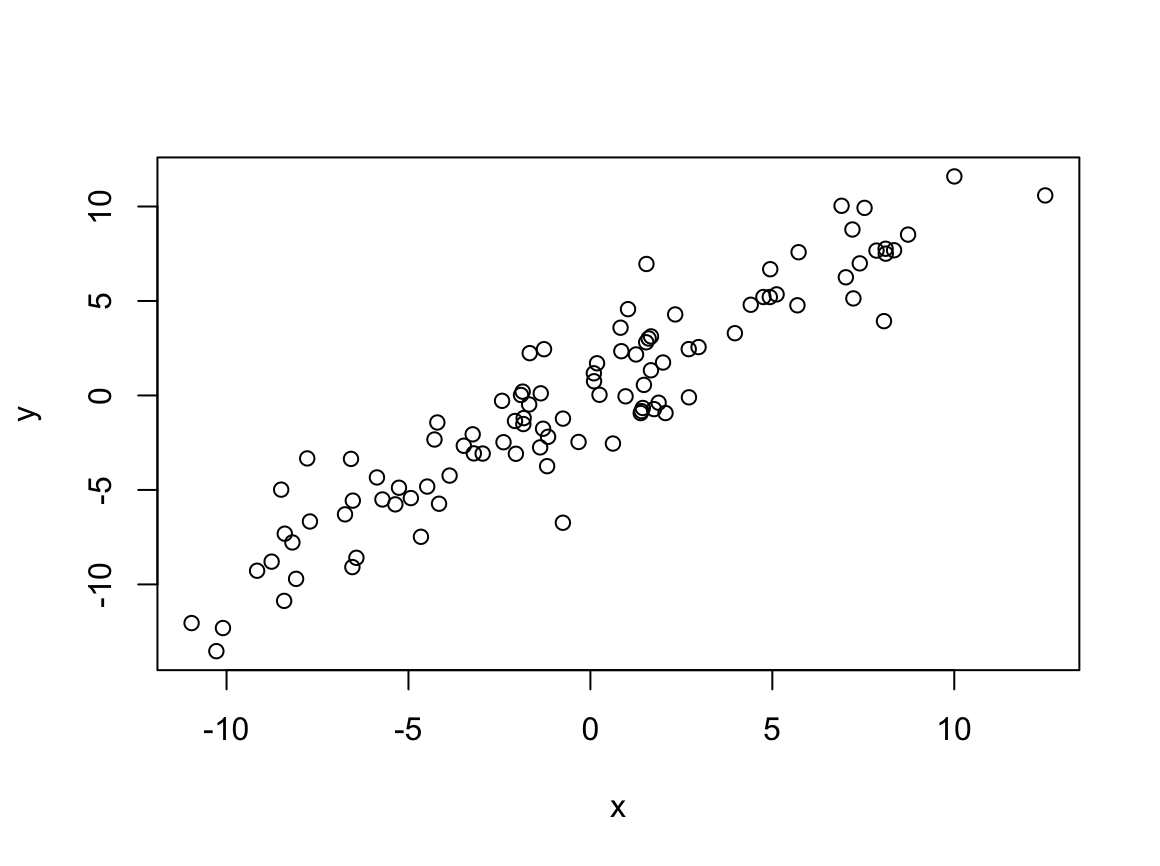
BMI로 보정하면, SBP와 CVD_RISK사이의 상관 계수는 0.85242로 보정하기 전의 0.96792보다는 소폭 감소한 모양이다. BMI가 CVD_RISK를 증가시키는 설명력을 배제하였기 때문이다. 이때의 p-value는 0.0001보다 작으므로 0이 아니라는 대립 가설을 택할 수 있다. 

두 개 이상의 교란 변수를 보정

만약, 두 개 이상의 교란 변수를 보정하고자 한다면 보정할 변수들을 list로 만들어 넣으면 된다. BMI뿐만 아니라 흡연력인 SMOK도 보정변수로 넣고 싶다면 다음과 같은 코드를 쓰면 된다. (SMOK는 순서형 변수이므로 Pearson이 적절하지 않으므로 Spearman이나 Kendall 사이에서 골라야 하는데, 같은 값을 갖는 사람(tie)이 많으므로 Kendall의 tau를 구하도록 한다.)

PROC CORR DATA=hong.df KENDALL;
VAR SBP CVD_RISK;
PARTIAL BMI SMOK;
RUN;

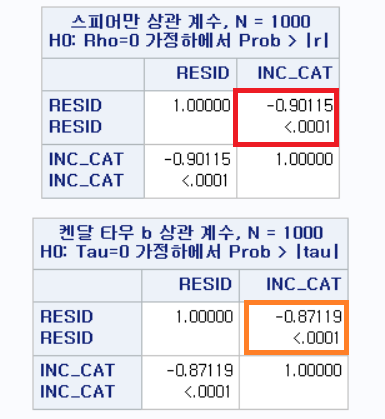
결과

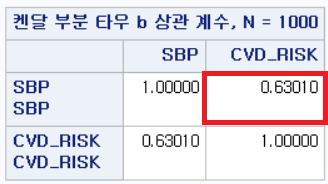
결과에 p-value가 제시되지 않는다. SAS 로그창에는 다음과 같이 언급된다: 

NOTE: 켄달의 부분 타우-b 에 대한 확률값을 이용할 수 없습니다.

이는 당연하다. SAS의 PROC CORR 다큐먼트에 의하면 다음과 같이 쓰여있다. 

 If you use a PARTIAL statement, probability values for Kendall’s partial tau-b are not available.

이에 대해 이 방법론의 개발자인 Kendall은 "p-value를 구할 수 있는 방법이 없다." 라고 언급하고 있다. (출처: Goodman, Leo A. "Partial tests for partial taus." Biometrika 46.3/4 (1959): 425-432.)

그런데, 같은 내용을 다룬 R에서는 p-value를 제시하고 있다. 2022.12.18 - [상관분석/R] - [R] 편상관 계수, 부분 상관 계수 (Partial correlation coefficient) - pcor.test() 그 사이 무슨 특별한 방법이라도 개발된 것일까? 당연히 그렇지 않은 것으로 보인다. R에서 제시하는 Kendall's partial tau의 p-value는 일반 Kendall's tau의 p-value와 같은 방법으로 구하고 있는 것으로 보인다. 쌍이 50개 미만이고, tie가 없다면 exact p-value를 구해주고. 그 이상이라면 정규분포를 따른다고 생각되는 통계량을 구한 뒤 그에 대한 p-value를 제시한다. 

얼마나 높아야 높다고 할 수 있는가?

상관계수가 "얼마나 높아야 높다고 할 수 있는가?"라는 의문이 들 수 있다. 즉, "how high is high?"라는 질문에 대한 답은 사실 정해져 있진 않다. 연구자마다 기준은 다른데, 그중 한 가지는 다음과 같다.

코드 정리

*라이브러리 지정하기;
LIBNAME hong "C:/Users/User/Documents/Tistory_blog";

*파일 불러오기;
PROC IMPORT
DATAFILE="C:\Users\user\Documents\Tistory_blog\Data.xlsx"
DBMS=EXCEL
OUT=hong.df
REPLACE;
RUN;

*편상관계수 구하기;
PROC CORR DATA=hong.df;
VAR SBP CVD_RISK;
PARTIAL BMI;
RUN;

*두 변수로 보정한 편상관계수(Kendall) 구하기;
PROC CORR DATA=hong.df KENDALL;
VAR SBP CVD_RISK;
PARTIAL BMI SMOK;
RUN;

[SAS] 편상관 계수, 부분 상관 계수 (Partial correlation coefficient) 정복 완료!

작성일: 2023.04.20.

최종 수정일: 2023.10.17.

이용 프로그램: SAS v9.4

운영체제: Windows 11

[R] 스피어만 상관 계수, 켄달의 타우 (Spearman's rank correlation coefficient, Kendall's tau) - cor.test()

 세상의 많은 지표들은 서로 상관되어 있는 경우가 많다. 비흡연자에 비해 흡연자가 폐암에 잘 걸리고, 부모의 키가 클수록 아이의 키도 크다. 소득 수준이 높은 나라일수록 평균 수명도 길고, 수학 점수가 높은 학생은 물리 점수가 높으며, 식당에서 음식을 많이 시킬수록 계산해야 하는 금액도 커진다.

 그런데, 세상만사 칼같이 딱딱 떨어지는 게 아니다. 폐암에 걸리지 않는 꼴초도 있는가 하면, 부모의 키는 크지만 아이의 키는 작을 수 있다. 수학만 잘하고 물리는 못 할 수도 있다. 이렇게 예외가 있는 관계가 있는가 하면, 예외가 있을 수 없는 관계도 있다. $10,000$원짜리 삼겹살을 $x$인분 시키면 계산해야 하는 금액은 반드시 $10,000x$가 되는 게 일례가 될 수 있다. 

 예외가 많은 부모와 자녀의 키 문제로 돌아가 보자. 부모의 키로 자녀의 키를 유추하면 틀리는 경우가 많이 생기게 된다. 다시 말해, 불확실성이 높아진다. 반대로 삼겹살 주문량으로 예측한 계산 금액은 틀릴 수가 없다. 우리는 얼마나 정확하게 예측할 수 있는지를 계량하고자 한다. 그 방법 중 하나로, 두 변수가 연속 변수일 때 사용하는 피어슨 상관 계수 (Pearson's correlation coefficient)가 있다. 이는 이전 포스팅에서 다루었다. 2023.04.10 - [상관분석/SAS] - [SAS] 피어슨 상관 계수 (Pearson's correlation coefficient) - PROC CORR ()

 하지만 세상 모든 변수가 연속형 변수는 아니다. "월 수입이 얼마입니까?"라는 설문에 주관식으로 "_____만원"으로 답했다면 이는 연속변수일 것이다. 하지만 "월 수입이 다음 중 어디에 속하십니까?"라는 설문에 대해 다음과 같은 객관식으로 답을 하게 되어있다면 이는 연속형 변수가 아닌 순위형 변수가 될 것이다.

 1) 100만 원 미만

 2) 100만 원 이상 300만 원 미만

 3) 300만 원 이상 700만 원 미만

 4) 700만 원 이상 1,500만 원 미만

 5) 1,500만 원 이상

 월 소득 50만원인 사람 A에게는 1이란 값이 부여될 것이고, 월 소득 1,700만 원인 사람 B에게는 5라는 값이 부여될 것이다. 부여된 1과 5의 평균을 구하는 것이 의미가 있을까? 만약 의미가 있다고 치고 구해보면 1과 5의 평균은 3이다. 따라서 평균 소득은 300만 원 이상 700만 원 미만일 것이라고 예측할 수 있는데, 사실  이 두 명의 평균 소득은 875만 원이므로 4번 구간에 속한다. 이런 차이가 발생하게 되므로, 점수 같은 연속형 변수 값 자체가 아니라 석차와 같은 순위형 변수의 상관관계를 보고 싶을 때에는 피어슨 상관 계수를 사용할 수 없다. 왜냐하면 피어슨 상관 계수는 평균, 표준편차, 공분산을 사용하기 때문이다. 대신에 스피어만 상관 계수 (Spearman's rank correlation coefficient)나 켄달의 타우 (Kendall's tau)를 사용해야 한다. 

스피어만 상관 계수 (Spearman's rank correlation coefficient - 주로 rho로 나타낸다.)나 켄달의 타우 (Kendall's tau)는 두 변수 사이의 상관관계의 정도를 나타내는 지표다. 이는 -1과 1 사이의 값을 갖는데 -1 혹은 1에 가까워질수록, 달리 표현하면 상관 계수의 절댓값이 커질수록, 즉 0에서 멀어질수록 "예측할 수 있는 정도"가 높아진다. 1에 가까워지는 것은 양의 상관관계인데 "예측도"가 증가하는 것을 의미하고, -1에 가까워지는 것은 음의 상관관계인데 "예측도"가 증가하는 것을 의미한다. 

*실습용 데이터는 아래 링크를 클릭하면 다운로드할 수 있습니다.

2022.08.04 - [공지사항 및 소개] - 분석용 데이터 (update 22.12.18)

시작하기 위해 라이브러리를 만들고, 파일을 불러온다.

라이브러리 만드는 방법: 2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 라이브러리 만들기 - LIBNAME

파일 불러오는 방법: 2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 데이터 불러오기 및 저장하기 - PROC IMPORT, PROC EXPORT

*라이브러리 지정하기;
LIBNAME hong "C:/Users/User/Documents/Tistory_blog";

*파일 불러오기;
PROC IMPORT
DATAFILE="C:\Users\user\Documents\Tistory_blog\Data.xlsx"
DBMS=EXCEL
OUT=hong.df
REPLACE;
RUN;

목표:  월 수입(순위형 변수)과 거주 지역 단위에는 관계가 있는가?

월 수입 :INC_CAT

0: 하위 3분위

1: 중앙 3분위

2: 상위 3분위

거주 지역 단위: RESID

0: 대도시

1: 중소도시

2: 시골

스피어만 상관 계수와 켄달의 타우를 구하는 코드는 다음과 같다.

코드

PROC CORR DATA=hong.df SPEARMAN KENDALL;
VAR RESID INC_CAT;
RUN;

PROC CORR DATA=hong.df SPEARMAN KENDALL; 상관분석(CORRelation)을 할 것이다. 데이터는 hong 라이브러리의 df 데이터를 사용해라. 구할 지표는 Spearman's rank correlation coefficient와 Kendall의 tau다.
VAR RESID INC_CAT; RESID와 INC_CAT 간의 상관계수를 구하

결과

-중요한 것은 상관계수 -0.90115와 -0.87119이다. -1에 가까울수록 음의 상관관계가 존재함을 나타내는데, 이 정도면 꽤 높은 음의 상관관계가 있다고 할 수 있다.

- 따라서 대도시에 사는 사람일수록 수입이 많다고 할 수 있다.

- p value는 <0.0001로 상당히 작아 매우 유의함을 알 수 있다. 따라서 귀무가설을 기각하고 대립 가설을 택해야 하는데, 이 검정의 귀무가설은 "상관 계수는 0"이라는 것이다. 따라서 상관 계수가 0은 아니라고 결론 내릴 수 있다.

얼마나 높아야 높다고 할 수 있는가?

위에서 0.79 정도면 꽤 높은 상관관계가 있다고 할 수 있다고 했는데, "얼마나 높은 것이 높은 것인가?"라는 의문이 들 수 있다. 즉, "how high is high?"라는 질문에 대한 답은 사실 정해져 있진 않다. 연구자마다 기준은 다른데, 그중 한 가지는 다음과 같다.

둘 중 하나만 순위형 변수인 경우

만약 둘 중 하나만 순위형 변수고 다른 하나는 연속형 변수인 경우 어떻게 해야 할까? 예를 들어, 거주 지역 단위와 대기 중 미세먼지의 양 사이의 상관관계를 구하고자 할 때에도 스피어만 상관 계수 (Spearman's rank correlation coefficient)나 켄달의 타우 (Kendall's tau)를 사용해야 한다. 

스피어만 상관 계수 vs 켄달의 타우

둘 중에 어떤 것을 사용해야 할까?

스피어만 상관 계수는 tie가 없다고 가정한다. 즉, 같은 순위를 갖는 사람이 없는 것이다. 위 예시의 경우 대도시, 중소도시, 시골에 사는 사람이 1명씩은 아니니 스피어만 상관 계수는 적절하지 않다. 이럴 때에는 켄달의 타우가 더 적절하다. 또한, 표본의 수가 적을 때에도 켄달의 타우가 조금 더 적절하다.

[SAS] 스피어만 상관 계수, 켄달의 타우 (Spearman's rank correlation coefficient, Kendall's tau) 정복 완료!

작성일: 2023.04.10.

최종 수정일: 2023.10.17.

이용 프로그램: SAS v9.4

운영체제: Windows 11

[SAS] 피어슨 상관 계수 (Pearson's correlation coefficient) - PROC CORR

 세상의 많은 지표들은 서로 상관되어 있는 경우가 많다. 비흡연자에 비해 흡연자가 폐암에 잘 걸리고, 부모의 키가 클수록 아이의 키도 크다. 소득 수준이 높은 나라일수록 평균 수명도 길고, 수학 점수가 높은 학생은 물리 점수가 높으며, 식당에서 음식을 많이 시킬수록 계산해야 하는 금액도 커진다.

 그런데, 세상만사 칼같이 딱딱 떨어지는 게 아니다. 폐암에 걸리지 않는 꼴초도 있는가 하면, 부모의 키는 크지만 아이의 키는 작을 수 있다. 수학만 잘하고 물리는 못 할 수도 있다. 이렇게 예외가 있는 관계가 있는가 하면, 예외가 있을 수 없는 관계도 있다. $10,000$원짜리 삼겹살을 $x$인분 시키면 계산해야 하는 금액은 반드시 $10,000x$가 되는 게 일례가 될 수 있다. 

 예외가 많은 부모와 자녀의 키 문제로 돌아가 보자. 부모의 키로 자녀의 키를 유추하면 틀리는 경우가 많이 생기게 된다. 다시 말해, 불확실성이 높아진다. 반대로 삼겹살 주문량으로 예측한 계산 금액은 틀릴 수가 없다. 우리는 얼마나 정확하게 예측할 수 있는지를 계량하고자 한다. 그 방법 중 하나가 피어슨 상관 계수 (Pearson's correlation coefficient)다. 

피어슨 상관 계수 (Pearson's correlation coefficient)는 두 변수 사이의 상관관계의 정도를 나타내는 지표다. 이는 -1과 1 사이의 값을 갖는데 -1 혹은 1에 가까워질수록, 달리 표현하면 상관 계수의 절댓값이 커질수록, 즉 0에서 멀어질수록 "예측할 수 있는 정도"가 높아진다. 1에 가까워지는 것은 양의 상관관계인데 "예측도"가 증가하는 것을 의미하고, -1에 가까워지는 것은 음의 상관관계인데 "예측도"가 증가하는 것을 의미한다. 여기에서 예측하는 방법은 선형 방법이다. 즉, 한 변수의 값 $x$를 알 때, 적절한 실수 $a, b$에 대해 $y$값이 $y=ax+b$ 일 것이라고 예측할 수 있다는 것이다. 여기에서 피어슨 상관 계수에 대해 대표적으로 오해하는 점 두 가지를 들 수 있다. 

 1) 피어슨 상관 계수가 크면 기울기($a$값)이 크다. 기울기는 위 삼겹살 예시에서 1인분당 가격을 의미하는 것인데, 1인분 추가 주문 시 증가되는 전체 주문 금액으로 이해할 수 있다. 그런데 피어슨 상관 계수에는 이에 대한 정보가 전혀 없다. 피어슨 상관 계수는 (1) 양의 상관관계인지 음의 상관관계인지, (2) 얼마나 "예측도"가 큰지, 즉 데이터들이 얼마나 직선상에 모여있는지 에 대한 정보만 제공한다. 

 2) 피어슨 상관 계수가 0이면, 두 변수 사이에는 어떠한 상관 관계도 없다. 위에서 설명했듯이, 피어슨 상관 계수는 선형 방법으로 예측할 수 있는 정도를 표현한다. 따라서 선형 관계가 아닌 2차 함수 관계, 사인 함수 관계, 원형 함수 관계 등이 존재한다면, 두 변수 사이의 어떤 관련성은 분명히 존재하는 것이지만, 피어슨 상관 계수는 0일 수 있다. 

 본격적으로 피어슨 상관 계수를 구해보자. 

*실습용 데이터는 아래 링크를 클릭하면 다운로드할 수 있습니다.

2022.08.04 - [공지사항 및 소개] - 분석용 데이터 (update 22.12.18)

시작하기 위해 라이브러리를 만들고, 파일을 불러온다.

라이브러리 만드는 방법: 2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 라이브러리 만들기 - LIBNAME

파일 불러오는 방법: 2022.08.05 - [통계 프로그램 사용 방법/SAS] - [SAS] 데이터 불러오기 및 저장하기 - PROC IMPORT, PROC EXPORT

*라이브러리 지정하기;
LIBNAME hong "C:/Users/User/Documents/Tistory_blog";

*파일 불러오기;
PROC IMPORT
DATAFILE="C:\Users\user\Documents\Tistory_blog\Data.xlsx"
DBMS=EXCEL
OUT=hong.df
REPLACE;
RUN;

목표:  혈중 ALT와 AST에는 선형 상관관계가 존재하는가?

피어슨 상관 계수 (Pearson's correlation coefficient)를 구하는 코드는 다음과 같다.

코드

PROC CORR DATA=hong.df;
VAR AST ALT;
RUN;

PROC CORR DATA=hong.df; : 상관 분석 (CORRelation)을 시행하되 데이터는 hong 라이브러리의 df를 이용하라.
VAR AST ALT; : 변수는 AST와 ALT다. 둘 사이의 상관계수를 구하라.

결과

- 상관계수는 0.78869이다. 1에 가까울수록 양의 상관관계가 존재함을 나타내는데, 0.79 정도면 꽤 높은 "선형" 상관관계가 있다고 할 수 있다.

- 유의확률은 "<0.0001"으로 상당히 작으므로 매우 유의함을 알 수 있다. 따라서 귀무가설을 기각하고 대립 가설을 택해야 하는데, 이 검정의 귀무가설은 "상관 계수는 0"이라는 것이다. 따라서 상관 계수가 0은 아니라고 결론 내릴 수 있다.

얼마나 높아야 높다고 할 수 있는가?

위에서 0.79 정도면 꽤 높은 상관관계가 있다고 할 수 있다고 했는데, "얼마나 높은 것이 높은 것인가?"라는 의문이 들 수 있다. 즉, "how high is high?"라는 질문에 대한 답은 사실 정해져 있진 않다. 연구자마다 기준은 다른데, 그중 한 가지는 다음과 같다.

피어슨 상관 계수 산출의 가정

 피어슨 상관 계수를 산출할 때, 기본적으로 가정은 존재하지 않는다. 수학적으로 표현하면 공분산을 각각의 표준 편차로 나눠준 것이니, 어떠한 가정도 필요하지 않다. 다만 해석에 유의해야 한다. 피어슨 상관 계수가 1 또는 -1에 가까운 값이 나왔을 때의 해석은 어디까지나 "선형 상관관계가 있다."는 것이다. 심지어 1에 가까운 값이더라도, 선형 상관관계보다 두 변수 사이의 관계를 더 잘 표현하는 관계가 있을 수 있다. 예를 들어, 어떤 변수 x와 y의 피어슨 상관 계수는 0.89로 매우 높은데, 둘 사이의 그래프는  아래와 같이 그려진다고 하자.

둘 사이의 상관 계수가 1(완벽한 선형 예측이 가능)은 아니지만, x와 y사이에는 이차 함수의 관계가 있는 것으로 보인다. "예측도"측면에서 상관 계수가 1은 아니므로 선형 예측은 완벽하지 않지만, 이차 함수의 관계로 보면 완벽하게 예측할 수 있는 관계다. 

또한, 피어슨 상관 계수가 0에 가까운 값이 나왔을 때의 해석은 어디까지나 "선형 상관관계가 없다."는 것이다.  예를 들어 상관계수가 0인 다음 두 변수 x와 y의 그래프는 다음과 같이 그려진다고 한다.

"예측도"측면에서 상관 계수가 0이므로 선형 예측이 불가능해야 하지만, 이차 함수의 관계로 보면 완벽하게 예측할 수 있는 관계다. 따라서 피어슨 상관 계수를 "예측도", "관련성"이라는 의미로 사용하려 한다면, 두 변수 사이의 산점도를 꼭 그려보는 것이 좋다.

두 변수 사이의 산점도 (플롯) 그리기.

산점도를 그리기위해서는 상관 계수를 구하는 코드에 한 마디만 추가하면 된다.

PROC CORR DATA=hong.df PLOTS=SCATTER;
VAR AST ALT;
RUN;

"PLOTS=SCATTER"라는 문구 하나를 추가하면 다음과 같은 산점도를 그려준다.

둘 사이에는 어떤 선형 관계가 있어 보인다. 그렇다면 우리가 산출한 피어슨 상관 계수는 AST와 ALT의 관련성을 잘 나타낸다고 할 수 있다. 즉, 이차 함수 관계 등 다른 비선형적 관계가 있는데도 불구하고 우리가 선형 상관 계수를 구해서 1보다 낮은 값이 나온 것이 아니라, 원래 선형 관계인데 어느 정도의 불확실성 때문에 1보다는 낮은 값이 나온 것이라고 결론지을 수 있다. 따라서 산점도를 꼭 그려보고 어떠한 관계 속에 있는지 확인하고 상관 계수를 해석하는 것은 매우 중요하다. 

가정이 정말 없는가?

 가정이 필요하다는 글, 책들이 정말 많을 것이다. 그럼에도 불구하고 나는 가정이 필요 없다는 말을 계속해왔다. 정말 가정이 없는 것일까? 답은 "그렇다"이다. 정말 없다. 하지만, Pearson's correlation coefficient가 적절할 때, 적절하지 않을 때는 분명히 존재한다. 피어슨 상관 계수는 두 변수가 연속형 변수일 때 좋다. 그리고 이상치(outlier)가 없을 때 정말 좋다. 이상치(outlier)는 피어슨 상관 계수의 값을 크게 변화시킬 수 있으며, 특히 표본의 수가 많지 않을 때 이런 일은 더 빈번하게 나타날 수 있다. 이럴 때에는 스피어만 상관 계수 (Spearman correlation coefficient)나 켄달의 타우 (Kendall's tau)가 더 적절할 수 있다. 이 두 가지 방식은 특히 순서형 변수일 때 더 큰 효용성을 갖는다. 

 아마도 위와 같은 이유로 피어슨 상관 계수 (Pearson's correlation coefficient)의 전제조건으로 정규성을 많이 이야기하는지도 모른다. 정규성을 따른다면 적어도 이상치로부터 어느 정도 자유로울 수 있고, 왜곡된 상관 계수가 산출되지 않을 수 있다.

[SAS] 피어슨 상관 계수 (Pearson's correlation coefficient) 정복 완료!

작성일: 2023.04.10.

최종 수정일: 2023.10.17.

이용 프로그램: SAS v9.4

운영체제: Windows 11